高中数学选修2-2公开课课件1_5_3 定积分的概念 32页

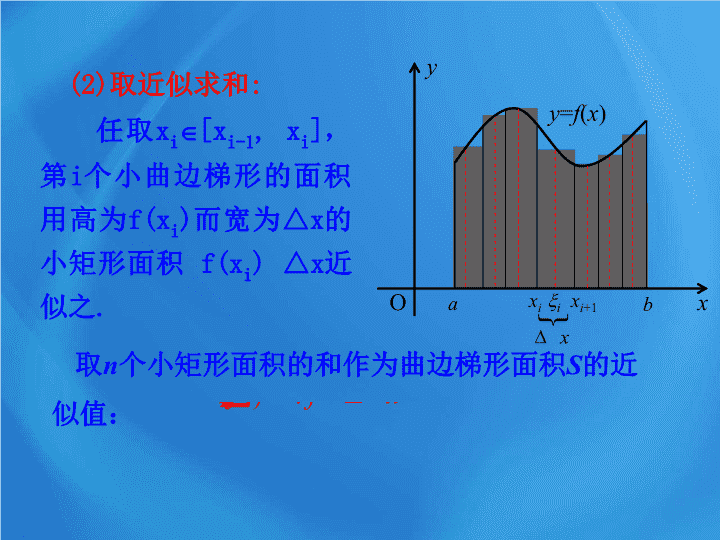
1.5.3 定积分的概念 求曲线 y = f ( x ) 对应的曲边梯形面积的方法 x i y = f ( x ) x y O b a x i +1 x i (1) 分割 : 在区间 [a,b] 上等间隔地插入 n-1 个点 , 将 它等分成 n 个小区间 : 每个小区间宽度 △ x (2) 取近似求和 : 任取 x i  [x i-1 , x i ] ，第 i 个小曲边梯形的面积用高为 f(x i ) 而宽为 △ x 的小矩形面积 f(x i ) △ x 近似之 . x i y = f ( x ) x y O b a x i +1 x i 取 n 个小矩形面积的和作为曲边梯形面积 S 的近似值： (3) 取极限 : 所求曲边梯形的面积 S 为 x i y = f ( x ) x y O b a x i +1 x i 1. 定积分的计算和简单应用 . ( 重点 ) 2. 利用定积分求平面区域围成的面积 . ( 难点 ) 探究点 1 定积分的定义 从求曲边梯形面积 S 的过程中可以看出 , 通过以下四步 : 分割 —— 近似代替 —— 求和 —— 取极限 得到解决 . 定积分的定义 定积分的定义的理解 : 定积分的相关名称：  ——— 叫做积分号， f(x) —— 叫做被积函数， f(x)dx — 叫做被积式， x ——— 叫做积分变量， a ——— 叫做积分下限， b ——— 叫做积分上限， [a, b] — 叫做积分区间 . 被积函数 被积式 积分变量 积分下限 积分上限 O x y a b y  f ( x ) 按定积分的几何意义，有 (1) 由连续曲线 y=f(x) (f(x)  0) ，直线 x=a 、 x=b 及 x 轴所围成的曲边梯形的面积为 (2) 设物体运动的速度 v=v(t) ，则此物体在时间区间 [a, b] 内运动的距离 s 为 1 x y O f(x) = x 2 根据定积分的定义，右边图形的面积为 同样地， 1.5.2 中汽车在 0≤t≤1 这段时间内经过的路程 (1) 定积分是一个数值 , 它只与被积函数及积分区间有关，而与积分变量的记法无关，即 总结提升： (2) 定义中区间的分法和  i 的取法是任意的 . x y O 当 f(x)  0 时，由 y  f (x) 、 x  a 、 x  b 与 x 轴所围成的曲边梯形位于 x 轴的下方， a b y  f ( x ) y  - f ( x ) =- S a b y  f ( x ) O x y 根据定积分的几何意义 , 如何用定积分表示图中蓝色阴影部分的面积 ? b y  f ( x ) O x y 探究点 3 用定积分表示图中阴影部分的面积 a 探究点 4 定积分的基本性质 性质 1 性质 2 (k 为常数 ) 性质 3. 定积分关于积分区间具有 可加性 O x y a b y  f ( x ) Ｃ ( 其中 a ＜ c ＜ b) 性质 3 不论 a ， b ， c 的相对位置如何都有 a b y = f ( x ) c O x y 1. 用定积分表示图中四个阴影部分面积 解： 0 a y x f(x)=x 2 0 x y x -1 2 f(x)=x 2 x -1 0 y x a b f(x)=1 0 y x -1 2 f(x)=(x-1) 2 -1 解： x y f(x)=sinx 1 -1 2. 3. 面积值为圆的面积的 1. 求曲边梯形面积 分割 —— 近似代替 —— 求和 —— 取极限 2. 定积分定义 3. 定积分几何意义 4. 定积分计算性质 健康身体是基础，良好学风是条件，勤奋刻苦是前提，学习方法是关键，心理素质是保证 .