云南省昆明市第一中学2020届高三第八次考前适应性训练数学（理）试题 13页

云南省昆明市第一中学2020届高三第八次考前适应性训练 数学（理）试题 一、选择题:本题共12小题，每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。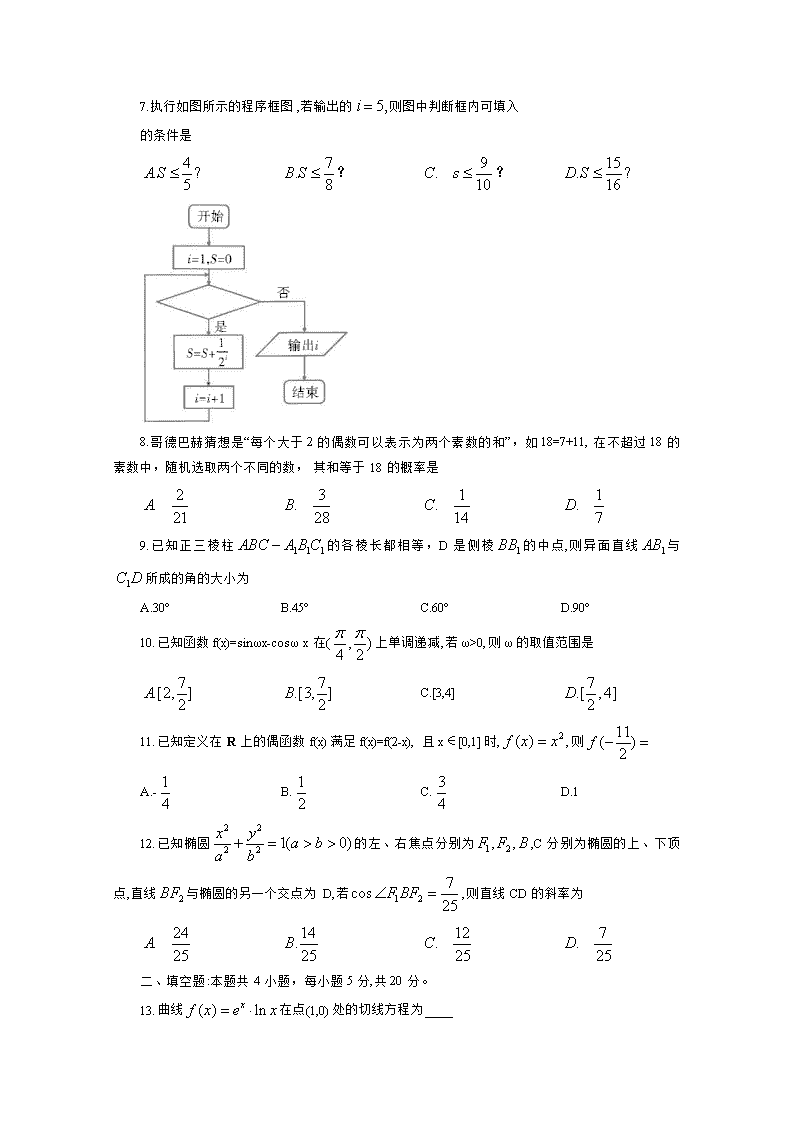‎ ‎1.欧拉公式(其中i为虚数单位)是由著名数学家欧拉发现的,当x=π时,这是数学里最令人着迷的一个公式，数学家们评价它是“上帝创造的公式”.根据欧拉公式，若将所表示的复数记为z,则 ‎ ‎ ‎2.已知集合A={x||x|<3,x∈N},集合B={-1,0,1,2},则图中阴影部分所表示的集合为 A.{1,2} B.{0,1,2} C.{-1,1,2} D.{-1,0,1,2}‎ ‎3.函数的大致图象是 ‎4.已知向量，且与共线,则在方向上的投影为 ‎ ‎ ‎5.已知点在双曲线的渐近线上，则该双曲线的离心率为 ‎ B‎.2 ‎ C.3 D.4‎ ‎6.△ABC的三个内角A,B,C所对的边分别为a,b,c,若则 A.1 D.2‎ ‎7.执行如图所示的程序框图,若输出的则图中判断框内可填入 的条件是 ‎ ？ ？ ‎ ‎8.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如18=7+11,在不超过18的素数中，随机选取两个不同的数，其和等于18的概率是 ‎ ‎ ‎9.已知正三棱柱的各棱长都相等，D是侧棱的中点,则异面直线与所成的角的大小为 A.30° B.45° C.60° D.90°‎ ‎10.已知函数f(x)=sinωx-cosωx在(上单调递减,若ω>0,则ω的取值范围是 ‎ C.[3,4] ‎ ‎11.已知定义在R上的偶函数f(x)满足f(x)=f(2-x),且x∈[0,1]时,则 A.- B. C. D.1‎ ‎12.已知椭圆的左、右焦点分别为,C分别为椭圆的上、下顶点,直线与椭圆的另一个交点为D,若则直线CD的斜率为 ‎ ‎ 二、填空题:本题共4小题，每小题5分,共20分。‎ ‎13.曲线在点(1,0)处的切线方程为____‎ ‎14.若直线kx-y+k=0与不等式组表示的平面区域有公共点，则实数k的取值范围是_____‎ ‎15.已知且θ∈(0,π),则____‎ ‎16.在三棱锥A-BCD中,AB=AC,DB=DC,AB+BD=4,AB⊥BD,则三棱锥A-BCD的外接球体积的最小值为____‎ 三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎(一)必考题:共60分 ‎17.(12分)‎ 已知数列{满足 ‎(1)求的通项公式;‎ ‎(2)求的前n项和 ‎18.(12分)‎ 某厂生产不同规格的一种产品，根据检测标准，其合格产品的质量y(g)与尺寸x(mm)之间近似满足关系式c为大于0的常数).按照某项指标测定，当产品质量与尺寸的比在区间内时为优等品.现随机抽取6件合格产品,测得数据如下:‎ ‎（1）现从抽取的6件合格产品中再任选3件，记ξ为取到优等品的件数，试求随机变量ξ的分布列和期望；‎ ‎（2）根据测得数据作了初步处理，得相关统计量的值如下表：‎ 根据所给统计量,求y关于x的回归方程;‎ 附:对于样本(,其回归直线u=b·v+a的斜率和截距的最小二乘估计公式分别为:‎ ‎19.(12分)‎ 如图,三棱柱的底面是等边三角形在底面ABC上的射影为△ABC的重心G.‎ ‎(1)已知证明:平面平面；‎ ‎(2)已知平面与平面ABC所成的二面角为60°,G到直线AB的距离为a,求锐二面角的余弦值.‎ ‎20.(12分)‎ 已知点F(0,1),直线l:y=-1,点E为l上一动点,过E作直线为EF的中垂线与交于点G,设点G的轨迹为曲线Γ.‎ ‎(1)求曲线Γ的方程;‎ ‎(2)若过F的直线与Γ交于A,B两点,线段AB的垂直平分线交y轴于点P,求|FP|与|AB|的比值.‎ ‎21.(12分)‎ 已知函数f(x)=ln(1+x)+sinx-ax,a>0.‎ ‎(1)当a=2时,证明:f(x)≤0;‎ ‎(2)若f(x)在(-1,+∞)只有一个零点,求a.‎ ‎(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ ‎22.(选修4-4:坐标系与参数方程](10分)‎ 以直角坐标系的原点O为极点,x轴的非负半轴为极轴,建立极坐标系，并在两种坐标系中取相同的长度单位.已知圆和圆的极坐标方程分别是ρ=4cosθ和ρ=2sinθ.‎ ‎(1)求圆和圆的公共弦所在直线的直角坐标方程;‎ ‎(2)若射线OM:θ=α与圆的交点为O、P,与圆的交点为O、Q,求|OP|·|OQ|的最大值.‎ ‎23.[选修4-5:不等式选讲](10分)‎ 已知a,b,c分别是△ABC的三个内角A,B,C的对边.‎ ‎(1)若a,b,c成等比数列，证明:；‎ ‎(2)若a+b<‎2c,证明:c ‎2020届昆一中高三联考卷第八期联考 理科数学参考答案及评分标准 命题、审题组教师 杨昆华 张宇甜 顾先成 李春宣 王海泉 莫利琴 蔺书琴 张远雄 崔锦 杨耕耘 一、选择题 ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 C B A D B D C A D B A C ‎1. 解析：依题意，则，选C.‎ ‎2. 解析：，易知图中阴影部分对应的集合为，，选B.‎ ‎3. 解析：函数为非奇非偶函数，排除B，C选项；当时，，所以选A.‎ ‎4. 解析：由已知：与共线，可得，所以在方向上的投影为：，‎ 选D.‎ ‎5. 解析：因为， 所以，选B．‎ ‎6. 解析：由正弦定理得：，‎ 所以，即：，所以，选D．‎ ‎7. 解析：；；；；，此时输出，结合选项，选C.‎ ‎8. 解析：不超过的素数有，随机选取两个不同的数，其和等于的情况有和两种，所以概率为，选A．‎ ‎9. 解析：设的中点为，则平面，连结，则，‎ 由三垂线定理得，选D．‎ ‎10. 解析：因为，因为，由已知得：，所以， ‎ 由于，所以，解得，选B．‎ ‎11. 解析：，可推出为周期为2的函数，所以，选A.‎ ‎12. 解析：有题意可知，，所以，令,则，所以,所以，所以，选C.‎ 二、填空题 ‎13. 解析：因为，由导数的几何意义知，故曲线在点处的切线方程为.‎ ‎14. 解析：直线过定点，‎ 不等式组表示的区域如图：‎ 可知的取值范围是：.‎ ‎15. 解析：由得：，所以，‎ 由，所以，由得：，‎ ‎，所以， 所以．‎ ‎16. 解析：由题意可得，△△,所以,所以为三棱锥的外接球的直径，设，则，所以，所以三棱锥的外接球的半径，所以三棱锥的外接球体积的最小值为 三、解答题 ‎（一）必考题 ‎17. 解析：（1）时，‎ 时，由 …①‎ 可得 …②‎ ‎①-②，，‎ 因为适合，所以的通项公式为. ………6分 ‎（2）， …③‎ ‎，…④‎ ‎③-④得 ‎，. ………12分 ‎ ‎18. 解：（1）由已知，优等品的质量与尺寸的比在区间内，即，‎ 则随机抽取的6件合格产品中，有3件为优等品，3件为非优等品 ，‎ 现从抽取的6件合格产品中再任选3件，则取到优等品的件数，‎ ‎，，‎ ‎，． ‎ 的分布列为 所以． ………6分 ‎ ‎（2）解：对（）两边取自然对数得，‎ 令，得，且，根据所给统计量及最小二乘估计公式有，‎ ‎， ‎ ‎，得，故，‎ 所求关于的回归方程为． ………12分 ‎ ‎19.（1）证明：连接并延长交于，‎ 由已知得平面，且，‎ 所以，因为，‎ 所以平面，所以，‎ 因为四边形是平行四边形，且，‎ 所以四边形是菱形，‎ 所以，因为，所以平面，‎ 因为平面，所以平面平面 ‎. ………5分 ‎（2）解：连接，因为在底面上的射影是的重心，‎ 所以与全等，‎ 所以，因为，所以点为中点，所以，‎ 故平面与平面所成的二面角的平面角为，‎ 由，得，，，‎ 故可以为原点，，分别作为轴、轴、建立空间直角坐标系，则 ‎，，, , , ‎ 所以，，， ‎ 设为平面的一个法向量， 则，可取， ‎ 设平面的一个法向量为，则，可取，‎ 所以，‎ 即锐二面角的余弦值为. ………12分 ‎20. 解：(1)由条件可知，即点到的距离等于点到点的距离，‎ ‎ 所以点的轨迹是以为准线，为焦点的抛物线，‎ ‎ 其方程为：.………5分 ‎（2）设线段的垂直平分线与交于点，分别过点作，垂足为，‎ 再过点作，垂足为，‎ 因为， 所以∽，所以，‎ 设，(不妨设)，由抛物线定义得， ，‎ 所以，‎ 而，‎ 所以.………12分 ‎21. 解：（1）当时，，‎ 令，则，‎ 若，则，则，则在上单调递减，‎ 又，故，故在上单调递增，‎ 又，故对任意，恒成立；‎ 若，因为且，所以，则在上单调递减，又，‎ 故对任意，恒成立.‎ 综上，当时，对任意， 恒成立. ……… 5分 ‎ ‎（2）当时，在上单调递减，又，‎ 又则，，结合零点存在性定理知在内存在实数可使得，又，与在只有一个零点矛盾；‎ 当时，在上单调递减，又，‎ 结合零点存在性定理知在内存在实数可使得，故当时，‎ 即在上单调递增，又，故；‎ 构造函数，，则，则，‎ 故在单调递减，又，故，故在单调递减，‎ 又，故即，对任意恒成立，‎ 因为，所以，故，即，即，‎ 因为，且，‎ 即，由零点存在性定理知：在内存在实数可使，‎ 又，与在只有一个零点矛盾；‎ 综上，要使在只有一个零点，则. ……… 12分 ‎（二）选考题：第22、23题中任选一题做答。如果多做，则按所做的第一题记分。‎ ‎22. 解: （1） 将圆和圆的极坐标方程和两边乘， 由直角坐标和极坐标的互化公式：，，可得圆和圆的直角坐标方程分别为：：，两式相减可得圆和圆的公共弦所在直线的直角坐标方程为. ………5分 ‎（2）依题意可得两点的极坐标分别为,,所以 ‎,从而，当时等号成立，所以的最大值为. ………10分 ‎23. 证明: （1）依题意可得， ‎ 因为，‎ 所以， ………5分 ‎（2）要证:,只需证: ,只需证: ,两边平方后化简整理即是: ,由题设知， 成立，所以，不等式成立. ………10分