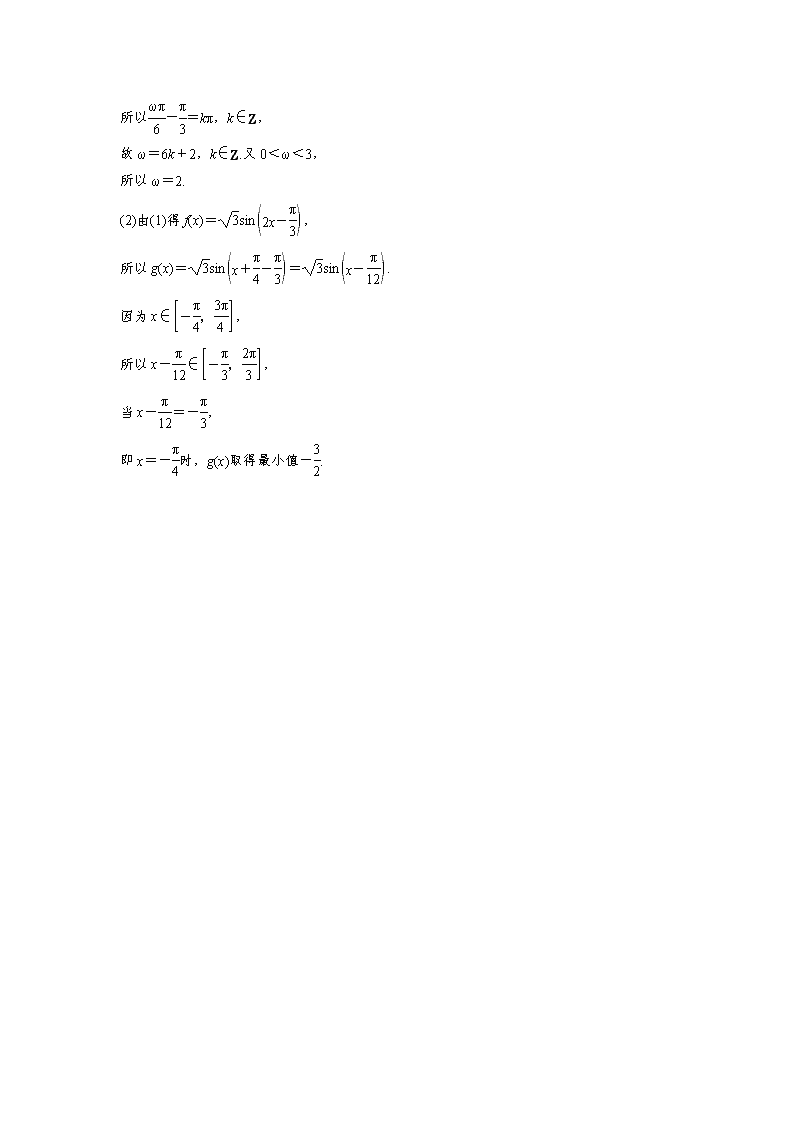2018届二轮复习（文）　三角函数的图象与性质学案（全国通用） 3页

规范答题示例4　三角函数的图象与性质 典例4　(12分)已知m＝(cos ωx，cos(ωx＋π))，n＝(sin ωx，cos ωx)，其中ω>0，f(x)＝m·n，且f(x)相邻两条对称轴之间的距离为.‎ ‎(1)若f＝－，α∈，求cos α的值；‎ ‎(2)将函数y＝f(x)的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，然后向左平移个单位长度，得到函数y＝g(x)的图象，求函数y＝g(x)的单调递增区间．‎ 审题路线图　(1) ‎(2) 规 范 解 答·分 步 得 分 构 建 答 题 模 板 解　f(x)＝m·n＝cos ωxsin ωx＋cos(ωx＋π)cos ωx ‎＝cos ωxsin ωx－cos ωxcos ωx＝－＝sin－. 3分 ‎∵f(x)相邻两条对称轴之间的距离为，‎ ‎∴T＝π，∴ω＝1，∴f(x)＝sin－. 4分 ‎(1)f＝sin－＝－，∴sin＝，‎ ‎∵α∈，sin＝>0，∴α－∈，∴cos＝. 6分 ‎∴cos α＝cos＝coscos －sinsin ‎＝×－×＝. 8分 ‎(2)f(x)经过变换可得g(x)＝sin－， 10分 令－＋2kπ≤x－≤＋2kπ，k∈Z，解得－＋2kπ≤x≤＋2kπ，k 第一步 化简：利用辅助角公式将f(x)化成y＝Asin(ωx＋φ)的形式．‎ 第二步 求值：根据三角函数的和差公式求三角函数值．‎ 第三步　‎ 整体代换：将“ωx＋φ”看作一个整体，确定f(x)的性质．‎ 第四步　‎ 反思：查看角的范围的影响，评价任意结果的合理性，检查步骤的规范性.‎ ‎∈Z，‎ ‎∴g(x)的单调递增区间是 (k∈Z).‎ ‎12分 评分细则　(1)化简f(x)的过程中，诱导公式和二倍角公式的使用各给1分；如果只有最后结果没有过程，则给1分；最后结果正确，但缺少上面的某一步过程，不扣分；‎ ‎(2)计算cos α时，算对cos给1分；由cos计算sin时没有考虑范围扣1分；‎ ‎(3)第(2)问直接写出x的不等式没有过程扣1分；最后结果不用区间表示不给分；区间表示式中不标出k∈Z不扣分；没有2kπ的不给分．‎ 跟踪演练3　(2017·山东)设函数f(x)＝sin＋sin，其中0＜ω＜3.已知f ＝0.‎ ‎(1)求ω；‎ ‎(2)将函数y＝f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变)，再将得到的图象向左平移个单位长度，得到函数y＝g(x)的图象，求g(x)在上的最小值．‎ 解　(1)因为f(x)＝sin＋sin，‎ 所以f(x)＝sin ωx－cos ωx－cos ωx ‎＝sin ωx－cos ωx ‎＝ ‎＝sin.‎ 由题设知f ＝0，‎ 所以－＝kπ，k∈Z，‎ 故ω＝6k＋2，k∈Z.又0＜ω＜3，‎ 所以ω＝2.‎ ‎(2)由(1)得f(x)＝sin，‎ 所以g(x)＝sin＝sin.‎ 因为x∈，‎ 所以x－∈，‎ 当x－＝－，‎ 即x＝－时，g(x)取得最小值－.‎