河北省衡水二中2020届高三下学期二模数学（理）试题 Word版含解析 28页

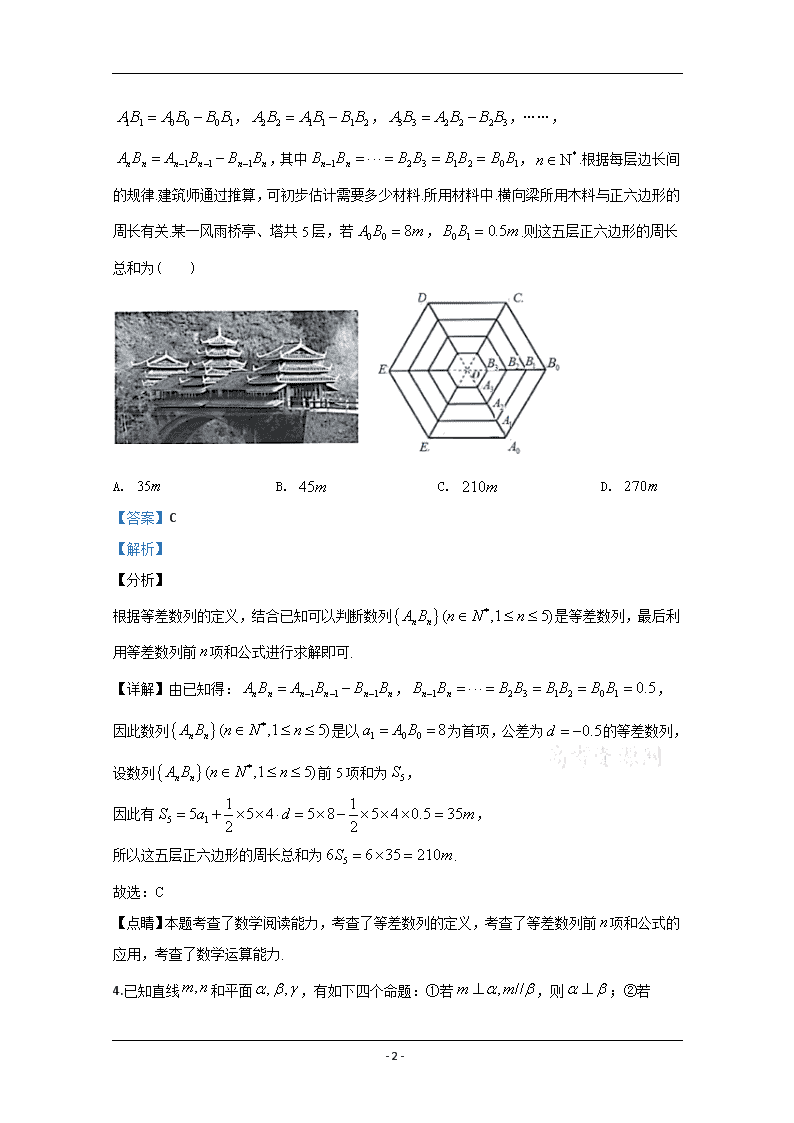
‎2019—2020学年度高二学期高三年级二模考试 数学（理科）试卷 第Ⅰ卷 一、选择题 ‎1.已知集合，，则（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 先确定集合中元素，然后根据交集定义求解．‎ ‎【详解】由题意，∴，‎ 故选：C．‎ ‎【点睛】本题考查集合的交集运算，属于简单题．‎ ‎2.设（为虚数单位），则（　　）‎ A. B. C. D. 2‎ ‎【答案】A ‎【解析】‎ 分析：直接利用复数代数形式乘除运算化简复数，然后求模即可．‎ 详解：∵复数 ‎ ．． 故选A. ‎ 点睛：本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．‎ ‎3.风雨桥是侗族最具特色建筑之一.风雨桥由桥、塔、亭组成.其亭、塔平面图通常是正方形、正六边形和正八边形.如图是风雨桥亭、塔正六边形的正射影.其正六边形的边长计算方法如下：‎ - 28 -‎ ‎，，，……，，其中，.根据每层边长间的规律.建筑师通过推算，可初步估计需要多少材料.所用材料中.横向梁所用木料与正六边形的周长有关.某一风雨桥亭、塔共5层，若，.则这五层正六边形的周长总和为( )‎ ‎ ‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据等差数列的定义，结合已知可以判断数列是等差数列，最后利用等差数列前项和公式进行求解即可.‎ ‎【详解】由已知得：，，‎ 因此数列是以为首项，公差为的等差数列，设数列前5项和为，‎ 因此有，‎ 所以这五层正六边形的周长总和为.‎ 故选：C ‎【点睛】本题考查了数学阅读能力，考查了等差数列的定义，考查了等差数列前项和公式的应用，考查了数学运算能力.‎ ‎4.已知直线和平面，有如下四个命题：①若，则；②若 - 28 -‎ ‎，则；③若，则；④若，则.其中真命题的个数是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据面面垂直，线面垂直以及线面平行的判定，即可容易判断.‎ ‎【详解】①若，则一定有，故①正确；‎ ‎②若，则，又因为，故可得，故②正确；‎ ‎③若，故可得//，又因为，故可得，故③正确；‎ ‎④若，则或，故④错误；‎ 综上所述，正确的有①②③.‎ 故选：C ‎【点睛】本题考查线面垂直，面面垂直的判定以及线面平行的判定，属综合基础题.‎ ‎5.下图可能是下列哪个函数图像（）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 可考虑用排除法，从函数的定义域和特殊点的函数的正负着手.‎ - 28 -‎ ‎【详解】由图像可知，在上单调递增，故可排除D；‎ 当时，A、选项中的选项中的 故选C.‎ ‎【点睛】本题考查函数的定义域和特殊点的函数值辨别图像，属于基础题.‎ ‎6.已知单位向量，，满足，则的值为（ ）‎ A. B. C. D. 1‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 先化简已知的等式，化简时把系数相同的放在同一侧，通过向量间的线性关系，得出各个点的位置，解三角形，最后可求数量积.‎ ‎【详解】∵，‎ ‎∴，‎ 如图，‎ 设中点为，则，且，‎ ‎∴三点共线，，，，‎ ‎∴为等腰三角形，‎ ‎∴，，‎ - 28 -‎ ‎∴，‎ ‎∴.‎ 故选：A.‎ ‎【点睛】本题考查向量的线性运算，通过线性运算的法则和性质判断出三角形形状，并解三角形，考查推理论证能力和运算求解能力，是中档题.‎ ‎7.疫情防控期间，衡水市某医院从3名呼吸科、3名重症科和3名急诊科医生中选派5人组成一个医疗专家小组跟本市其他医院的援助医疗队一同支援武汉，则该院呼吸科、重症科和急诊科医生都至少有1人的概率为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 先求出总的选法，三科医生都至少有1人的选派法可按所选医生个数分两类：311,221，由此可得选派方法数，从而计算出概率，‎ ‎【详解】从9人中选5人可种选法，三科医生都至少有1人，则按人数分为311,221，选派方法数为，∴所求概率为．‎ 故选：C．‎ ‎【点睛】本题考查古典概型，计算三科医生都至少有1人的选派方法数，按选派人数分类讨论是解题关键．‎ ‎8.条形码是由一组规则排列的条、空及其对应的代码组成，用来表示一定的信息，我们通常见的条形码是“”通用代码，它是由从左到右排列的个数字（用，，…，表示）组成，这些数字分别表示前缀部分、制造厂代码、商品代码和校验码，其中是校验码，用来校验前个数字代码的正确性．图（1）是计算第位校验码的程序框图，框图中符号表示不超过的最大整数（例如 - 28 -‎ ‎）．现有一条形码如图（2）所示（），其中第个数被污损，那么这个被污损数字是（ ）‎ ‎　　 ‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据程序框图可得到和分别表示前项中的偶数项之和与奇数项之和，从而得到，，进而得到；根据检验码可知；根据且可知，令可构造出方程求得；令可验证出不合题意，从而得到结果.‎ ‎【详解】由程序框图可知，表示的结果为前项中所有偶数项之和；表示的结果为前项中所有奇数项之和，‎ 则：，‎ - 28 -‎ ‎，，即：‎ 且 ‎ 当时，，此时：，解得：‎ 当时，，此时： ‎ 综上所述：‎ 本题正确选项：‎ ‎【点睛】本题考查根据程序框图的功能补全数据的问题，关键是能够读懂程序框图中每一步的功能，从而准确构造出方程求得结果.‎ ‎9.下图统计了截止到2019年年底中国电动汽车充电桩细分产品占比及保有量情况，关于这5次统计，下列说法正确的是（ ）‎ ‎①私人类电动汽车充电桩保有量增长率最高的年份是2018年 - 28 -‎ ‎②公共类电动汽车充电桩保有量的中位数是25．7万台 ‎③公共类电动汽车充电桩保有量的平均数为23．12万台 ‎④从2017年开始，我国私人类电动汽车充电桩占比均超过50%‎ A. ②④ B. ①②③ C. ①④ D. ④‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据保有量情况图表计算增长率，平均数，确定中位数可判断①②③，从占比情况图表知 易判断④．‎ ‎【详解】从保有量情况图表知 私人类电动汽车充电桩保有量增长率最高的年份是2016年，①错；‎ 公共类电动汽车充电桩保有量的中位数是21.4万台，②错；‎ 公共类电动汽车充电桩保有量的平均数为万台，③错；‎ 从占比情况图表知，从2017年开始，我国私人类电动汽车充电桩占比均超过50%，④正确．‎ 故选：D．‎ ‎【点睛】本题考查统计图表，正确认识统计图表是解题关键．属于基础题．‎ ‎10.已知抛物线的方程为，为其焦点，过的直线与抛物线交于两点（点在轴上方），点，连接交轴于，过作交于，若，则斜率为( )‎ A. B. C. D. 2‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据抛物线方程，求得焦点坐标和准线方程，作垂直于准线交准线于，画出几何关系图形.由且，可得，结合抛物线定义可知 - 28 -‎ 求得点的横坐标，代入抛物线方程可求得纵坐标.由两点间斜率公式可得直线斜率，即为的斜率.‎ ‎【详解】抛物线的方程为，为其焦点，过的直线与抛物线交于两点（点在轴上方），点，连接交轴于，‎ 则，准线方程为.‎ 根据题意画出几何关系如下图所示：作垂直于准线交准线于.‎ 且，‎ 则，‎ 垂直于准线交准线于，则，‎ 即，解得，‎ 代入抛物线方程可得，‎ 斜率，即为的斜率，所以.‎ 故选：A.‎ - 28 -‎ ‎【点睛】本题考查了抛物线标准方程及其几何性质的综合应用，平行线分线段成比例性质应用，直线与抛物线位置关系的综合应用，属于中档题.‎ ‎11.一副三角板由一块有一个内角为的直角三角形和一块等腰直角三角形组成，如图所示，，，，．现将两块三角板拼接在一起，取中点与中点，则下列直线与平面所成的角不为定值的是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 通过证明平面，可以找到与平面所成的角，计算可知都为定值，由此可得答案.‎ ‎【详解】因为为中点，所以，所以，‎ 又，且，‎ 所以平面，‎ 所以与平面所成的角分别为和，它们相等，等于45°，‎ 根据直线与平面所成角的定义知，与平面 所成的角为 故只有与平面所成的角不为定值.‎ 故选：B ‎【点睛】本题考查了直线与平面垂直的判定定理，考查了直线与平面所成角，属于基础题.‎ ‎12.若函数在上存在两个极值点，则的取值范围是（ ）‎ A. B. ‎ C. D. ‎ - 28 -‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由导函数的连续性，问题转化为在上有两个不等实根，其中一根为，由在上有不为1的另一根，采取分离参数法可得参数范围．‎ ‎【详解】由题意可知有两个不等根．方程 ‎，，有一根．中，另一根满足方程（）， ‎ 令，，，‎ 所以在上单调递增．所以，‎ 即．所以．‎ 故选：C．‎ ‎【点睛】本题考查由函数极值点个数求参数范围，问题首先转化为方程在有两个不等式实根，再转化为方程（）有一个实根，从而转化为求函数的值域，考查了等价转化思想．‎ 第Ⅱ卷 二、填空题 ‎13.已知双曲线C：的离心率为2，焦点到渐近线的距离为，则双曲线C的焦距为_____________．‎ ‎【答案】4.‎ ‎【解析】‎ ‎【分析】‎ 利用双曲线的性质及条件列a,b,c的方程组，求出c可得.‎ ‎【详解】因为双曲线的离心率为2，焦点到渐近线的距离为 ，所以 - 28 -‎ ‎,解得，所以双曲线的焦距为4.故答案为4.‎ ‎【点睛】本题考查双曲线的几何性质，注意隐含条件，考查运算求解能力，属于基础题.‎ ‎14.设数列的前项和为，且满足，则____．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由题意可得数列的首项为，在中将换为，两方程相减可得数列的通项公式，再由等比数列求和公式计算可得所求和．‎ ‎【详解】解：，‎ 可得时， ，‎ 时，，‎ 又，‎ 两式相减可得，‎ 即，‎ 上式对也成立，‎ 可得数列是首项为1，公比为的等比数列，‎ 可得．‎ 故答案为．‎ ‎【点睛】本题主要考查了赋值法及等比数列的前 - 28 -‎ 项和公式，考查计算能力及分析能力，属于中档题．‎ ‎15.如图，在等边三角形ABC中， AB=6.动点P从点A出发，沿着此三角形三边逆时针运动回到A点，记P运动的路程为x，点P到此三角形中心O距离的平方为f(x)，给出下列三个结论：‎ ‎①函数f(x)的最大值为12；‎ ‎②函数f(x)的图象的对称轴方程为x=9；‎ ‎③关于x的方程最多有5个实数根.‎ 其中，所有正确结论的序号是____.‎ ‎【答案】①②‎ ‎【解析】‎ ‎【分析】‎ 写出分别在上运动时的函数解析式，利用分段函数图象可解.‎ ‎【详解】‎ 分别在上运动时的函数解析式，‎ 分别在上运动时的函数解析式，‎ 分别在上运动时的函数解析式，‎ ‎，‎ 由图象知：正确的是①②.‎ 故答案为：①②‎ - 28 -‎ ‎【点睛】利用函数图象可以解决很多与函数有关的问题，如利用函数的图象解决函数性质问题，函数的零点、方程根的问题，有关不等式的问题等.解决上述问题的关键是根据题意画出相应函数的图象，利用数形结合思想求解.‎ ‎16.在三棱锥中，，二面角的余弦值为，当三棱锥的体积的最大值为时，其外接球的表面积为______．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 设球心在平面内的射影为，在平面内的射影为，取中点，‎ 则二面角的平面角为，点在截面圆上运动，点在截面圆上运动，由图知，当，时，三棱锥的体积最大，此时与是等边三角形，由此计算出，求得球半径，得面积．‎ ‎【详解】如图所示，设球心在平面内的射影为，在平面内的射影为 则二面角的平面角为（其中是中点），点在截面圆上运动，点在截面圆上运动，由图知，当，时，面积最大，到平面距离最大，三棱锥的体积最大，此时与是等边三角形，共线，线，‎ 设，则，．‎ ‎，则，，‎ 解得，所以，，，‎ ‎，则，，∴，，‎ - 28 -‎ ‎∴，球的半径，‎ 所求外接球的表面积为．‎ 故答案为：．‎ ‎【点睛】本题考查求球的表面积，解题时作出图形，通过点的运动得出三棱锥体积最大时，点位置，从而通过体积计算出棱长，半径，表面积．考查了学生的空间想象能力，运算求解能力．属于中档题．‎ 三、解答题 ‎17.如图，在中，，且 ‎（）求的值；‎ 若，且，求及.‎ ‎【答案】（Ⅰ）（Ⅱ）,‎ ‎【解析】‎ ‎【分析】‎ - 28 -‎ ‎（Ⅰ）利用可得的值.‎ ‎（Ⅱ）在和中利用余弦定理构建关于的方程组，结合（Ⅰ）中结果可求的值，求出后可计算从而得到.‎ ‎【详解】（Ⅰ）在中，，‎ ‎ ，其中为边上的高.‎ 又 ，‎ ‎ ‎ ‎（Ⅱ）在中，‎ ‎ ……①‎ 在中，‎ ‎ ……②‎ 而，即，‎ 所以，，解得，‎ ‎ ， . ‎ 又因为，‎ ‎ ，‎ ‎ ， .‎ ‎【点睛】‎ - 28 -‎ 三角形中共有七个几何量（三边三角以及外接圆的半径），一般地，知道其中的三个量（除三个角外），可以求得其余的四个量.‎ ‎（1）如果知道三边或两边及其夹角，用余弦定理；‎ ‎（2）如果知道两边即一边所对的角，用正弦定理（也可以用余弦定理求第三条边）；‎ ‎（3）如果知道两角及一边，用正弦定理.‎ 另外，注意在解三角形中，我们有时需要找出不同三角形之间相关联的边或角，由它们沟通分散在不同三角形的几何量．‎ ‎18.如图，四棱锥的底面是平行四边形，连接，其中，.‎ ‎（1）求证：；‎ ‎（2）若，，，求二面角的正弦值.‎ ‎【答案】(1)见解析；(2) ‎ ‎【解析】‎ 试题分析：.（1）取中点，易证面，所以，（2）以所在直线分别为轴建立空间直角坐标系，平面的法向量，设平面的法向量=，，即.‎ 试题解析：‎ ‎（1）证明：取中点，连，‎ ‎∵，‎ ‎∴，，∵‎ ‎∴面，又∵面，∴‎ - 28 -‎ ‎（2）∵，，，‎ ‎∴是等腰三角形，是等边三角形，∵，∴，.‎ ‎∴，∴‎ 以所在直线分别为轴建立空间直角坐标系，‎ 则，，，‎ 从而得，，，‎ 设平面的法向量 则，即，∴，‎ 设平面的法向量，‎ 由，得，∴‎ ‎∴‎ 设二面角为，∴‎ 点睛：利用法向量求解空间二面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.‎ - 28 -‎ ‎19.已知，为椭圆的左右焦点，过的直线交椭圆于，两点，的周长为8.‎ ‎（1）求椭圆的标准方程；‎ ‎（2）已知是直线上一动点，若，与轴分别交于点，，则是否为定值，若是，求出该定值，若不是，请说明理由.‎ ‎【答案】（1）（2）是定值；定值为 ‎【解析】‎ ‎【分析】‎ ‎（1）由条件得出，即可 ‎（2）设直线的方程为，，，，联立直线与椭圆的方程消元，然后韦达定理可得，，然后算出，，然后算出即可 ‎【详解】（1）依题意，‎ 由椭圆的定义可得的周长为，即，所以，‎ 故椭圆的方程为.‎ ‎（2）设直线的方程为，，，，‎ 由得，‎ 显然，则，，‎ - 28 -‎ 直线，令得，‎ 即，同理，‎ ‎，‎ 同理：，‎ 于是：‎ 所以为定值.‎ ‎【点睛】涉及椭圆的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”“整体带入”等解法.‎ ‎20.已知函数.‎ ‎（1）证明：；‎ ‎（2）（i）证明：当时，对任意，总有；‎ ‎（ii）讨论函数的零点个数.‎ ‎【答案】（1）证明见解析（2）（i）证明见解析（ii）当或时，函数有唯一零点；当且时，函数有两个零点 ‎【解析】‎ ‎【分析】‎ ‎（1），用导数法求得最小值大于零即可。‎ - 28 -‎ ‎（2）（i）证明：由（1）知：，根据，利用根的分布证明。（ii）将的零点问题，转化为的零点问题，求导，分，, ，，四种情况讨论求解。‎ ‎【详解】（1）令，‎ 则.‎ 当时，；当时，，‎ 故在上单调递减；在上单调递增，‎ 所以，即.‎ ‎（2）（i）证明：由（1）知：‎ ‎.‎ 当，时，，‎ ‎，故.‎ ‎（ii），令，则.‎ 因为函数的定义域为，‎ 故的零点与的零点相同，‎ 所以下面研究函数在上零点个数.‎ ‎∵，∴.‎ - 28 -‎ ‎①当时，在上恒成立，‎ ‎∴在上单调递增.‎ ‎∵，.‎ ‎∴存在唯一的零点，使得.‎ ‎②当时，，‎ 可得在上单调递减，在上单调递增.‎ ‎∴的最小值为.‎ 令，则，‎ 所以在上单调递增，在上单调递减，又.‎ 当时，有唯一零点；‎ 当，即时，且.‎ ‎∵，∴在上有唯一的零点.‎ 又由（i）知：在上存在唯一零点，不妨设，‎ ‎∴在上有唯一的零点，‎ 故此时在上有两个零点；‎ 当，即时，且，，.‎ 又，由函数零点存在定理可得在上有唯一零点，‎ 故在，上各一个唯一零点.‎ 综上可得：当或时，函数有唯一零点；‎ 当且时，函数有两个零点.‎ ‎【点睛】‎ - 28 -‎ 本题主要考查导数证明不等式，导数与函数的零点，还考查了转化化归，分类讨论的思想和运算求解的能力，属于难题.‎ ‎21.2020年是具有里程碑意义的一年我们将全面建成小康社会，实现第一个百年奋斗目标；2020年也是脱贫攻坚决战决胜之年．（总书记二O二O年新年贺词）截至2018年底，中国农村贫困人口从2012年的9899万人减少至1660万人，贫困发生率由2012年的下降至2018年的；连续7年每年减贫规模都在1000万人以上；确保到2020年农村贫困人口实现脱贫，是我们党立下的军令状，脱贫攻坚越到最后时刻，越要响鼓重锤．某贫困地区截至2018年底，按照农村家庭人均年纯收入8000元的小康标准，该地区仅剩部分家庭尚未实现小康．现从这些尚未实现小康的家庭中随机抽取50户，得到这50户家庭2018年的家庭人均年纯收入的频率分布直方图．‎ ‎（1）将家庭人均纯年收入不足5000元的家庭称为"特困户”若从这50户家族中再取出10户调查致贫原因，求这10户中含有"特困户"的户数X的数学期望；‎ ‎（2）2019年7月，为估计该地能否在2020年全面实现小康，统计了该地当时最贫困的一个家庭2019年1至6月的人均月纯收入如下表：‎ 月份/2019（时间代码）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 人均月纯收入（元）‎ ‎275‎ ‎365‎ ‎415‎ ‎450‎ ‎470‎ ‎485‎ 由散点图及相关性分析发现:家庭人均月纯收入与时间代码之间具有较强的线性相关关系，由此估计该家庭2020年能实现小康生活，但2020年1月突如其来的新冠肺炎疫情影响了奔小康的进展，该家庭2020年第一季度（1，2，3月份）每月的人均月纯收入人均只有2019‎ - 28 -‎ 年12月的预估值的，为加快脱贫进程，政府加大扶贫力度，拟从2020年3月份起，以后每月的增长率为，为了使2020年该家庭顺利迈入小康生活，则至少应为多少?（保留小数点后两位数字）；‎ ‎①可能用到的数据:‎ ‎②参考公式:线性回归方程中，‎ ‎【答案】（1）（户）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由频率分布直方图求出这50户家族中特困户的户数，服从超几何分布，利用超几何分布数学期望的计算方法即可得解；‎ ‎（2）分别计算的平均数，根据公式求得，得到回归方程，借助回归方程即可得到2020年第一季度该家庭人均月纯收入，求出从开始3月份到12月份的月纯收入之和，建立不等式，得到，通过求解不等式即可求出的最小值，从而得解.‎ ‎【详解】（1）由频率分布直方图可知，‎ 家庭人均年收入在元的家庭数为:户；‎ 家庭人均年收入在元的家庭数为:户；‎ 家庭人均年收入在元的家庭数为:户；‎ 家庭人均年收入在元的家庭数为:户；‎ 家庭人均年收入在元的家庭数为:户；‎ 家庭人均年收入在元的家庭数为:户；‎ - 28 -‎ 共计50户，其中家庭人均年收入不足5000元的特困户有：户，‎ 由题意：满足参数为50，23，10的超几何分布，所以户；‎ 即这10户中含有“特困户”的户数的数学期望为（户）.‎ ‎（2）由题意得：，‎ ‎，‎ ‎，‎ 所以：，‎ ‎，‎ 所以回归直线方程为：，‎ 令，则可知2019年12月份该家庭人均月纯收入为（元），‎ 所以，2020年第一季度该家庭人均月纯收入为（元），‎ 设从开始3月份到12月份的月纯收入之和为，‎ 则 由题意应有：，‎ 即：，‎ 显然是以为自变量的增函数， ‎ ‎①当时，显然成立，‎ - 28 -‎ ‎②当时，，‎ ‎（舍）‎ 或，‎ 所以，为了使2020年该家庭顺利迈入小康生活，则至少应为；‎ ‎【点睛】本题考查了频率分布直方图，求解回归方程，利用回归方程求解预估值的问题，其中涉及到等比数列的求和公式以及解不等式等知识点，考查了学生的数据处理能力，对于学生的运算求解能力有一定的要求，难度较大.‎ 请考生在第（22）、（23）题中任选一题做答，如果多做，则按所做的第一题计分，做答时请写清题号．‎ 选修4-4：坐标系与参数方程 ‎22.如图，有一种赛车跑道类似“梨形”曲线，由圆弧和线段AB，CD四部分组成，在极坐标系Ox中，A（2，），B（1，），C（1，），D（2，），弧所在圆的圆心分别是（0，0），（2，0），曲线M1是弧，曲线M2是弧．‎ ‎（1）分别写出M1，M2的极坐标方程：‎ ‎（2）点E，F位于曲线M2上，且，求△EOF面积的取值范围．‎ ‎【答案】（1）M1，M2的极坐标方程为和ρ＝4cosθ（）．（2）．‎ ‎【解析】‎ - 28 -‎ ‎【分析】‎ ‎（1）利用圆的极坐标方程的求法求解．‎ ‎（2）设点E（ρ1，α），点F（），（），得到ρ1＝4cosα，，然后代入，利用三角恒等变换化简求解.‎ ‎【详解】（1）由题意可知：M1的极坐标方程为．‎ 记圆弧AD所在圆的圆心（2，0），‎ 因为，‎ 所以极点O在圆弧AD上．‎ 设P（ρ，θ）为M2上任意一点，则ρ＝4cosθ（）．‎ 所以：M1，M2的极坐标方程为和ρ＝4cosθ（）．‎ ‎（2）设点E（ρ1，α），点F（），（），‎ 所以ρ1＝4cosα，．‎ 所以．‎ 由于，所以．‎ 故．‎ ‎【点睛】本题主要考查极坐标方程的求法，三角形面积公式以及三角恒等变换与三角函数的性质的应用，还考查了运算能力和转换能力，属于中档题．‎ 选修4-5：不等式选讲 ‎23.已知f（x）＝|x2+2﹣t|+|t﹣3|（x＞0）．‎ - 28 -‎ ‎（1）若f（1）＝2，求实数t的取值范围；‎ ‎（2）求证：f（x）≥2．‎ ‎【答案】（1）[1，3]；（2）见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）利用绝对值三角不等式的性质可得（3﹣t）（t﹣1）≥0，解出即可；‎ ‎（2）利用绝对值三角不等式及基本不等式即可得证．‎ ‎【详解】（1）∵f（1）＝|3﹣t|+|t﹣1|≥|3﹣t+t﹣1|＝2，取等号的条件为（3﹣t）（t﹣1）≥0，‎ 解得1≤t≤3，即实数t的取值范围为[1，3]；‎ ‎（2）证明：易知，‎ ‎∵x＞0，‎ ‎∴，当且仅当，即时，取等号.‎ ‎∴，‎ ‎∴f（x）≥2．‎ ‎【点睛】本题主要考查绝对值三角不等式，均值不等式和二次不等式的应用，还考查了运算求解的能力，属于中档题.‎ - 28 -‎