高中数学选修2-2教学课件4_3_2《函数的极值与导数》（1） 27页

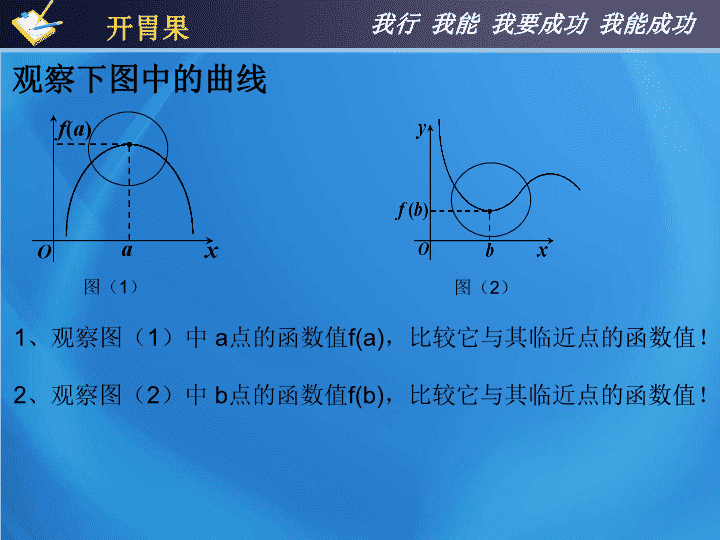
绘画使人赏心悦目， 诗歌能动人心弦， 哲学使人获得智慧 ， 科学可改善物质生活， 但数学能给予以上的一切。 数学是人类最高超的成就， 也是人类心灵最独特的创作。 音乐能激发或抚慰情怀， 行动指南： 策略＋方法＋勤奋＋信心＋恒心＝成功 我行 我能 我要成功 我能成功 1 、观察图（ 1 ）中 a 点的函数值 f(a) ，比较它与其临近点的函数值！ 观察下图中的曲线 图（ 1 ） 图（ 2 ） 2 、观察图（ 2 ）中 b 点的函数值 f(b) ，比较它与其临近点的函数值！ 开胃果 我行 我能 我要成功 我能成功 开胃果 我行 我能 我要成功 我能成功 思考 ： 函数 y ＝ f ( x ) 在点 x ＝ 0 ， x ＝ 2 处的 函数值，与它们附近所有各点处 的函数值，比较有什么特点 ? 。 2 、观察函数 的图象， f(0) f(2) 这时的函数值叫做函数的极值 探究 （ 3 ）在点 附近 , 的导数的符号有什么规律 ? （ 1 ）函数 在点 的函数值与这些点附近的 函数值有什么关系 ? （ 2 ）函数 在点 的导数值是多少 ? ( 图一 ) 问题： 探究 ( 图一 ) ( 图二 ) 极大值 f(b) 点 a 叫做函数 y=f(x) 的 极小值点 ， f( a ) 叫做函数 y=f(x) 的 极小值 . 点 b 叫做函数 y=f(x) 的 极大值点 ， f( b ) 叫做函数 y=f(x) 的 极大值 . 极小值点 、 极大值点 统称 极值点 ， 极大值 和 极小值 统称为 极值 . 极小值 f(a) 思考： 极大值一定大于极小值吗？ 我行 我能 我要成功 我能成功 一般地，设函数 f ( x ) 在 点 a 、 b 附近有定义 ， 如果对 a 附近的所有的点 , 都有 f ( x )﹤ f ( a ) , 我们 就说 f ( a ) 是函数 f ( x ) 的一个 极大值 , 记作 : y 极大值 = f ( a ) ； 函数极值的定义 数学建构 如果对 b 附近的所有的点 , 都有 f ( x )﹥ f ( b ) ， 我们就说 f ( b ) 是函数 f ( x ) 的一个 极小值 ， 记作 : y 极小值 = f ( b ) . 点 a 叫做函数 y=f(x) 的 极大值点 . 极大值与极小值统称为 极值 . 点 b 叫做函数 y=f(x) 的 极小值点 . 1 、极值是局部性质还是整体而言？ 2 、极值唯一吗？ 3 、极大值与极小值大小关系是否确定？ o a x 1 x 2 x 3 x 4 b x y P ( x 1 , f ( x 1 )) y=f ( x ) Q ( x 2 , f ( x 2 )) 我行 我能 我要成功 我能成功 回味反思 观察下列图像，结合定义思考以下问题： （ 1 ） 极值是某一点附近的小区间而言 的 , 是函数的局部性质 , 不是整体的最值 ; （ 2 ） 函数的极值不一定唯一 , 在整个定义区间内可能有多个极大值和极小值； （ 3 ） 极大值与极小值没有必然关系，极大值可能比极小值还小 . 观察图像并类比于函数的单调性与导数关系的研究方法 , 看极值与导数之间有什么关系 ? o a x 0 b x y x x 0 左侧 x 0 x 0 右侧 f  ( x ) f ( x ) o a x 0 b x y x x 0 左侧 x 0 x 0 右侧 f  ( x ) f ( x ) 增 f  ( x ) >0 f  ( x ) =0 f  ( x ) <0 极大值 减 f  ( x ) <0 f  ( x ) =0 增 减 极小值 f  ( x ) >0 请问如何判断 f ( x 0 ) 是极大值或是极小值？ 导数 左正右负为极大，右正左负为极小 我行 我能 我要成功 我能成功 数学建构 函数 左增右减为极大，右增左减为极小 （ 1 ）如图是函数 的图象 , 试找出函数 的 极值点 , 并指出哪些是极大值点 , 哪些是极小值点？ （ 2 ）如果把函数图象改为导函数 的图象 ? 随堂练习 答： 1 、 x 1 ,x 3 ,x 5 ,x 6 是函数 y=f(x) 的极值点，其中 x 1 ,x 5 是函 数 y=f(x) 的极大值点， x 3 ,x 6 函数 y=f(x) 的极小值点。 2 、 x 2 ,x 4 是函数 y=f(x) 的极值点 , 其中 x 2 是函数 y=f(x) 的极大值点， x 4 是函数 y=f(x) 的极小值点。 函数 y = f ( x ) 的导数 y ' 与函数值和极值之间的关系为 ( ) A 、导数 y ' 由负变正 , 则函数 y 由减变为增 , 且有极大值 B 、导数 y ' 由负变正 , 则函数 y 由增变为减 , 且有极大值 C 、导数 y ' 由正变负 , 则函数 y 由增变为减 , 且有极小值 D 、导数 y ' 由正变负 , 则函数 y 由增变为减 , 且有极大值 D 我行 我能 我要成功 我能成功 学生活动 练习 1 (-∞,-2) 当 x 变化时 , f  ( x) 、 f ( x ) 的变化情况如下表： 我行 我能 我要成功 我能成功 小试牛刀篇 f ( x ) f  ( x ) x ∴ 当 x =-2 时 , y 极大值 =17/3 ； 当 x = 2 时 , y 极小值 =-5 . -2 (-2,2) 2 (2,+∞) + 0 0 - + 极大值 f(-2) 极小值 f(2) 解 : ∵ 又 ∵ f  ( x ) = x 2 - 4 , 由 f  ( x ) =0 解得 x 1 =2, x 2 =-2. 练习 2 求下列函数的极值 : 解 : 令 解得 列表 : x 0 f ( x ) + 单调递增 单调递减 – 所以 , 当 时 , f ( x ) 有极小值 练习 2 求下列函数的极值 : 解 : 解得 列表 : x (– ∞ , –3) –3 (–3 , 3) 3 ( 3 , + ∞ ) 0 0 f ( x ) – + + 单调递增 单调递减 单调递增 所以 , 当 x = – 3 时 , f ( x ) 有极大值 54 ; 当 x = 3 时 , f ( x ) 有极小值 – 54 . 练习 2 求下列函数的极值 : 解 : 解得 所以 , 当 x = – 2 时 , f ( x ) 有极小值 – 10 ; 当 x = 2 时 , f ( x ) 有极大值 22 . 解得 所以 , 当 x = – 1 时 , f ( x ) 有极小值 – 2 ; 当 x = 1 时 , f ( x ) 有极大值 2 . 练习 3 下图是导函数 的图象 , 在标记的点中 , 在 哪一点处 (1) 导函数 有极大值 ? (2) 导函数 有极小值 ? (3) 函数 有极大值 ? (4) 函数 有极小值 ? 或 我行 我能 我要成功 我能成功 渐入佳境篇 探索 : x =0 是否为函数 f ( x )= x 3 的极值点 ? x y O f ( x )  x 3 若寻找可导函数极值点 , 可否只由 f  ( x ) = 0 求得即可 ? f  ( x ) =3 x 2 当 f  ( x ) =0 时， x =0 ，而 x =0 不是 该函数的极值点 . f  ( x 0 ) =0 x 0 是可导函数 f ( x ) 的极值点 x 0 左右侧导数异号 f  ( x 0 ) =0 x 0 是函数 f(x) 的极值点 我行 我能 我要成功 我能成功 请思考求可导函数的极值的步骤 : 3, 检查 在方程 ＝ 0 的根的左右两侧的 符号，确定极值点。 ( 通过列表法 ) 1. 确定函数的定义域，求导数 2. 求方程 =0 的根 , 这些根也称为 可能 极值点； 一览众山小 要想知道 x 0 是极大值点还是极小值点就必须判断 f  ( x 0 ) =0 左右侧导数的符号 . 强调 我行 我能 我要成功 我能成功 感受高考 （ 2006 年天津卷 ) 函数 的定义域为开区间 导函数 在 内的图像如图所示，则函数 在开区间 内有（ ）个极小值点。 A .1 B .2 C .3 D. 4 A 注意： 数形结合以及原函数与导函数图像的区别 x 1 x 2 x 3 我行 我能 我要成功 我能成功 案例分析 函数 在 时有极值 10 ，则 a ， b 的值为（ ） A 、 或 B 、 C 、 D 、 以上都不对 C 解 : 由题设条件得： 解之得 注意： f / ( x 0 )=0 是函数取得极值的必要不充分条件 注意代入检验 通过验证，只有 合要求，故应选择 C 。 我行 我能 我要成功 我能成功 变式训练 函数 f ( x ) =x 3 +3 ax 2 +3( a +2) x +3 既有极大值，又有极小值，则 a 的取值范围为 。 注意： 导数与方程、不等式的结合应用 我行 我能 我要成功 我能成功 一吐为快篇 本节课主要学习了哪些内容？ 请想一想？ 1 、极值的判定方法 2 、极值的求法 注意点： 1 、 f ′ ( x 0 )= 0 是函数取得极值的必要不充分条件 2 、数形结合以及函数与方程思想的应用 3 、 要想知道 x 0 是极大值点还是极小值点就必须判断 f  ( x 0 ) =0 左右侧导数的符号 . 绘画使人赏心悦目， 诗歌能动人心弦， 哲学使人获得智慧 ， 科学可改善物质生活， 但数学能给予以上的一切。 数学是人类最高超的成就， 也是人类心灵最独特的创作。 音乐能激发或抚慰情怀， 行动指南： 策略＋方法＋勤奋＋信心＋恒心＝成功 我行 我能 我要成功 我能成功 （ 2007 全国 ） 设函数 感受高考 注意： 函数与方程思想的应用 在 及 时取得极值 , 求 a 、 b 的值。 a=-3,b=4 高考经典 2 　 (2011 年高考重庆卷 ) 设 f ( x ) ＝ x 3 ＋ ax 2 ＋ bx ＋ 1 的导数 f ′ ( x ) 满足 f ′ (1) ＝ 2 a ， f ′ (2) ＝－ b ，其中常数 a ， b ∈ R. (1) 求曲线 y ＝ f ( x ) 在点 (1 ， f (1)) 处的切线方程； (2) 设 g ( x ) ＝ f ′ ( x )e － x ，求函数 g ( x ) 的极值． 解： (1) 因为 f ( x ) ＝ x 3 ＋ ax 2 ＋ bx ＋ 1 ，故 f ′ ( x ) ＝ 3 x 2 ＋ 2 ax ＋ b . 令 x ＝ 1 ，得 f ′ (1) ＝ 3 ＋ 2 a ＋ b ，由已知 f ′ (1) ＝ 2 a ， 因此 3 ＋ 2 a ＋ b ＝ 2 a ，解得 b ＝－ 3. 又令 x ＝ 2 ，得 f ′ (2) ＝ 12 ＋ 4 a ＋ b ，由已知 f ′ (2) ＝－ b ， (2) 由 (1) 知 g ( x ) ＝ (3 x 2 － 3 x － 3)e － x ， 从而有 g ′ ( x ) ＝ ( － 3 x 2 ＋ 9 x )e － x . 令 g ′ ( x ) ＝ 0 ，得－ 3 x 2 ＋ 9 x ＝ 0 ，解得 x 1 ＝ 0 ， x 2 ＝ 3. 当 x ∈ ( － ∞ ， 0) 时， g ′ ( x )<0 ，故 g ( x ) 在 ( － ∞ ， 0) 上为减函数； 当 x ∈ (0,3) 时， g ′ ( x )>0 ，故 g ( x ) 在 (0,3) 上为增函数； 当 x ∈ (3 ，＋ ∞ ) 时， g ′ ( x )<0 ，故 g ( x ) 在 (3 ，＋ ∞ ) 上为减函数． 从而函数 g ( x ) 在 x 1 ＝ 0 处取得极小值 g (0) ＝－ 3 ，在 x 2 ＝ 3 处取得极大值 g (3) ＝ 15e － 3 .