河北省邯郸市大名一中2020届高三上学期第十周周测数学（文）试卷 7页

数学（文科）周测试题 一．本大题共12小题，每小题5分，共60分 ‎1.已知集合，，则 A. B. C. D. ‎ ‎2.设为虚数单位，，若是纯虚数，则 A.2 B. C. 1 D. ‎ ‎3.‎ A. B. C. D. ‎ ‎4.下列说法中正确的是 A. 先把高三年级的2000名学生编号：1到2000，再从编号为1到50的50名学生中随机抽取1名学生，其编号为，然后抽取编号为的学生，这样的抽样方法是分层抽样法 B. 线性回归直线不一定过样本中心点 ‎ C. 若两个随机变量的线性相关性越强，则相关系数的值越接近于1‎ D.若一组数据1、、3的平均数是2，则该组数据的方差是 ‎5.执行如图所示的程序框图，若输入的为2，则输出的值是 A. 2 B. 1 C. D.‎ ‎6.已知数列满足，，则 A.8 B. 16 C. 32 D. 64‎ ‎7.已知实数满足，则的最小值是 A. 5 B. C. D. ‎ ‎8. 从集合中随机抽取两数，则满足的概率是 A. B. C. 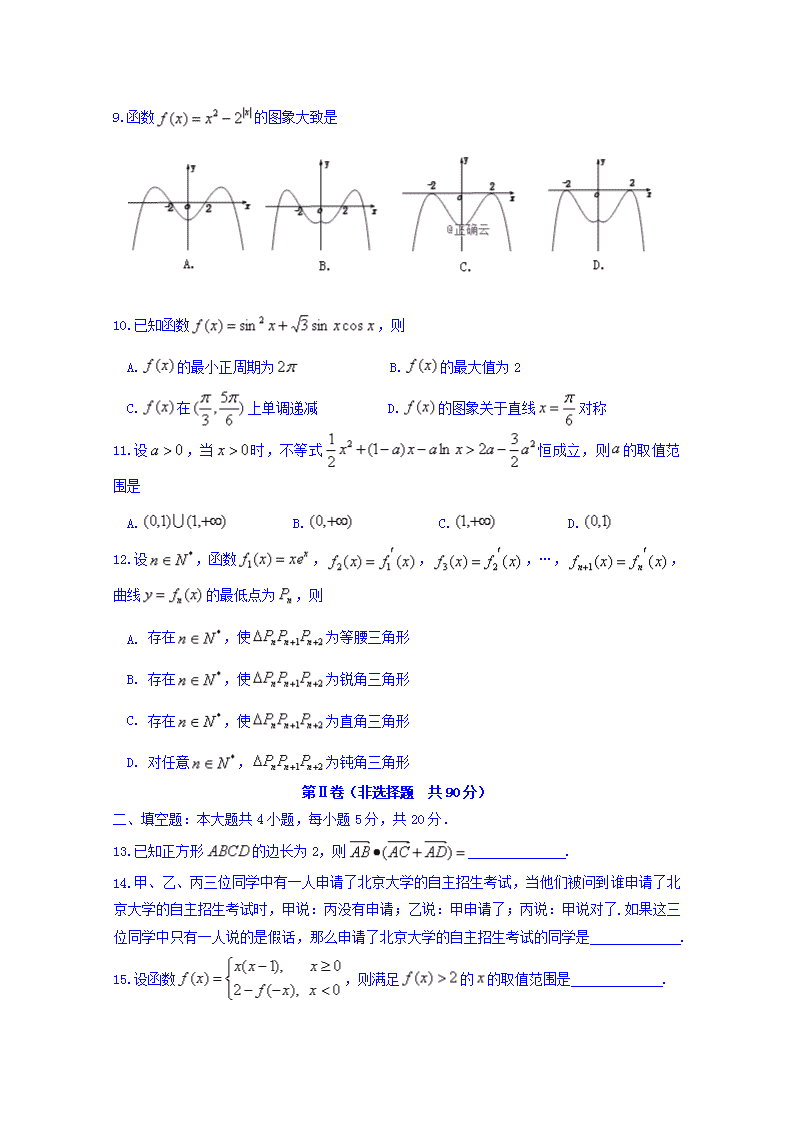D.‎ ‎9.函数的图象大致是 ‎10.已知函数，则 A.的最小正周期为 B.的最大值为2 ‎ C.在上单调递减 D.的图象关于直线对称 ‎11.设，当时，不等式恒成立，则的取值范围是 A. B. C. D.‎ ‎12.设，函数，，，…，，曲线的最低点为，则 A. 存在，使为等腰三角形 ‎ B. 存在，使为锐角三角形 ‎ C. 存在，使为直角三角形 ‎ D. 对任意，为钝角三角形 ‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13.已知正方形的边长为2，则 .‎ ‎14.甲、乙、丙三位同学中有一人申请了北京大学的自主招生考试，当他们被问到谁申请了北京大学的自主招生考试时，甲说：丙没有申请；乙说：甲申请了；丙说：甲说对了.如果这三位同学中只有一人说的是假话，那么申请了北京大学的自主招生考试的同学是 .‎ ‎15.设函数，则满足的的取值范围是 .‎ ‎16.已知是等差数列的前项和，，则 .‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．‎ ‎17.（本小题满分10分）设是数列的前项和.已知，.‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）设，求数列的前项和.‎ ‎18.（本小题满分10分）的内角的对边分别为，已知.‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）若，的中垂线交于点，求的长.‎ ‎19.（本小题满分10分）某企业有甲、乙两套设备生产同一种产品，为了检测两套设备的生产质量情况，随机从两套设备生产的大量产品中各抽取了50件产品作为样本，检测一项质量指标值，若该项质量指标值落在内，则为合格品，否则为不合格品. 表1是甲套设备的样本的频数分布表，图1是乙套设备的样本的频率分布直方图.‎ 表1：甲套设备的样本的频数分布表 质量指标值 ‎[95,100)‎ ‎[100,105)‎ ‎[105,110)‎ ‎[110,115)‎ ‎[115,120)‎ ‎[120,125]‎ 频数 ‎1‎ ‎5‎ ‎18‎ ‎19‎ ‎6‎ ‎1‎ 图1：乙套设备的样本的频率分布直方图 ‎（Ⅰ）将频率视为概率. 若乙套设备生产了5000件产品，则其中的不合格品约有多少件；‎ ‎（Ⅱ ‎）填写下面列联表，并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关；‎ 甲套设备 乙套设备 合计 合格品 不合格品 合计 ‎（Ⅲ）根据表1和图1，对两套设备的优劣进行比较.‎ 附：‎ P(K2≥k0)‎ ‎0.15‎ ‎0.10‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎.‎ ‎20.（本题满分10分）[选修4-4：极坐标与参数方程]‎ 在直角坐标系中，直线的参数方程为（为参数），曲线的参数方程为（为参数）. 以坐标原点为极点，轴的正半轴为极轴建立极坐标系.‎ ‎（Ⅰ）求直线和曲线的极坐标方程；‎ ‎（Ⅱ）已知直线上一点的极坐标为，其中. 射线与曲线交于不同于极点的点，求的值.‎ 数学（文科） 参考答案 ‎ 一．选择题（每小题5分，共12题，共60分）‎ ‎1.B 2. C 3. B 4.D 5. A 6. C 7. D 8. D 9. B 10. C 11.A 12. D 二．填空题（每小题5分，共4小题，共20分）‎ ‎13.4 14. 乙 15. 16. ‎ 三．解答题（共6小题，共70分）‎ ‎17.解：（Ⅰ）∵，‎ ‎∴当时，，得..........................2分 当时，‎ ‎∴当时，，即..................................5分 又 ‎∴是以为首项，为公比的等比数列..................................6分 ‎∴数列的通项公式..............................................7分 ‎（Ⅱ）由（Ⅰ）知，‎ ‎∴当时，‎ ‎∴是以为首项，为公比的等比数列..............................10分 ‎∴数列的前项和为........................12分 ‎18.解：（Ⅰ）∵‎ ‎∴由正弦定理知，...................................2分 ‎∵‎ ‎∴，于是，即..............................4分 ‎∵‎ ‎∴..................................................................6分 ‎（Ⅱ）由（Ⅰ）和余弦定理知，‎ ‎∴....................................................................8分 ‎∴........................................10分 设的中垂线交于点 ‎∵在中，‎ ‎∴‎ 又 ‎∴.................................................................12分 ‎19.解：（Ⅰ）由图1知，乙套设备生产的不合格品率约为......................2分 ‎∴乙套设备生产的5000件产品中不合格品约为（件）..............3分 ‎（Ⅱ）由表1和图1得到列联表 甲套设备 乙套设备 合计 合格品 ‎48‎ ‎43‎ ‎91‎ 不合格品 ‎2‎ ‎7‎ ‎9‎ 合计 ‎50‎ ‎50‎ ‎100‎ ‎...........................................................................5分 将列联表中的数据代入公式计算得 ‎................8分 ‎∵‎ ‎∴有90%的把握认为产品的质量指标值与甲、乙两套设备的选择有关................9分 ‎（Ⅲ）由表1和图1知，甲套设备生产的合格品的概率约为，乙套设备生产的合格品的概率约为 ‎，甲套设备生产的产品的质量指标值主要集中在[105,115）之间，乙套设备生产的产品的质量指标值与甲套设备相比较为分散.因此，可以认为甲套设备生产的合格品的概率更高，且质量指标值更稳定，从而甲套设备优于乙套设备.....................12分 ‎20解：（Ⅰ）直线的普通方程为，极坐标方程为 曲线的普通方程为，极坐标方程为..............5分 ‎（Ⅱ）∵点在直线上，且点的极坐标为 ‎∴‎ ‎∵‎ ‎∴‎ ‎∴射线的极坐标方程为 联立，解得 ‎∴.....................................................10分