【数学】2020届江苏一轮复习通用版2-1函数的概念及其表示作业 6页

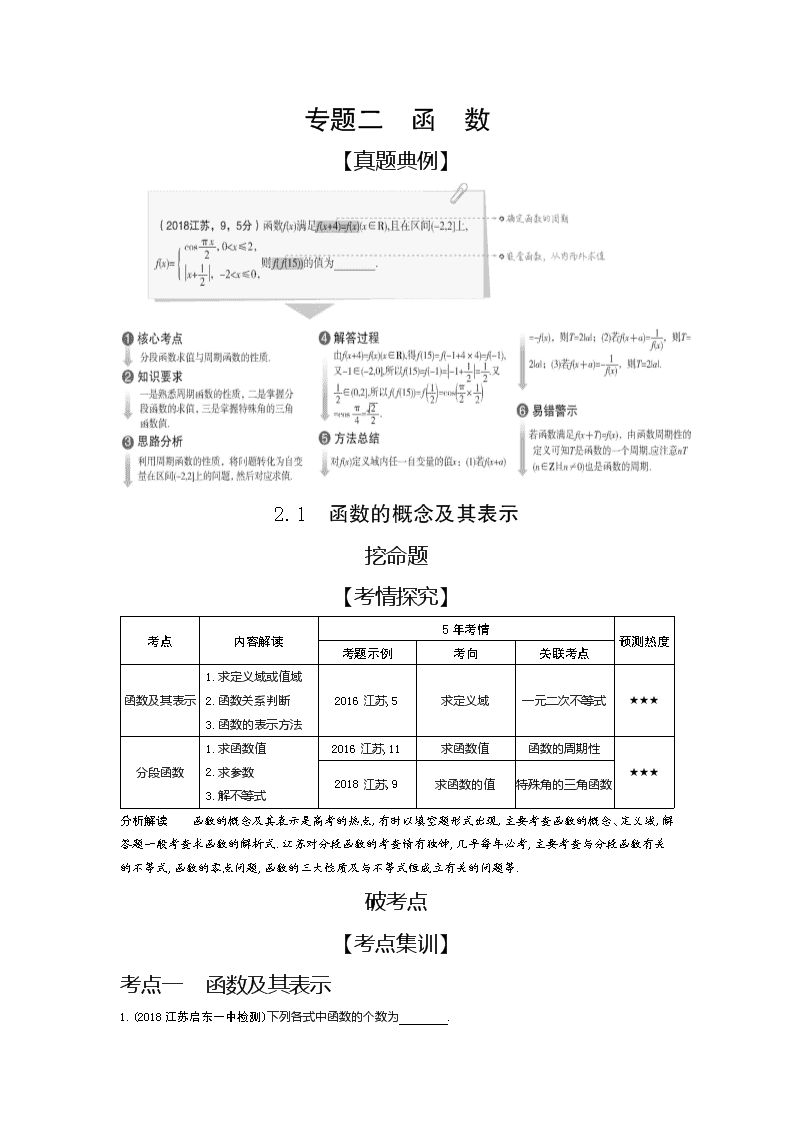
专题二　函　数 ‎【真题典例】‎ ‎2.1　函数的概念及其表示 挖命题 ‎【考情探究】‎ 考点 内容解读 ‎5年考情 预测热度 考题示例 考向 关联考点 函数及其表示 ‎1.求定义域或值域 ‎2.函数关系判断 ‎3.函数的表示方法 ‎2016江苏,5‎ 求定义域 一元二次不等式 ‎★★★‎ 分段函数 ‎1.求函数值 ‎2.求参数 ‎3.解不等式 ‎2016江苏,11‎ 求函数值 函数的周期性 ‎★★★‎ ‎2018江苏,9‎ 求函数的值 特殊角的三角函数 分析解读　　函数的概念及其表示是高考的热点,有时以填空题形式出现,主要考查函数的概念、定义域,解答题一般考查求函数的解析式.江苏对分段函数的考查情有独钟,几乎每年必考,主要考查与分段函数有关的不等式,函数的零点问题,函数的三大性质及与不等式恒成立有关的问题等.‎ 破考点 ‎【考点集训】‎ 考点一　函数及其表示 ‎1.(2018江苏启东一中检测)下列各式中函数的个数为　　　　. ‎ ‎①y=x-(x-3);②y=x-2‎+‎1-x;③y=x2;④y=±x.‎ 答案　2‎ ‎2.(2018江苏苏州高三期中调研)函数y=‎1‎ln(x-1)‎的定义域为　　　　. ‎ 答案　(1,2)∪(2,+∞)‎ ‎3.(2019届江苏盐城中学检测)已知f(x+1‎)的定义域为[0,2],则f(x)的定义域是　　　　. ‎ 答案　[1,‎3‎]‎ ‎4.已知f‎1‎x=x2+5x,则f(x)=　　　　　　. ‎ 答案　‎5x+1‎x‎2‎(x≠0)‎ ‎5.(2018江苏淮安、宿迁高三期中)已知函数f(x)与g(x)的图象关于原点对称,且它们的图象拼成如图所示的“Z”形折线段ABOCD,不含A(0,1),B(1,1),O(0,0),C(-1,-1),D(0,-1)五个点.则满足题意的f(x)的一个解析式为　　　　. ‎ 答案　f(x)=‎x,x∈(-1,0)‎‎1,x∈(0,1)‎或f(x)=‎‎-1,x∈(-1,0)‎x,x∈(0,1)‎ 考点二　分段函数 ‎1.(2019届江苏太湖高级中学检测)设函数f(x)=x‎,x≥0,‎‎-x‎,x<0,‎若f(a)+f(-1)=2,则a=　　　　. ‎ 答案　±1‎ ‎2.(2018江苏天一中学调研)f(x)是定义在R上的奇函数,当x>0时, f(x)=‎3‎x‎,00,‎则满足f(x+1)1,‎‎-x-2,x≤1,‎则函数f(x)的值域是　　　　. ‎ 答案　[-3,+∞)‎ ‎7.(2019届江苏南通中学检测)已知f(2x+1)=3x-4, f(a)=4,则a=　　　　. ‎ 答案　‎‎19‎‎3‎ ‎8.(2019届江苏无锡一中检测)已知函数F(x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,且F‎1‎‎3‎=16,F(1)=8,则F(x)的解析式为　　　　　　. ‎ 答案　F(x)=3x+‎‎5‎x ‎9.(2019届江苏梅村中学检测)若函数y=f(x)的值域是[1,3],则函数F(x)=1-2f(x+3)的值域是　　　　. ‎ 答案　[-5,-1]‎ ‎10.(2019届江苏南菁中学检测)已知函数f(x)=‎3x+2,x<1,‎x‎2‎‎+ax,x≥1,‎若f(f(0))=4a,则实数a=　　　　. ‎ 答案　2‎ 二、解答题(共20分)‎ ‎11.(2019届江苏镇江一中检测)已知f(x)=x+2,x≤-1,‎‎2x,-10,‎‎2-x,x<0.‎ ‎(1)求f(g(2))和g(f(2))的值;‎ ‎(2)求f(g(x))和g(f(x))的解析式.‎ 解析　(1)由题意可知g(2)=1, f(2)=3,‎ 因此f(g(2))=f(1)=0,‎ g(f(2))=g(3)=2.‎ ‎(2)当x>0时,g(x)=x-1,‎ 故f(g(x))=(x-1)2-1=x2-2x;‎ 当x<0时,g(x)=2-x,‎ 故f(g(x))=(2-x)2-1=x2-4x+3.‎ 所以f(g(x))=‎x‎2‎‎-2x,x>0,‎x‎2‎‎-4x+3,x<0.‎ 当x>1或x<-1时, f(x)>0,‎ 故g(f(x))=f(x)-1=x2-2;‎ 当-11或x<-1,‎‎3-x‎2‎,-1