2018届二轮复习规范答题大题突破课算法、统计与概率课件理 103页

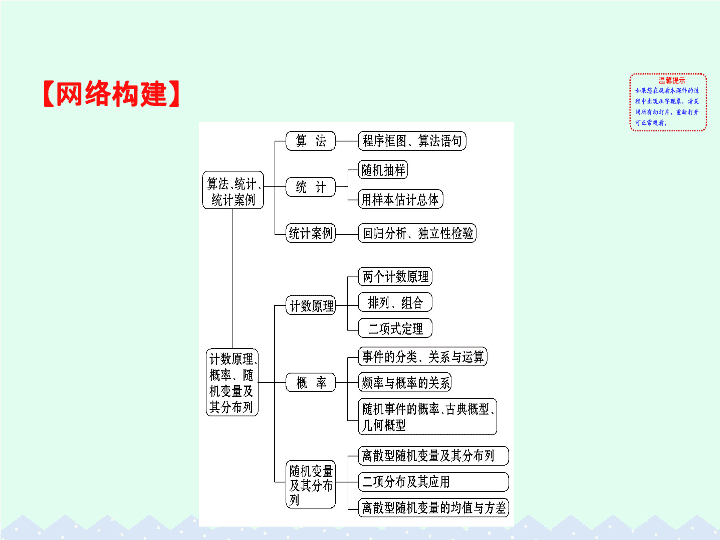
阶段总结 · 热考题型强化课 ( 六 ) 算法、统计与概率 【 网络构建 】 【 核心要素 】 1. 程序框图、算法的三种逻辑结构、算法语句 2. 简单随机抽样、系统抽样、分层抽样 3. 样本的频率分布表、频率分布直方图、茎叶图 4. 样本数据的众数、中位数、平均数、方差与标准差 5. 回归直线方程、独立性检验的步骤与计算公式 6. 事件的分类、互斥、对立、独立关系及事件间的交、并运算的概率计算公式 7. 随机事件的概率、古典概型、几何概型、条件概率的特征与计算公式 8. 分类加法与分步乘法计数原理、排列、组合的定义、排列数、组合数计算公式与应用 9. 二项式定理、通项公式及二项式系数的性质 10. 离散型随机变量的分布列及其性质 11. 两点分布、超几何分布、 n 次独立重复试验与二项分布、正态分布 12. 离散型随机变量的均值与方差 热考题型一 　算法 【 考情分析 】 难度 : 基础题 题型 : 以选择题、填空题为主 考查方式 : 以程序框图的读与补为主要考查对象 , 常与函数、不等式、数列、样本数据的数字特征等知识交汇命题 【 考题集训 】 1.(2014· 天津高考 ) 阅读如图所示的程序框图 , 运行相应的程序 , 输出 S 的值为 ( 　　 ) A.15 B.105 C.245 D.945 【 解析 】 选 B.i =1 时 ,T=3,S=3;i=2 时 ,T=5,S=15; i=3 时 ,T=7,S=105,i=4 输出 S=105. 2.(2014· 四川高考 ) 执行如图的程序框图 , 如果输入的 x,y∈R , 那么输出的 S 的最大值为 ( 　　 ) A.0 B.1 C.2 D.3 【 解析 】 选 C. 方法一 : 程序框图的实质是若 x ≥ 0,y ≥ 0, x+y≤1, 则 S=2x+y; 否则 ,S=1. 当 x≥0,y≥0,x+y≤1 时 ,0≤y≤1-x, 得 0≤x≤1, 从而 0≤2x+y≤2, 即当 x=1,y=0 时 ,S max =2×1+0=2. 方法二 : 程序框图的实质是若 x≥0,y≥0,x+y≤1, 则 S=2x+y; 否则 ,S=1. 当 时 , 如图 , 由线性规划可知 , 当 x=1,y=0 时 ,S max =2×1+0=2. 3.(2013· 重庆高考 ) 执行如图所示的程序框图 , 如果输出 s=3, 那么判断框内应填入的条件是　 ( 　　 ) A. k≤6 B.k≤7 C.k≤8 D.k≤9 【 解析 】 选 B. 第一次执行循环体后 ,s=log 2 3,k=3, 第二次执行循环体后 ,s=log 2 4,k=4, 第三次执行循环体后 ,s=log 2 5,k=5, 第四次执行循环体后 ,s=log 2 6,k=6, 第五次执行循环体后 ,s=log 2 7,k=7, 第六次执行循环体后 ,s=log 2 8=3,k=8, 结束循环 . 故选 B. 4.(2014· 山东高考 ) 执行下面的程序框图 , 若输入的 x 的值为 1, 则输出的 n 的值为 ________. 【 解析 】 根据判断条件 x 2 -4x+3≤0, 得 1≤x≤3, 输入 x=1, 第一次判断后循环 ,x=x+1=2,n=n+1=1, 第二次判断后循环 ,x=x+1=3,n=n+1=2, 第三次判断后循环 ,x=x+1=4,n=n+1=3, 第四次判断不满足条件 , 退出循环 , 输出 n=3. 答案 : 3 5.(2014· 湖北高考 ) 设 a 是一个各位数字都不是 0 且没有重复数字的三位数 . 将组成 a 的 3 个数字按从小到大排成的三位数记为 I(a ), 按从大到小排成的三位数记为 D(a )( 例如 a=815, 则 I(a )=158,D(a)=851). 阅读如图所示的程序框图 , 运行相应的程序 , 任意输入一个 a, 输出的结果 b=________. 【 解析 】 当 a=123 时 ,b=321-123=198≠123; 当 a=198 时 ,b=981-189=792≠198; 当 a=792 时 ,b=972-279=693≠792; 当 a=693 时 ,b=963-369=594≠693; 当 a=594 时 ,b=954-459=495≠594; 当 a=495 时 ,b=954-459=495=a, 终止循环 , 故输出 b=495. 答案 : 495 热考题型二 　统计与统计案例 【 考情分析 】 难度 : 低中档 题型 : 以选择题、填空题为主 , 解答题为辅 考查方式 : 以随机抽样、样本的频率分布表、频率分布直方图、茎叶图及平均数、方差、标准差、线性回归方程、独立性检验为主要考查对象 , 常以统计图表为载体 , 综合考查以上知识点 【 考题集训 】 1.(2014· 广东高考 ) 已知某地区中小学生人数和近视情况分别如图 1 和图 2 所示 , 为了解该地区中小学生的近视形成原因 , 用分层抽样的方法抽取 2% 的学生进行调查 , 则样本容量和抽取的高中生近视人数分别是　 ( 　　 ) A.200,20 B.100,20 C.200,10 D.100,10 【 解析 】 选 A. 样本容量为 10000 × 2%=200, 抽取的高中生近视人数为 2000 × 2% × 50%=20. 2.(2013· 重庆高考 ) 如图茎叶图记录了甲、乙两组各 5 名学生在一次英语听力测试中的成绩 ( 单位 : 分 ). 已知甲组数据的中位数为 15, 乙组数据的平均数为 16.8, 则 x,y 的值分别为　 ( 　　 ) A.2,5 B.5,5 C.5,8 D.8,8 【 解析 】 选 C. 因为甲组数据的中位数为 15, 所以易知 x=5, 又乙组数据的平均数为 16.8, 所以 =16.8, 解得 y=8. 故选 C. 3.(2013· 江苏高考 ) 抽样统计甲、乙两位射击运动员的 5 次训练成绩 ( 单位 : 环 ), 结果如下 : 则成绩较为稳定 ( 方差较小 ) 的那位运动员成绩的方差为 ________. 运动员 第一次 第二次 第三次 第四次 第五次 甲 87 91 90 89 93 乙 89 90 91 88 92 【 解析 】 故 答案： 2 4.(2014· 新课标全国卷 Ⅱ) 某地区 2007 年至 2013 年农村居民家庭纯收入 y( 单位 : 千元 ) 的数据如下表 : (1) 求 y 关于 t 的线性回归方程 . 年份 2007 2008 2009 2010 2011 2012 2013 年份代号 t 1 2 3 4 5 6 7 人均纯收入 y 2.9 3.3 3.6 4.4 4.8 5.2 5.9 (2) 利用 (1) 中的回归方程 , 分析 2007 年至 2013 年该地区农村居民家庭人均纯收入的变化情况 , 并预测该地区 2015 年农村居民家庭人均纯收入 . 附 : 回归直线的斜率和截距的最小二乘法估计公式分别为 : 【 解析 】 (1) 因为 设回归方程为 代入公式，经计算得 所以 y 关于 t 的回归方程为 y= t+2.3. (2) 因为 >0, 所以 2007 年至 2013 年该地区人均纯收入稳步增长，预计到 2015 年，该地区人均纯收入 y= ×9+2.3=6.8( 千元 ) ， 所以预计到 2015 年，该地区人均纯收入约 6 800 元 . 5.(2014· 安徽高考 ) 某高校共有学生 15000 人 , 其中男生 10500 人 , 女生 4500 人 , 为调查该校学生每周平均体育运动时间的情况 , 采用分层抽样的方法 , 收集 300 位学生每周平均体育运动时间的样本数据 ( 单位 : 小时 ). (1) 应收集多少位女生的样本数据 ? (2) 根据这 300 个样本数据 , 得到学生每周平均体育运动时间的频率分布直方图 ( 如图所示 ), 其中样本数据的分组区间为 :[0,2],(2,4],(4,6],(6,8],(8,10],(10,12]. 估计该校学生每周平均体育运动时间超过 4 小时的概率 . (3) 在样本数据中 , 有 60 位女生的每周平均体育运动时间超过 4 小时 . 请完成每周平均体育运动时间与性别的列联表 , 并判断是否有 95% 的把握 ( 在犯错误的概率不超过 0.05 的前提下 ) 认为“该校学生的每周平均体育运动时间与性别有关” . 【 解析 】 (1)300 × =90, 所以应收集 90 位女生的样本数据 . (2) 由频率分布直方图得 2×(0.150+0.125+0.075+ 0.025)=0.75, 所以该校学生每周平均体育运动时间超过 4 小时的概率的估计值为 0.75. (3) 由 (2) 知 ,300 位学生中有 300×0.75=225 人的每周平均体育运动时间超过 4 个小时 .75 人的每周平均体育运动时间不超过 4 个小时 . 又因为样本数据中有 210 份是关于男生的 ,90 份是关于女生的 , 所以每周平均体育运动时间与性别的列联表如下 : 平均体育运动时间与性别列联表 男生 女生 总计 每周平均体育运动时间 不超过 4 个小时 45 30 75 每周平均体育运动时间 超过 4 个小时 165 60 225 总计 210 90 300 结合列联表可算得 K 2 的观测值 k= ≈4.762>3.841. 有 95% 的把握 ( 在犯错误的概率不超过 0.05 的前提下 ) 认为“该校学生的每周平均体育运动时间与性别有关” . 热考题型三 　概率的计算 【 考情分析 】 难度 : 基础题 题型 : 以选择题、填空题为主 考查方式 : 以古典概型、几何概型、条件概率、互斥事件的和事件的概率、对立事件的概率、相互独立事件的积事件的概率、二项分布等为主要考查对象 , 常与排列、组合、函数、方程、不等式、数列、解析几何、线性规划、定积分等知识综合命题 【 考题集训 】 1.(2014· 陕西高考 ) 从正方形四个顶点及其中心这 5 个点中 , 任取 2 个点 , 则这 2 个点的距离不小于该正方形边长的概率为　 ( 　　 ) 【 解析 】 选 C. 从边长为 1 的正方形的中心和 顶点这五点中 , 随机 ( 等可能 ) 取两点 , 共有 =10 条线段 , 满足该两点间的距离不小于 1 的有 AB,BC,CD,DA,AC,BD 共 6 条线段 , 则根据古典概型的 概率公式可知随机 ( 等可能 ) 取两点 , 则该两点间的距离 不小于 1 的概率 P= 2.(2014· 湖北高考 ) 由不等式组 确定的平面区域记为 Ω 1 , 不等式组 确定的平面区域记为 Ω 2 , 在 Ω 1 中随机取一点 , 则该点恰好在 Ω 2 内的概率为　 ( 　　 ) 【 解析 】 选 D. 依题意 , 不等式组表示的平面区域如图 , 由几何概型概率公式知 , 该点落在 Ω 2 内的概率为 3.(2014· 全国卷 Ⅱ) 某地区空气质量监测资料表明 , 一天的空气质量为优良的概率是 0.75, 连续两天为优良的概率是 0.6, 已知某天的空气质量为优良 , 则随后一天的空气质量为优良的概率是　 ( 　　 ) A.0.8 B.0.75 C.0.6 D.0.45 【 解析 】 选 A. 设某天空气质量优良 , 则随后一天空气质量也优良的概率为 p, 则据题有 0.6=0.75 · p, 解得 p=0.8, 故选 A. 4.(2013· 山东高考 ) 甲、乙两支排球队进行比赛 , 约定 先胜 3 局者获得比赛的胜利 , 比赛随即结束 . 除第五局甲 队获胜的概率是 外 , 其余每局比赛甲队获胜的概率是 . 假设每局比赛结果互相独立 . (1) 分别求甲队以 3∶0,3∶1,3∶2 胜利的概率 . (2) 若比赛结果为 3∶0 或 3∶1, 则胜利方得 3 分 , 对方得 0 分 ; 若比赛结果为 3∶2, 则胜利方得 2 分、对方得 1 分 , 求乙队得分 X 的分布列及数学期望 . 【 解析 】 (1) 记“甲队以 3∶0 胜利”为事件 A 1 ,“ 甲队 以 3∶1 胜利”为事件 A 2 ,“ 甲队以 3∶2 胜利”为事件 A 3 , 由题意 , 各局比赛结果相互独立 , 故 P(A 1 )= ,P(A 2 )= P(A 3 )= 所以甲队以 3∶0 胜利、以 3∶1 胜利的概率都为 , 甲 队以 3∶2 胜利的概率为 . (2) 设“乙队以 3∶2 胜利”为事件 A 4 , 由题意 , 各局比赛结果相互独立 , 所以 P(A 4 )= 由题意 , 随机变量 Χ 的所有可能的取值为 0,1,2,3, 根据事件的互斥性得 P(Χ=0)=P(A 1 +A 2 )=P(A 1 )+P(A 2 )= 又 P(Χ=1)=P(A 3 )= P(Χ=2)=P(A 4 )= P(Χ=3)=1-P(Χ=0)-P(Χ=1)-P(Χ=2)= 故 Χ 的分布列为 X 0 1 2 3 P 所以 E(Χ)= 5.(2014· 安徽高考 ) 甲、乙两人进行围棋比赛，约定 先连胜两局者直接赢得比赛，若赛完 5 局仍未出现连 胜，则判定获胜局数多者赢得比赛，假设每局甲获胜 的概率为 ，乙获胜的概率为 ，各局比赛结果相互 独立 . (1) 求甲在 4 局以内 ( 含 4 局 ) 赢得比赛的概率 . (2) 记 X 为比赛决出胜负时的总局数，求 X 的分布列和均值 ( 数学期望 ). 【 解析 】 A i 表示“第 i 局甲获胜” ,B i 表示“第 i 局乙获胜” , 则 P(A i )= ,P(B i )= ,i=1,2,3,4,5. (1) 用 A 表示“甲在 4 局以内 ( 含 4 局 ) 赢得比赛” , P(A)=P(A 1 A 2 )+P(B 1 A 2 A 3 )+P(A 1 B 2 A 3 A 4 ) =P(A 1 )P(A 2 )+P(B 1 )P(A 2 )P(A 3 )+P(A 1 )P(B 2 )P(A 3 )P(A 4 ) (2)X 的可能取值为 2,3,4,5. P(X=2)=P(A 1 A 2 )+P(B 1 B 2 ) =P(A 1 )P(A 2 )+P(B 1 )P(B 2 )= P(X=3)=P(B 1 A 2 A 3 )+P(A 1 B 2 B 3 )= P(X=4)=P(A 1 B 2 A 3 A 4 )+P(B 1 A 2 B 3 B 4 )= P(X=5)=1-P(X=2)-P(X=3)-P(X=4)= 故 X 的分布列为： E(X)= X 2 3 4 5 P 热考题型四 　概率与统计、统计案例的综合 【 考情分析 】 难度 : 低中档 题型 : 以解答题为主 考查方式 : 常以统计图表为载体 , 考查随机抽样、用样本频率分布估计总体、样本的数字特征、回归分析、独立性检验及概率的计算问题 【 考题集训 】 1.(2014· 全国卷 Ⅱ) 某市为了考核甲、乙两部门的工作情况 , 随机访问了 50 位市民 . 根据这 50 位市民对这两部门的评分 ( 评分越高表示市民的评价越高 ), 绘制茎叶图如下 : (1) 分别估计该市的市民对甲、乙部门评分的中位数 . (2) 分别估计该市的市民对甲、乙部门的评分小于 90 的概率 . (3) 根据茎叶图分析该市的市民对甲、乙两部门的评价 . 【 解析 】 (1) 两组数字是有序排列的 ,50 个数的中位数 为第 25,26 两个数的平均数 . 由给出的数据可知道 , 市民 对甲部门评分的中位数为 =75, 对乙部门评分的 中位数为 =67, 所以市民对甲、乙两部门评分的 中位数分别为 75,67. (2) 甲部门评分数大于等于 90 的共有 6 个、乙部门评分数大于等于 90 的共有 9 个 . 因此 , 估计市民对甲、乙部门的评分大于等于 90 的概率分别为 P 甲 = =0.12,P 乙 = =0.18. 所以市民对甲、乙部门的评分小于 90 的概率分别为 0.88,0.82. (3) 由所给茎叶图知 , 市民对甲部门的评分的中位数高于对乙部门的评分的中位数 , 而且由茎叶图可以大致看出对甲部门的评分的标准差要小于对乙部门的评分的标准差 , 说明该市市民对甲部门的评价较高、评价较为一致 , 对乙部门的评价较低、评价差异较大 . 2.(2014· 辽宁高考 ) 某大学餐饮中心为了解新生的饮食习惯 , 在全校一年级学生中进行了抽样调查 , 调查结果如下表所示 : 喜欢甜品 不喜欢甜品 合计 南方学生 60 20 80 北方学生 10 10 20 合计 70 30 100 (1) 根据表中数据 , 问是否有 95% 的把握 ( 在犯错误的概率不超过 0.05 的前提下 ) 认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异” . (2) 已知在被调查的北方学生中有 5 名数学系的学生 , 其中 2 名喜欢甜品 , 现在从这 5 名学生中随机抽取 3 人 , 求至多有 1 人喜欢甜品的概率 . 【 解析 】 (1) 由 2 × 2 列联表中的数据 , 得 K 2 = ≈4.762, 由于 4.762>3.841, 所以有 95% 的把握 ( 在犯错误的概率不超过 0.05 的前提下 ) 认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异” . (2) 从 5 名数学系学生中抽取 3 人的一切可能结果所组成 的基本事件为下列 10 个 : (a 1 ,a 2 ,b 1 ),(a 1 ,a 2 ,b 2 ),(a 1 ,a 2 ,b 3 ),(a 1 ,b 1 ,b 2 ),(a 1 ,b 1 , b 3 ),(a 1 ,b 2 ,b 3 ),(a 2 ,b 1 ,b 2 ),(a 2 ,b 1 ,b 3 ),(a 2 ,b 2 ,b 3 ), (b 1 ,b 2 ,b 3 ), 其中 a i (i =1,2) 表示喜欢甜品的学生 ,b j (j =1,2,3) 表示 不喜欢甜品的学生 , 这 10 个基本事件的出现是等可能的 . 抽取 3 人 , 至多有 1 人喜欢甜品的事件为以下 7 个 : (a 1 ,b 1 ,b 2 ),(a 1 ,b 1 ,b 3 ),(a 1 ,b 2 ,b 3 ),(a 2 ,b 1 ,b 2 ),(a 2 ,b 1 , b 3 ),(a 2 ,b 2 ,b 3 ),(b 1 ,b 2 ,b 3 ), 从这 5 名学生中随机抽取 3 人 , 至多有 1 人喜欢甜品的概 率为 . 3.(2014· 全国卷 Ⅰ) 从某企业生产的某种产品中抽取 500 件 , 测量这些产品的一项质量指标值 , 由测量结果得如下频率分布直方图 : (1) 求这 500 件产品质量指标值的样本平均数和样本方 差 s 2 ( 同一组中的数据用该组区间的中点值作代表 ). (2) 由直方图可以认为 , 这种产品的质量指标值 Z 服从正 态分布 N(μ,σ 2 ), 其中 μ 近似为样本平均数 ,σ 2 近 似为样本方差 s 2 . ① 利用该正态分布 , 求 P(187.8120 发电机最多 可运行台数 1 2 3 若某台发电机运行 , 则该台年利润为 5000 万元 ; 若某台发电机未运行 , 则该台年亏损 800 万元 , 欲使水电站年利润的均值达到最大 , 应安装发电机多少台 ? 【 解析 】 (1) 依题意 ,p 1 =P(40120)= =0.1. 根据二项分布 , 在未来 4 年中至多有 1 年的年入流量超过 120 的概率为 (2) 记水电站年总利润为 Y, ① 安装 1 台发电机的情形 : 由于水库年入流量总大于 40, 故一台发电机运行的概率为 1, 对应的年利润 Y=5000,E(Y)=1×5000=5000. ②安装 2 台发电机的情形 : 依题意 , 当 40120 时 , 三台发电机运行 , 此时 Y=5000×3=15000, 因此 P(Y=15000)=P(X>120)=p 3 =0.1. 由此得分布列如下 所以 ,E(Y)=3400×0.2+9200×0.7+15000×0.1=8620. 综上 , 欲使水电站年总利润的均值达到最大 , 应安装发电机 2 台 . Y 3 400 9 200 15 000 P 0.2 0.7 0.1 3.(2013· 安徽高考 ) 某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动 , 分别由李老师和张老师负责 , 已知该系共有 n 位学生 , 每次活动均需该系 k 位学生参加 (n 和 k 都是固定的正整数 ). 假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系 k 位学生 , 且所发信息都能收到 . 记该系收到李老师或张老师所发活动通知信息的学生人数为 X. (1) 求该系学生甲收到李老师或张老师所发活动通知信息的概率 . (2) 求使 P(X=m) 取得最大值的整数 m. 【 解析 】 (1) 因为事件 A:“ 学生甲收到李老师所发 信息”与事件 B:“ 学生甲收到张老师所发信息”是 相互独立的事件 , 所以 与 相互独立 , 由于 P(A)=P(B)= , 故 P( )=P( )=1- , 因此 P=1- (2) 当 k=n 时 ,m 只能取 n, 有 P(X=m)=P(X=n)=1, 当 k