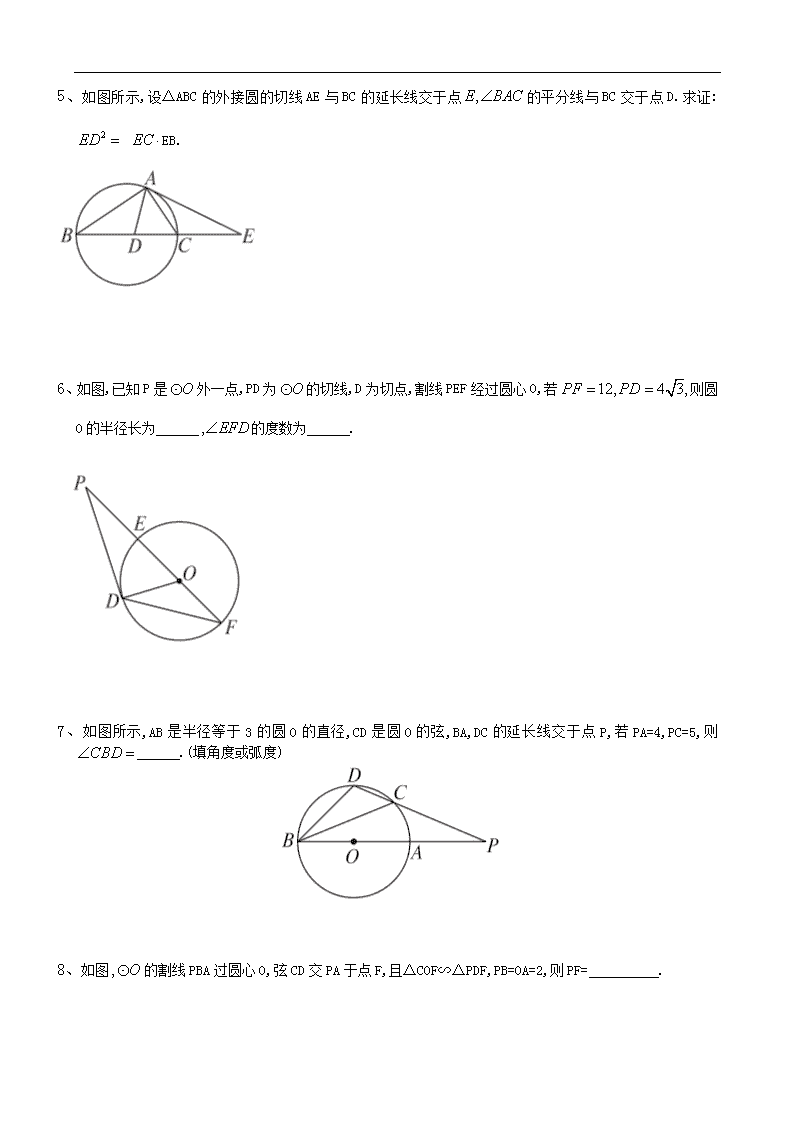2013届高考数学一轮复习 直线与圆的位置关系 10页

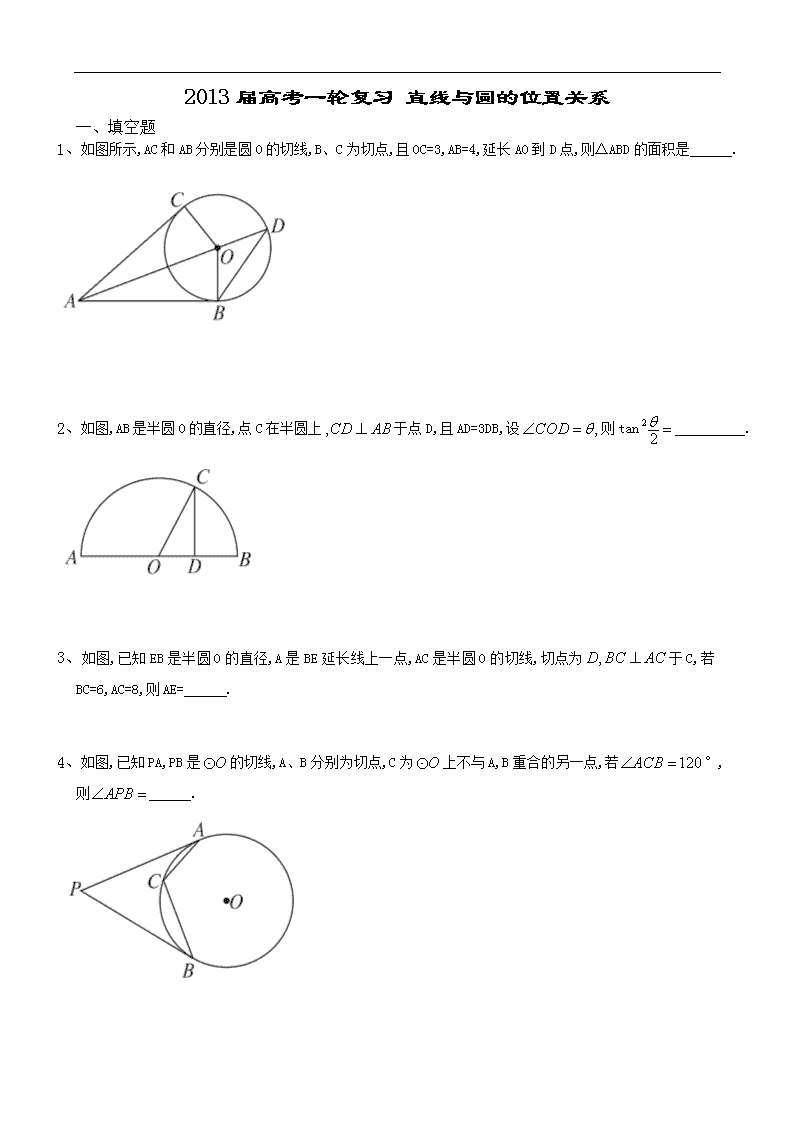
‎2013届高考一轮复习 直线与圆的位置关系 一、填空题 ‎1、如图所示,AC和AB分别是圆O的切线,B、C为切点,且OC=3,AB=4,延长AO到D点,则△ABD的面积是 . ‎ ‎2、如图,AB是半圆O的直径,点C在半圆上于点D,且AD=3DB,设则tan . ‎ ‎3、如图,已知EB是半圆O的直径,A是BE延长线上一点,AC是半圆O的切线,切点为于C,若BC=6,AC=8,则AE= . ‎ ‎4、如图,已知PA,PB是的切线,A、B分别为切点,C为上不与A,B重合的另一点,若°,则 . ‎ ‎5、如图所示,设△ABC的外接圆的切线AE与BC的延长线交于点的平分线与BC交于点D.求证: EB. ‎ ‎6、如图,已知P是外一点,PD为的切线,D为切点,割线PEF经过圆心O,若则圆O的半径长为 的度数为 . ‎ ‎7、如图所示,AB是半径等于3的圆O的直径,CD是圆O的弦,BA,DC的延长线交于点P,若PA=4,PC=5,则 .(填角度或弧度) ‎ ‎ ‎ ‎8、如图的割线PBA过圆心O,弦CD交PA于点F,且△COF∽△PDF,PB=OA=2,则PF= . 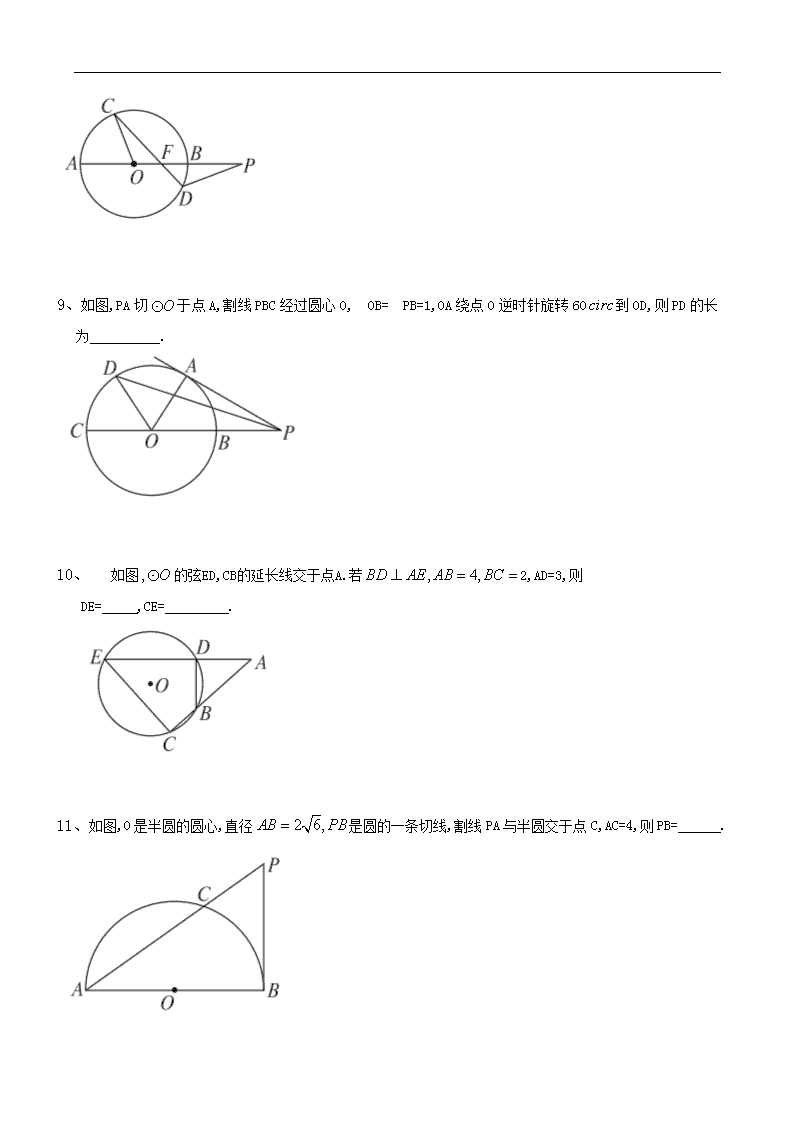‎ ‎9、如图,PA切于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转60到OD,则PD的长为 . ‎ ‎10、 如图的弦ED,CB的延长线交于点A.若2,AD=3,则 DE= ,CE= . ‎ ‎11、如图,O是半圆的圆心,直径是圆的一条切线,割线PA与半圆交于点C,AC=4,则PB= . ‎ ‎12、如图,已知PA是的切线,A是切点,直线PO交于B、C两点,D是OC的中点,连接AD并延长交于点E.若°,则AE= . ‎ ‎13、如图,圆内的两条弦AB、CD相交于圆内一点P,已知PA则CD= . ‎ 二、解答题 ‎14、从外一点P引圆的两条切线PA,PB及一条割线PCD,A,B为切点.求证:. ‎ ‎15、如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD. ‎ ‎(1)求BD的长; ‎ ‎(2)求的度数; ‎ ‎(3)求的值. ‎ ‎16、如图的直径AB=4,C为圆周上一点,AC=2,过点C作的切线l,过点B作l的垂线BD,垂足为D,BD与交于点E. ‎ ‎(1)求的度数; ‎ ‎(2)求证:四边形OBEC是菱形. ‎ 以下是答案 一、填空题 ‎1、 ‎ 解析:由题知AB=AC. ‎ ‎∵∴AO=5. ‎ ∴sinsin=. ‎ ‎2、 ‎ 解析:tantantan. ‎ ‎3、 ‎ 解析:设圆的半径为R,连接 ‎10-. ‎ ‎4、60° ‎ 解析:连接AO,BO,由°,得所对的弧为240°, ‎ ‎∴°,又°,得°. ‎ ‎5、证明:因为AE是圆的切线, ‎ 所以. ‎ 又因为AD是的平分线,所以. ‎ 从而. ‎ 因为 ‎ ‎ ‎ 所以故EA=ED. ‎ 因为EA是圆的切线,所以由切割线定理知, ‎ 而EA=ED,所以. ‎ ‎6、4 30° ‎ 解析:连接DE,由切割线定理得. ‎ ‎∴EF=8,OD=4.∵ ‎ ‎∴°,∴°. ‎ ‎7、 30°(或 ‎ 解析:由割线定理知:即10=5(DC+5),解得DC=3,所以△DOC是正三角形,所以°,而°.‎ ‎8、3 ‎ 解析:令OF=x,则即(x+2)(2-x)=x(2+2-x),x=1,所以PF=3. ‎ ‎9、 ‎ 解析:∵PA切于点A,B为PO中点,∴AB=OB=OA,∴°,∴°,在△POD中由余弦定理,得:DOcos.∴. ‎ ‎10、5 ‎ 解析:首先由割线定理不难知道于是AE=8,DE=5.又故BE为直径,因此°,由勾股定理可知故. ‎ ‎11、 ‎ 解析:由射影定理得. ‎ ‎12、 ‎ 解析:连接tan 30°,AO=2,PB=2,由余弦定理得cos 30°‎ ‎=7,所以.由相交弦定理得所以. ‎ ‎13、 ‎ 解析:由相交弦定理可得 ‎ ∴9,即 ‎ ‎∴. ‎ 二、解答题 ‎14、证明:∵PA为的切线, ‎ ‎∴ ‎ 而∴△PAC∽△PDA, ‎ 则.同理可得. ‎ ‎∵PA=PB,∴ ‎ ‎∴. ‎ ‎15、解:(1)连接OC,OB,AE,并延长BO交AE于点H, ‎ ‎∵AB是小圆的切线,C是切点, ‎ ‎∴ ‎ ‎∴C是AB的中点. ‎ ‎∵AD是大圆的直径, ‎ ‎∴O是AD的中点. ‎ ‎∴OC是△ABD的中位线. ‎ ‎∴BD=2OC=10. ‎ ‎(2)由(1)知C是AB的中点. ‎ 同理F是BE的中点. ‎ 由切线长定理得BC=BF. ‎ ‎∴BA=BE. ‎ ‎∴. ‎ ‎∵ ‎ ‎∴°. ‎ ‎(3)在Rt△OCB中, ‎ ‎∵OB=13,OC=5, ‎ ‎∴BC=12. ‎ 由(2)知. ‎ ‎∵ ‎ ‎∴△O∽△AGB. ‎ ‎. ‎ ‎16、(1)解:在△AOC中,AC=2, ‎ ‎∵AO=OC=2, ∴△AOC是等边三角形. ‎ ‎∴°, ‎ ‎∴°. ‎ ‎(2)证明:∵. ‎ ‎∴OC∥BD. ‎ ‎∴°. ‎ ‎∵AB为的直径, ‎ ‎∴△AEB为直角三角形°. ‎ ‎∴. ‎ ‎∴四边形OBEC为平行四边形. ‎ 又∵OB=OC=2. ‎ ‎∴四边形OBEC是菱形.‎