新疆乌鲁木齐地区2020届高三年级第一次质量检监测文科数学试题 20页

乌鲁木齐地区2020年高三年级第一次质最监测 文科数学(问卷)‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题：本大题共12个小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.若集合，，则集合（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 解二次不等式，求得集合，再求集合交集即可.‎ ‎【详解】对集合：，解得.‎ 根据集合的交运算可得：‎ ‎.‎ 故选：A.‎ ‎【点睛】本题考查集合交集的运算，涉及简单二次不等式的求解，属基础题.‎ ‎2.已知复数（是虚数单位），则的共轭复数（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据复数的乘法运算，求得复数，再求其共轭复数即可.‎ ‎【详解】因为，‎ 故可得，‎ 故.‎ 故选：C.‎ ‎【点睛】本题考查复数的乘法运算以及共轭复数的求解，属基础题.‎ ‎3.已知双曲线（，）的两条渐近线互相垂直，焦距为，则该双曲线的实轴长为（ ）‎ A. 3 B. ‎6 ‎C. 9 D. 12‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据渐近线垂直，可得的关系，结合焦距的长度，列方程组，即可求得结果.‎ ‎【详解】因为两条渐近线互相垂直，故可得，‎ 又因为焦距为，故可得，‎ 结合，‎ 解得，‎ 故实轴长.‎ 故选：B.‎ ‎【点睛】本题考查双曲线方程的求解，属基础题.‎ ‎4.已知，为两条不同的直线，，，为三个不同的平面，则下列命题正确的是（ ）‎ A. 若，，则 B. 若，且，则 C. 若，，，，则 D. 若，，，则 ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据线线平行，线线垂直，线面垂直，面面垂直的判定，对选项进行逐一分析即可.‎ ‎【详解】对：若，，则，或与是异面直线，或与相交，故错误；‎ 对：若，且，‎ ‎ 不妨取交线上一点，作平面的垂线为，‎ ‎ 因为，且点，故；‎ ‎ 同理可得，故与是同一条直线，‎ ‎ 因为，故.‎ ‎ 故选项正确.‎ 对：只有当与是相交直线时，若，，，，‎ 才会有.故错误；‎ 对：若，，，则与的关系不确定，故错误.‎ 故选：B.‎ ‎【点睛】本题考查线线平行，面面平行，面面垂直的判定，属综合基础题.‎ ‎5.数列是公差为2的等差数列，为其前项和，且，，成等比数列，则（ ）‎ A. 8 B. ‎12 ‎C. 16 D. 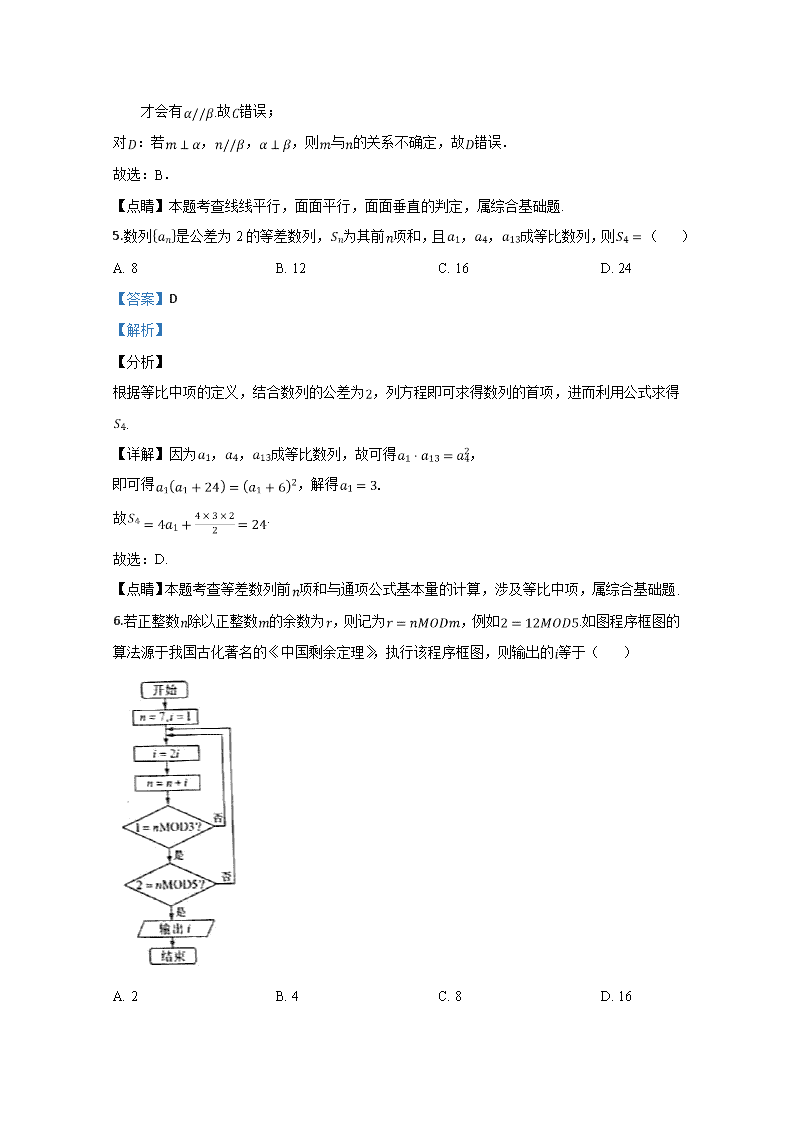24‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据等比中项的定义，结合数列的公差为，列方程即可求得数列的首项，进而利用公式求得.‎ ‎【详解】因为，，成等比数列，故可得，‎ 即可得，解得.‎ 故.‎ 故选：D.‎ ‎【点睛】本题考查等差数列前项和与通项公式基本量的计算，涉及等比中项，属综合基础题.‎ ‎6.若正整数除以正整数的余数为，则记为，例如.如图程序框图的算法源于我国古化著名的《中国剩余定理》，执行该程序框图，则输出的等于（ ）‎ A. 2 B. ‎4 ‎C. 8 D. 16‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 模拟执行程序，根据循环结构，逐步执行，即可得到结果.‎ ‎【详解】‎ 模拟执行程序如下：‎ 开始，‎ ‎，不满足，‎ 故，满足，但不满足，‎ 故，不满足，‎ 故，满足，满足，‎ 输出.‎ 故选：D.‎ ‎【点睛】本题考查循环结构语句的执行，只需按照程序框图模拟执行即可，属基础题.‎ ‎7.为了解某市居民用水情况，通过抽样，获得了100位居民某年的月均用水量(单位：吨).将数据按照，…，分成9组，绘制了如图所示的频率分布直方图.政府要试行居民用水定额管理，制定一个用水量标准.使的居民用水量不超过，按平价收水费，超出 的部分按议价收费，则以下比较适合做为标准的是（ ）‎ A. 2.5‎吨 B. 3吨 C. 3.5吨 D. 4吨 ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据频率分布直方图中，长方形面积表示频率，找出将面积分割为和的数值，即为标准.‎ ‎【详解】根据频率分布直方图，结合题意可得：‎ 解得.‎ 故要满足的居民用水量不超过，‎ 则比较合适的取值为吨.‎ 故选：B.‎ ‎【点睛】本题考查频率分布直方图中，频率的计算，属基础题.‎ ‎8.天文学中为了衡量星星的明暗程度，古希腊天文学家喜帕恰斯(，又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小，星星就越亮；星等的数值越大，它的光就越暗.到了1850年，由于光度计在天体光度测量中的应用，英国天文学家普森()又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足.其中星等为的星的亮度为.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的倍，则与最接近的是(当较小时， )‎ A. 1.24 ‎B. ‎1.25 ‎C. 1.26 D. 1.27‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据题意，代值计算，即可得，再结合参考公式，即可估算出结果.‎ ‎【详解】根据题意可得：‎ 可得，解得，‎ 根据参考公式可得，‎ 故与最接近的是.‎ 故选：C.‎ ‎【点睛】本题考查对数运算，以及数据的估算，属基础题.‎ ‎9.已知函数在上单调递增，则的最大值为（ ）‎ A. 1 B. ‎2 ‎C. 4 D. 6‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 求出的取值范围，结合正弦函数的单调区间，即可求得.‎ ‎【详解】因为，故可得，‎ 又的单调增区间为，‎ 故当时，只需是的子集即可.‎ 则：，解得，‎ 故的最大值为.‎ 故选：C.‎ ‎【点睛】本题考查由正弦型三角函数的单调区间，求参数的取值范围，属中档题.‎ ‎10.已知，，，，则，，的大小关系是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 因为，故可得，由指数函数和幂函数的单调性即可比较大小.‎ ‎【详解】因为，故可得，‎ 根据指数函数是单调减函数，‎ 可得，即可得；‎ 根据幂函数是单调增函数，‎ 可得，即可得 综上所述：.‎ 故选：A.‎ ‎【点睛】本题考查正弦函数和余弦函数在区间上的大小关系，以及指数函数和幂函数的单调性，属综合中档题.‎ ‎11.已知抛物线的焦点为，准线为，过点且斜率为的直线交抛物线于点（在第一象限），于点，直线交轴于点，则（ ）‎ A. 4 B. C. 2 D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 设出直线方程，联立抛物线方程，求得点的坐标，即可得点坐标，进而可求得的方程，容易得点的坐标，用两点之间的距离公式即可求得的长度.‎ ‎【详解】根据题意，作图如下：‎ 由题可知，点，故直线的方程为，‎ 联立抛物线方程 可得，解得或 因为点在第一象限，故可得.‎ 又因为准线方程为，故可得.‎ 则直线的方程为，‎ 令，解得，即可得.‎ 故.‎ 故选：B.‎ ‎【点睛】本题考查抛物线中线段长度的求解，关键是要逐步求解出点的坐标即可.‎ ‎12.已知函数，若，则的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据函数的单调性，得到满足题意的的范围，根据，得到与之间的关系，构造关于的函数，求该函数的值域即可.‎ ‎【详解】根据题意，因为是单调递增函数，也是单调增函数，‎ 且，故在整个定义域上都是单调增函数.‎ 当且仅当时，满足题意，‎ 否则不妨令，要满足题意，则有.‎ 又因为，故可得，‎ 解得，‎ 故，‎ 令，‎ 则，令，解得，‎ 故函数在区间上单调递减，在区间上单调递增，‎ 故，没有最大值.‎ 综上所述：故的取值范围为.‎ 故选：A.‎ ‎【点睛】本题考查利用导数求函数的值域，以及分段函数的单调性，属综合性中档题.‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.已知单位向量，满足，则向量与向量夹角的大小为__________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据向量的数量积运算，结合单位向量模长为1，代值计算即可.‎ ‎【详解】因为，均是单位向量，故可得，‎ 故可得，‎ 即，解得，‎ 又因为向量夹角的范围为，‎ 故的夹角为.‎ 故答案为：.‎ ‎【点睛】本题考查向量数量积的运算，属基础题.‎ ‎14.已知圆的圆心为，点在直线上，则的最小值为__________．‎ ‎【答案】3‎ ‎【解析】‎ ‎【分析】‎ 根据直线和圆相离，即可得圆心到直线的距离减去半径，即为所求.‎ ‎【详解】因为圆方程为，故，‎ 则圆心到直线的距离，则直线与圆相离.‎ 故得最小值为.‎ 故答案为：3.‎ ‎【点睛】本题考查圆心到直线上一点距离的最值问题，属基础题.‎ ‎15.造纸术是我国古代四大发明之一，纸张的规格是指纸张制成后，经过修整切边，裁成一定的尺寸.现在我国采用国际标准，规定以、、…、；、、…、等标记来表示纸张的幅面规格.复印纸幅面规格只采用系列和系列，共中系列的幅面规格为：①规格的纸张的幅宽(以表示)和长度(以表示)的比例关系为；②将纸张沿长度方向对开成两等分，便成为规格，纸张沿长度方向对开成两等分，便成为规格，…，如此对开至规格.现有、、、…、纸各一张.若纸的面积为.则这9张纸的面积之和等于__________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据题意，求出纸张的长度和宽度，构造纸张面积的等比数列，利用等比数列前项和的计算公式，即可求得.‎ ‎【详解】由题可设，纸的面积为，‎ 根据题意，纸张面积是首项为，公比为的等比数列，‎ 则容易知纸张的面积为，故可得，‎ 故纸张面积是一个首项为，公比为的等比数列，‎ 故张纸的面积之和为.‎ 故答案为：.‎ ‎【点睛】本题考查实际问题中等比数列的应用，问题的关键是要构造等比数列，属中档题.‎ ‎16.如图，关于正方体，有下列四个命题：‎ ‎①与平面所成角为45°；‎ ‎②三棱锥与三棱锥的体积比为；‎ ‎③存在唯一平面.使平面且截此正方体所得截面为正六边形；‎ ‎④过作平面，使得棱、，在平面上的正投影的长度相等.则这样的平面 有且仅有一个.‎ 上述四个命题中，正确命题的序号为________.‎ ‎【答案】①②③.‎ ‎【解析】‎ ‎【分析】‎ 根据线面角的求解方法，三棱锥体积计算公式，正方体截面的性质，以及投影的相关知识，对选项进行逐一分析即可.‎ ‎【详解】对①：过作垂直于，垂足为，如下图所示：‎ 因为是正方体，‎ 容易知平面，且平面，故可得，‎ 又因为，故平面，故即为所求线面角.‎ 容易知为等腰直角三角形，故.‎ 即与平面所成角为45°.故①正确；‎ 对②：设正方体棱长为1，‎ 故可得；‎ 而棱锥的体积可以理解为 正方体体积减去4个体积都和相等的三棱锥的体积，‎ 故.‎ 故棱锥与三棱锥的体积比为，则②正确；‎ 对③：根据正方体截面的性质，当截面为六边形时，‎ 当且仅当为各点所在棱的中点时，截面为正六边形，如下图所示：‎ 其它情况下，无法保证截面六边形的棱长都相等，‎ 故存在唯一平面.使平面且截此正方体所得截面为正六边形，‎ 则③正确；‎ 对④：若棱在平面的同侧，则为过点且与平面平行的平面；‎ 若棱中有一条棱与另外两条棱分别在平面的异侧，则这样的平面有3个；‎ 故满足题意的平面有4个.‎ 故④错误.‎ 综上所述：正确的有①②③.‎ 故答案为：①②③.‎ ‎【点睛】本题考查线面角的求解，以及棱锥体积的计算，正方体截面的相关性质，属综合中档题.‎ 三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.‎ ‎17.如图，在四棱锥中，平面，是正方形，是中点，点在上，且.‎ ‎（1）证明：平面；‎ ‎（2）若，求点到平面的距离.‎ ‎【答案】(1)证明见详解；(2).‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据平面，可得，再证，即可由线线垂直推证线面垂直；‎ ‎（2）转换三棱锥顶点，用等体积法求点面距离即可.‎ ‎【详解】‎ ‎（1）因为平面，平面，故可得；‎ 设底面正方形的边长为4，故可得，‎ ‎，，‎ 故在中，满足，故可得；‎ 又平面，且，‎ 则平面，即证.‎ ‎（2）因为平面，故为三棱锥底面上的高线.‎ 故可得.‎ 在中，因为，，‎ 由（1）可知平面，又平面，故可得，‎ 则，‎ 设点到平面的距离为，‎ 故可得，解得.‎ 即点到平面的距离为：.‎ ‎【点睛】本题考查由线线垂直推证线面垂直，以及利用等体积法求解点到面的距离，属综合基础题.‎ ‎18.已知的面积为3，边上的高是2，.‎ ‎（1）求外接圆的半径；‎ ‎（2）求和的长.‎ ‎【答案】(1)；(2)或 ‎【解析】‎ ‎【分析】‎ ‎（1）利用三角形的面积公式求得，再利用同角三角函数关系，求得，最后利用正弦定理，即可求得外接圆半径；‎ ‎（2）利用面积公式以及余弦定理，求得和的方程组，解方程组即可.‎ ‎【详解】设三角形的边长.‎ ‎（1）由面积公式，解得.‎ 因为，，故由同角三角函数关系，‎ 容易得.‎ 由正弦定理可得.‎ 故外接圆的半径为.‎ ‎（2）由面积公式可得，结合（1）中所求，‎ 可得；‎ 由余弦定理可得，解得，‎ 即 解得，联立 可得或.‎ 故或.‎ ‎【点睛】本题考查利用正弦定理和余弦定理解三角形，以及三角形外接圆半径的求解，属综合基础题.‎ ‎19.在统计调查中，问卷的设计是一门很大的学问，特别是对一些敏感性问题.例如学生在考试中有无作弊现象，社会上的偷税漏税等，更要精心设计问卷.设法消除被调查者的顾虑，使他们能够如实回答问题，否则被调查者往往会拒绝回答，或不提供真实情况.为了调查中学生中的早恋现象，随机抽出200名学生，调查中使用了两个问题.①你的血型是A型或B型(资料：我国人口型血比例41%，型血比例28%，型血比例24%.型血比例7% ).②你是否有早恋现象，让被调查者掷两枚骰子，点数之和为奇数的学生如实回答第一个问题.点数之和为偶数的学生如实回答第二个问题，回答“是”的人往一个盒子中放一个小石子，回答“否”的人什么都不放，后来在盒子中收到了57个小石子.‎ ‎（1）试计算掷两枚骰子点数之和为偶数的机率；‎ ‎（2）你能否估算出中学生早恋人数的百分比？‎ ‎【答案】(1)；(2).‎ ‎【解析】‎ ‎【分析】‎ ‎（1）先计算抛掷两枚骰子的所有可能，再找出满足题意的可能，用古典概型的概率计算公式即可求得；‎ ‎（2）根据（1）中所求，结合参考数据，先求得关于血型问题回答是的同学数量，再求出回答是早恋同学的数量，进而算出早恋比例.‎ ‎【详解】（1）抛掷两枚骰子，总共有36种可能；‎ 其中满足点数之和为偶数有以下18中可能：‎ 故满足题意的概率.‎ 故掷两枚骰子点数之和为偶数的机率为.‎ ‎（2）由（1）可知，点数之和为偶函数和奇数的概率相等，‎ 则可估算有100名同学回答第一个问题，100名同学回答第二个问题.‎ 根据参考数据，回答第一个问题，选择是的有人；‎ 故回答第二个问题，选择是的有人.‎ 故早恋人数的占比为.‎ ‎【点睛】本题考查简单随机抽样的概率计算，属基础题.‎ ‎20.已知函数（）‎ ‎（1）当时，求曲线在点处的切线方程；‎ ‎（2）若在定义域内为单调函数，求实数的取值范围.‎ ‎【答案】(1)；(2).‎ ‎【解析】‎ ‎【分析】‎ ‎（1）对函数求导，解得函数在点处切线的斜率，根据点斜式即可求得切线方程；‎ ‎（2）构造函数，利用导数求解其值域，再根据与之间的关系，求解恒成立问题即可得参数的范围.‎ ‎【详解】（1）当时，，故；‎ 故可得，‎ 故切线方程为：，整理得.‎ 故曲线在点处的切线方程为.‎ ‎（2）因为，故可得.‎ 若在定义域内为单调函数，则恒成立，或恒成立.‎ 构造函数，故可得，‎ 令，解得，‎ 故在区间上单调递增，在区间上单调递减.‎ 故，且当趋近于0时，趋近于0.‎ 故.‎ 若要保证在定义域内恒成立，即恒成立，‎ 即在定义域内恒成立，则只需；‎ 若要保证在定义域内恒成立，则恒成立，‎ 则在定义域内恒成立，但没有最小值，故舍去.‎ 综上所述，要保证在定义域内为单调函数，‎ 则.‎ ‎【点睛】本题考查导数的几何意义，以及根据函数单调性，利用导数求参数的范围，属综合中档题.‎ 选考题：共10分，请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题计分，作答时用2B铅笔在答题卡上把所选题目的题号涂黑.‎ ‎21.已知椭圆：（）的左焦点为，其中四个顶点围成的四边形面积为.‎ ‎（1）求椭圆的标准方程；‎ ‎（2）过点的直线与曲线交于，两点，设的中点为，，两点为椭圆上关于原点对称的两点，且（），求四边形面积的最小值.‎ ‎【答案】(1)；(2)4‎ ‎【解析】‎ ‎【分析】‎ ‎（1）将四边形面积表示为的代数式，结合焦点坐标，联立方程组，求解即可；‎ ‎（2）设出直线的方程，利用弦长公式求得，再利用，建立直线与之间的联系，再利用点到直线的距离，以及面积公式，将四边形面积表示为函数形式，求该函数的最小值即可.‎ ‎【详解】（1）因为左焦点为，故可得；‎ 因为四个顶点围成四边形面积为，故可得.‎ 联立，‎ 解得 故椭圆方程为.‎ ‎（2）因为，故两点不可能重合，‎ 则直线的斜率不可能为0，‎ 故可设直线方程为，‎ 联立椭圆方程，‎ 可得，‎ 设两点坐标分别为，‎ 则可得，‎ 则 故可得，‎ 因为，故可得四点共线，‎ 故可得.‎ 不妨设直线方程为，，‎ 联立直线与椭圆方程 可得，‎ 设，‎ 则，即 则，即 则点到直线的距离为：‎ 将代入上式即可得：‎ ‎，，‎ 故 又根据弦长公式可得：‎ 故四边形面积 ‎，‎ 因为，故可得，‎ 当且仅当时，四边形面积取得最小值4.‎ 故四边形面积的最小值为.‎ ‎【点睛】本题考查椭圆方程的求解，以及椭圆中四边形面积的最值，涉及弦长公式的应用，计算量相对较大，属中档题.‎ ‎22.在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，四边形的四个顶点都在曲线上.‎ ‎（1）求曲线的直角坐标方程；‎ ‎（2）若，相交于点，求的值.‎ ‎【答案】(1)；(2)4‎ ‎【解析】‎ ‎【分析】‎ ‎（1）将两边平方，利用公式，即可转化为直角坐标方程；‎ ‎（2）写出直线的参数方程，根据直线参数的几何意义，即可求得.‎ ‎【详解】（1）将两边平方，即可得，‎ 即可得.‎ ‎（2）因为直线都经过点，‎ 故直线的参数方程为：为参数；‎ 直线的参数方程为：为参数；‎ 联立直线的方程与可得：‎ ‎，‎ 设两点对应的参数为，故可得；‎ 同理联立直线的方程与可得：‎ ‎，‎ 设两点对应的参数为，故可得；‎ 根据直线参数方程中几何意义可知：‎ ‎.即为所求.‎ ‎【点睛】本题考查极坐标方程转化为直角坐标方程，以及利用直线参数方程中参数的几何意义，求解线段长度的乘积，属基础题.‎ ‎23.已知函数.‎ ‎（1）求不等式的解集；‎ ‎（2）若不等式的解集包含，求实数的取值范围.‎ ‎【答案】(1)；(2).‎ ‎【解析】‎ ‎【分析】‎ ‎（1）分类讨论，求解不等式即可；‎ ‎（2）将问题转化为二次函数在区间上恒成立的问题，列出不等式组即可求得.‎ ‎【详解】（1）当时，等价于，‎ 解得；‎ 当时，等价于，恒成立，‎ 解得；‎ 当时，等价于，‎ 解得；‎ 综上所述，不等式的解集为.‎ ‎（2）不等式的解集包含，‎ 等价于在区间上恒成立，‎ 也等价于在区间恒成立.‎ 则只需满足：‎ 且即可.‎ 即，‎ 解得.‎ ‎【点睛】本题考查绝对值不等式的求解，以及二次函数在区间上恒成立的问题，属综合基础题.‎