专题2-12 概率与统计相结合问题（测）-2017年高考数学（理）二轮复习讲练测 Word版含解析 17页

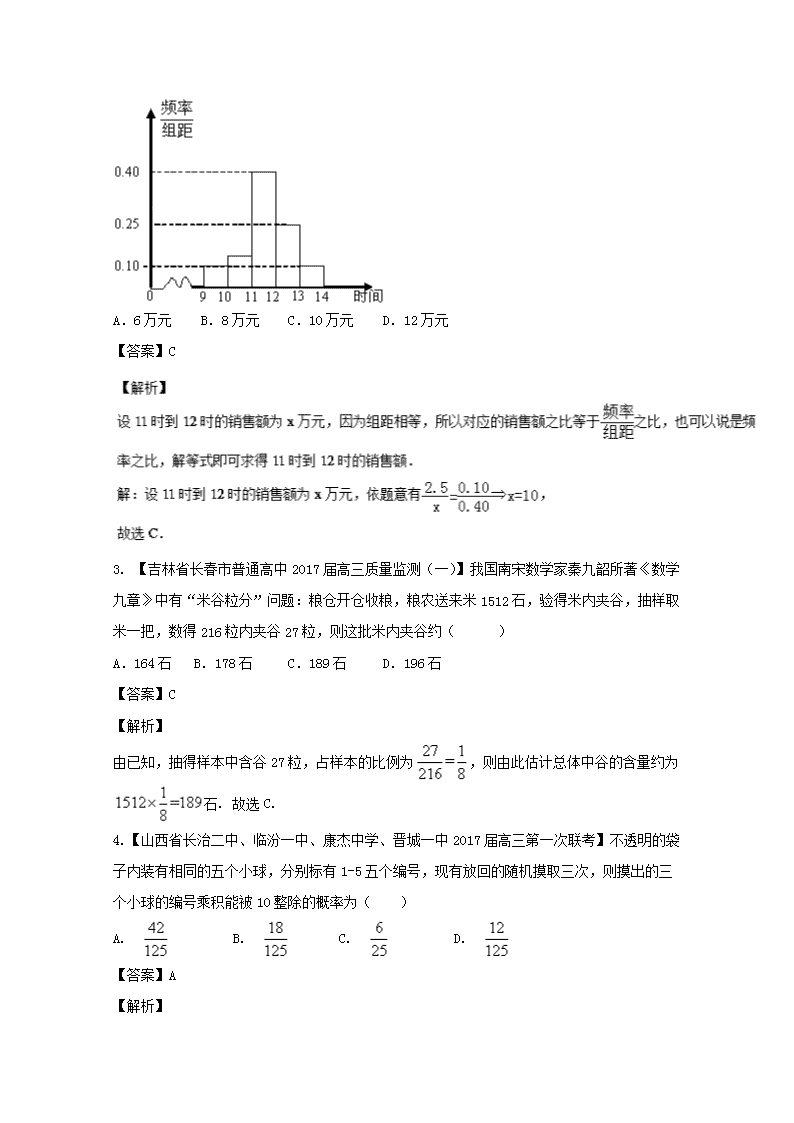
www.ks5u.com 总分 150分 时间 120分钟 班级 _______ 学号 _______ 得分_______‎ （一） 选择题（12*5=60分）‎ ‎1【山西省孝义市2017届高三上学期二轮模考】已知，，则函数的图象恒在轴上方的概率为（ ）‎ A． B． C. D．‎ ‎【答案】D ‎2.【2016届湖南师大附中高三上学期第四次】某商场在国庆黄金周的促销活动中，对10月2日9时到14时的销售额进行统计，其频率分布直方图如图所示，已知9时至10时的销售额为2.5万元，则11时到12时的销售额为（ ）‎ A．6万元 B．8万元 C．10万元 D．12万元 ‎【答案】C ‎3. 【吉林省长春市普通高中2017届高三质量监测（一）】我国南宋数学家秦九韶所著《数学九章》中有“米谷粒分”问题：粮仓开仓收粮，粮农送来米1512石，验得米内夹谷，抽样取米一把，数得216粒内夹谷27粒，则这批米内夹谷约（ ）‎ A．164石 B．178石 C．189石 D．196石 ‎【答案】C ‎【解析】‎ 由已知，抽得样本中含谷27粒，占样本的比例为，则由此估计总体中谷的含量约为石. 故选C.‎ ‎4.【山西省长治二中、临汾一中、康杰中学、晋城一中2017届高三第一次联考】不透明的袋子内装有相同的五个小球，分别标有1-5五个编号，现有放回的随机摸取三次，则摸出的三个小球的编号乘积能被10整除的概率为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ 由题意5号，2号或4号至少摸出一次，即三种情况：一是5号摸出两次，2号或4号摸出一次；二是5号摸出一次，2号或4号摸出两次；三是5号摸出一次，2号或4号摸出一次，1号或3号摸出一次；，总共有，所求概率为，选A.‎ ‎5.【湖南省长沙市长郡中学2017届高三摸底】一个不透明的袋子装有4个完全相同的小球，球上分别标有数字为0,1,2,2，现甲从中摸出一个球后便放回，乙再从中摸出一个球，若摸出的球上数字大即获胜（若数字相同则为平局），则在甲获胜的条件下，乙摸1号球的概率为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ 甲摸的球数字在前，乙摸的球数字在后，则甲胜的情况有10，20，21，20，21共5种，其中乙摸1号球的有2种，因此概率为．‎ ‎6.为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为，众数为，平均值为，则(　　)‎ A．　　　 B． C． D．‎ ‎【答案】‎ ‎7.【广东省惠州市2017届第二次调研考试】已知随机变量服从正态分布，若，则（ ）‎ ‎（A） （B） （C） （D）‎ ‎【答案】C ‎【解析】‎ 因为已知随机变量服从正态分布，所以正态曲线关于直线对称，又，所以，‎ ‎，故选C．‎ ‎8.根据如下样本数据 ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎4.0‎ ‎2.5‎ ‎0.5‎ 得到的回归方程为，则（ ）‎ A. , B. , C. , D. , ‎ ‎【答案】B ‎【解析】‎ 依题意，画散点图知，两个变量负相关，所以，.选B.‎ ‎9.【广东省珠海市2017届高三9月摸底】一个路口的红绿灯，红灯的时间为秒，黄灯的时间为秒，绿灯的时间为秒，当你到达路口时，不需要等待就可以过马路的概率为 ‎ A. 　　 B. C. D. ‎ ‎【答案】. ‎ ‎10.【四川省成都市2017届高中毕业班摸底】某班50名学生中有女生20名，按男女比例用分层抽样的方法，从全班学生中抽取部分学生进行调查，已知抽到的女生有4名，则本次调查抽取的人数是（ ）‎ A．8 B．10 C．12 ‎ ‎ D．15‎ ‎【答案】B ‎【解析】‎ 因为名学生中有女生名，按男女比例用分层抽样的方法，抽到的女生有名，所以本次调查抽取的人数是，故选B.‎ ‎11.【广东省惠州市2017届高三第一次调研】某产品的广告费用与销售额的统计数据如下表：‎ 广告费用（万元）‎ ‎1‎ ‎2‎ ‎4‎ ‎5‎ 销售额（万元）‎ ‎10‎ ‎26‎ ‎35‎ ‎49‎ 根据上表可得回归方程的约等于9，据 此模型预报广告费用为6万元时，销售额约为（ ）。‎ A．54万元 B．55万元 C．56万元 D．57万元 ‎【答案】D ‎12.【湖北省襄阳市第四中学2017届高三七月第二周周考】已知甲、乙两组数据如茎叶图所示，若它们的中位数相同，平均数也相同，则图中的m,n的比 值＝（ ）‎ A．1 B． C． D．‎ ‎【答案】D ‎【解析】‎ 由茎叶图可知乙的中位数是，甲、乙两组数据中位数相同所以，所以甲的平均数为，甲、乙两组数据平均数也相同，所以，解得，所以．‎ 二、填空题（4*5=20分）‎ ‎13.【广西梧州市2017届高三上学期摸底联考】在上随机取一个实数，能使函数在上有零点的概率为___________．‎ ‎【答案】‎ ‎【解析】‎ 若有零点，则，解得或，则函数有零点的概率，故答案为．‎ ‎14.【2016届山东枣庄八中高三2月月考理科】某高校为了了解教研工作开展状况与教师年龄之间的关系，将该校不小于35岁的80名教师按年龄分组，分组区间为，，，，，由此得到频率分布直方图如图，则这80名教师中年龄小于45岁的教师有________人．‎ ‎【答案】48‎ ‎15.‎ ‎【浙江省温州市普通高中2017届高三8月模拟】盒中有大小相同的5个白球和3个黑球，从中随机摸出3个小球，记摸到黑球的个数为，则_________，__________．　‎ ‎【答案】‎ ‎【解析】‎ ‎，，，，所以．‎ ‎16.【江苏省苏州市2017届高三暑假自主学习测试】已知等差数列的公差为d，若的方差为8, 则d的值为 ．‎ ‎【答案】2‎ 三．解答题 ‎17.【四川省成都市新都一中2016届高三月考】某校为进行爱国主义教育，在全校组织了一次有关钓鱼岛历史知识的竞赛．现有甲、乙两队参加钓鱼岛知识竞赛，每队3人，规定每人回答一个问题，答对为本队赢得1分，答错得0分．假设甲队中每人答对的概率均为，乙队中3人答对的概率分别为、、，且各人回答正确与否相互之间没有影响，用ξ表示甲队的总得分．‎ ‎(Ⅰ) 求随机变量ξ的分布列和数学期望；‎ ‎(Ⅱ) 用A表示“甲、乙两个队总得分之和等于3”这一事件，用B表示“甲队总得分大于乙队总得分” 这一事件，求P(AB)．‎ ‎【答案】(1)2；(2)‎ ‎【解析】试题分析：(1)甲队的得分分布服从二项分布：～(3，)；(2)事件AB等价于“甲得2分乙得1分”或“甲得3分乙得0分”，据此可以求出P(AB).‎ 试题解析：(Ⅰ)解法一：由题意知，的可能取值为0，1，2，3，且 ‎，，‎ ‎，．‎ 所以的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ 的数学期望为．‎ ‎18. 【广东省惠州市2017届高三第一次调研】4月23日是世界读书日，惠州市某中学在此期间开展了一系列的读书教育活动。为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位：分钟)的频率分布直方图，且将日均课外阅读时间不低于60分钟的学生称为“读书迷”，低于60分钟的学生称为“非读书迷”．‎ ‎（Ⅰ）根据已知条件完成下面2×2列联表，并据此判断是否有99%的把握认为“读书迷”与性别有关？‎ 非读书迷 读书迷 合计 男 ‎15‎ 女 ‎45‎ 合计 ‎ ‎ ‎（Ⅱ）将频率视为概率，现在从该校大量学生中用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中“读书迷”的人数为，若每次抽取的结果是相互独立的，求的分布列、数学期望和方差．‎ 附：‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.001‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎10.828‎ ‎【答案】（Ⅰ）有99%的把握认为“读书迷”与性别有关． ‎ ‎（Ⅱ）的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎，‎ ‎.‎ ‎【解析】（Ⅰ）2×2列联表如下：‎ 非读书迷 读书迷 合计 男 ‎40‎ ‎15‎ ‎55‎ 女 ‎20‎ ‎25‎ ‎45‎ 合计 ‎60‎ ‎40‎ ‎100‎ 易知的观测值....................4分 因为8.249>6.635，所以有99%的把握认为“读书迷”与性别有关．..............5分 ‎19. 【吉林省长春市普通高中2017届高三质量监测（一）】某人种植一种经济作物，根据以往的年产量数据，得到年产量频率分布直方图如图所示，以各区间中点值作为该区间的年产量，得到平均年产量为455，已知当年产量低于350时，单位售价为20元/，若当年产量不低于350而低于550时，单位售价为15元/，当年产量不低于550时，单位售价为10元/.‎ ‎（1）求图中的值；‎ ‎（2）试估计年销售额的期望是多少？‎ ‎【答案】（1）（2）6525‎ ‎20.【2016高考天津理数】某小组共10人，利用假期参加义工活动，已知参加义工活动次数为1,2,3的人数分别为3,3,4,.现从这10人中随机选出2人作为该组代表参加座谈会.‎ ‎（I）设A为事件“选出的2人参加义工活动次数之和为4”，求事件A发生的概率；‎ ‎（II）设为选出的2人参加义工活动次数之差的绝对值，求随机变量的分布列和数学期望. ‎ ‎【答案】（Ⅰ）（Ⅱ）详见解析 ‎【解析】‎ 由已知，有 所以，事件发生的概率为.‎ 随机变量的所有可能取值为 ‎，‎ ‎，‎ ‎.‎ 所以，随机变量分布列为 随机变量的数学期望.‎ ‎21.【2016高考山东理数】甲、乙两人组成“星队”参加猜成语活动，每轮活动由甲、乙各猜一个成语，在一轮活动中，如果两人都猜对，则“星队”得3分；如果只有一个人猜对，则“星队”得1分；如果两人都没猜对，则“星队”得0分.已知甲每轮猜对的概率是，乙每轮猜对的概率是；每轮活动中甲、乙猜对与否互不影响，各轮结果亦互不影响.假设“星队”参加两轮活动，求：‎ ‎（I）“星队”至少猜对3个成语的概率；‎ ‎（Ⅱ）“星队”两轮得分之和为X的分布列和数学期望EX.‎ ‎【答案】（Ⅰ）（Ⅱ）分布列见解析，‎ ‎22.【2016年高考四川理数】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨）、一位居民的月用水量不超过的部分按平价收费，超出的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5)，[0.5,1)，…，[4,4.5)分成9组，制成了如图所示的频率分布直方图.‎ ‎（I）求直方图中a的值；‎ ‎（II）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；‎ ‎（III）若该市政府希望使85%的居民每月的用水量不超过标准（吨），估计的值，并说明理由.‎ ‎【答案】（Ⅰ）；（Ⅱ）36000；（Ⅲ）2.9．‎ ‎ ‎