2021版新高考数学一轮复习单元质检卷九统计与统计案例新人教A版 14页

1 单元质检卷九　统计与统计案例 (时间:45 分钟　满分:100 分) 一、选择题(本大题共 6 小题,每小题 7 分,共 42 分) 1.(2019 湖北鄂州模拟,5)采用系统抽样方法从 960 人中抽取 32 人做问卷调查,为此将他们随机编 号 1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为 29,则抽到的 32 人中,编号 落入区间[200,480]的人数为 (　　) A.7 B.9 C.10 D.12 2.(2019 江西赣州模拟,4)某学校高一年级 1 802 人,高二年级 1 600 人,高三年级 1 499 人,先采用 分层抽样的方法从中抽取 98 名学生参加全国中学生禁毒知识竞赛,则在高一、高二、高三三个年 级中抽取的人数分别为(　　) A.35,33,30 B.36,32,30 C.36,33,29 D.35,32,31 3.若样本 1+x1,1+x2,1+x3,…,1+xn 的平均数是 10,方差为 2,则对于样本 2+2x1,2+2x2,2+2x3,…,2+2xn,下列结论正确的是(　　) A.平均数为 20,方差为 4 B.平均数为 11,方差为 4 C.平均数为 21,方差为 8 D.平均数为 20,方差为 8 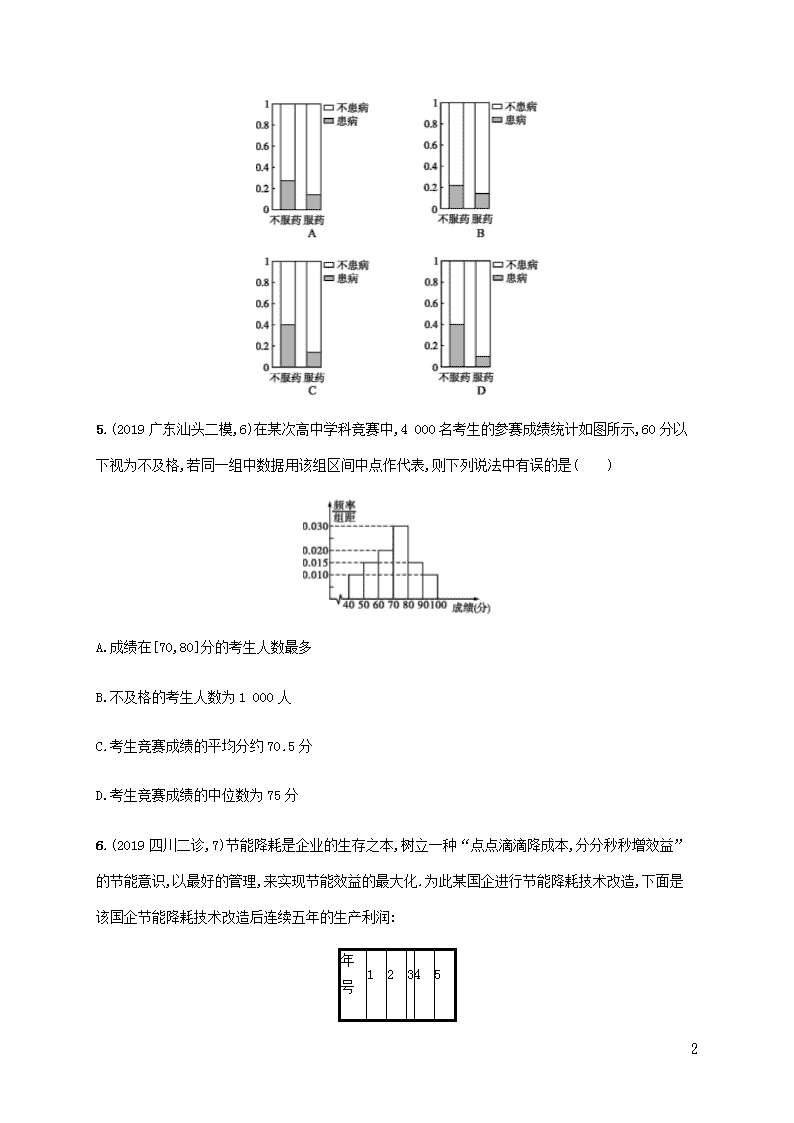4.为考察某种药物对预防禽流感的效果,在四个不同的实验室取相同的个体进行动物试验,根据四 个实验室得到的列联表画出如下四个等高条形图,最能体现该药物对预防禽流感有效果的图形是 (　　) 2 5.(2019 广东汕头二模,6)在某次高中学科竞赛中,4 000 名考生的参赛成绩统计如图所示,60 分以 下视为不及格,若同一组中数据用该组区间中点作代表,则下列说法中有误的是(　　) A.成绩在[70,80]分的考生人数最多 B.不及格的考生人数为 1 000 人 C.考生竞赛成绩的平均分约 70.5 分 D.考生竞赛成绩的中位数为 75 分 6.(2019 四川二诊,7)节能降耗是企业的生存之本,树立一种“点点滴滴降成本,分分秒秒增效益” 的节能意识,以最好的管理,来实现节能效益的最大化.为此某国企进行节能降耗技术改造,下面是 该国企节能降耗技术改造后连续五年的生产利润: 年 号 1 2 34 5 3 年 生 产 利 润 y( 单 位: 千 万 元) 0. 7 0. 8 1 1. 1 1. 4 预测第 8 年该国企的生产利润约为(　　)千万元 参考公式及数据: ^ b = n ∑ i = 1 (xi - x)(yi - y) n ∑ i = 1 (xi - x)2 = n ∑ i = 1 xiyi - nxy n ∑ i = 1 x2i - nx2 ; ^ a = y - ^ bx, 5 ∑ i = 1 (xi-x)(yi-y)=1.7, 5 ∑ i = 1 x2i-n x2=10 A.1.88 B.2.21 C.1.85 D.2.34 二、填空题(本大题共 3 小题,每小题 7 分,共 21 分) 7.某公司对一批产品的质量进行检测,现采用系统抽样的方法从 100 件产品中抽取 5 件进行检测, 对这 100 件产品随机编号后分成 5 组,第一组 1~20 号,第二组 21~40 号,…,第五组 81~100 号,若在 第二组中抽取的编号为 24,则在第四组中抽取的编号为　　　　　. 8.(2019 安徽六安毛坦厂中学联考,14)我国古代数学算经十书之一的《九章算术》有一衰分问题: 今有北乡八千一百人,西乡九千人,南乡五千四百人,凡三乡,发役五百,意思是用分层抽样的方法从 这三个乡中抽出 500 人服役,则北乡比南乡多抽　　　　人. 4 9.某单位为了了解用电量 y(度)与气温 x(℃)之间的关系,随机统计了某 4 天的用电量与当天气温, 并制作了如下面的对照表.由表中数据,得回归直线方程 ^ y = ^ bx+ ^ a,若 ^ b=-2,则 ^ a=　　　　　. 气温 x(℃) 181310-1 用电量 y(度) 24343864 三、解答题(本大题共 3 小题,共 37 分) 10.(12 分)(2019 湖北仙桃中学模拟,19)“共享单车”的出现,为我们提供了一种新型的交通方式. 某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的 A 城市和交通拥堵严重的 B 城 市分别随机调查了 20 个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图: (1)根据茎叶图,比较两城市满意度评分的平均值的大小及方差的大小(不要求计算具体值,给出结 论即可); (2)若得分不低于 80 分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式 “不认可”,请根据此样本完成此列联表,并据此样本分析是否有 95%的把握认为城市拥堵与认可共 享单车有关; (3)若此样本中的 A 城市和 B 城市各抽取 1 人,则在此 2 人中恰有一人认可的条件下,此人来自 B 城 市的概率是多少? 5 AB 合 计 认可 不认 可 合计 附:K2= n(ad - bc)2 (a + b)(c + d)(a + c)(b + d) P(K2≥k0 ) 0.0500.0100.001 k0 3.8416.635 10.82 8 11.(12 分)(2019 福建三明模拟,19)近年来,随着我国汽车消费水平的提高,二手车行业得到迅猛发 展,某汽车交易市场对 2019 年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计, 得到频率分布直方图如图 1. 6 图 1 图 2 (1)记“在 2019 年成交的二手车中随机选取一辆,该车的使用年限在(8,16]”为事件 A,试估计 A 的 概率; (2)根据该汽车交易市场的历史资料,得到散点图如图 2,其中 x(单位:年)表示二手车的使用时 间,y(单位:万元)表示相应的二手车的平均交易价格. 由散点图看出,可采用 y=ea+bx 作为二手车平均交易价格 y 关于其使用年限 x 的回归方程,相关数据 如下表 表中 Yi=ln yi,Y = 1 10 10 ∑ i = 1 Yi ; x y Y 10 ∑ i = 1 xiyi 10 ∑ i = 1 xiYi 10 ∑ i = 1 x2i 5. 5 8.71.9301.479.75385 7 ①根据回归方程类型及表中数据,建立 y 关于 x 的回归方程; ②该汽车交易市场对使用 8 年以内(含 8 年)的二手车收取成交价格 4%的佣金,对使用时间 8 年以上 (不含 8 年)的二手车收取成交价格 10%的佣金.在图 1 对使用时间的分组中,以各组的区间中点值代 表该组的各个值.若以 2019 年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平 均佣金. 附注:①对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线 v=α+βu 的斜率和截距的最小二乘 估计分别为 ^ β = n ∑ i = 1 uivi - nuv n ∑ i = 1 u2i - nu2 , ^ α = v - ^ βu. ②参考数据:e2.95≈19.1,e1.75≈5.75,e0.35≈1.73,e-0.65≈0.52,e-1.85≈0.16. 12.(13 分)某高中有高一新生 500 名,分成水平相同的 A,B 两类教学实验,为对比教学效果,现用分 层抽样的方法从 A,B 两类学生中分别抽取了 40 人,60 人进行测试. (1)求该学校高一新生 A,B 两类学生各多少人? (2)经过测试,得到以下三个数据图表: 75 分以上 A,B 两类参加测试学生成绩的茎叶图 8 图 1 100 名测试学生成绩的频率分布直方图 图 2 100 名学生成绩频率分布表: 组 号 分组 频 数 频 率 1 [55,60 ) 5 0.0 5 2 [60,65 ) 20 0.2 0 3 [65,70 ) 4 [70,75 ) 35 0.3 5 5 [75,80 ) 6 [80,85 ) 合计 10 0 1.0 0 9 ①先填写频率分布表中的六个空格,然后将频率分布直方图(图 2)补充完整; ②该学校拟定从参加考试的 79 分以上(含 79 分)的 B 类学生中随机抽取 2 人代表学校参加市比赛, 求抽到的 2 人分数都在 80 分以上的概率. 参考答案 单元质检卷九　统计与统计案例 1.C　每组人数为 960÷32=30 人,即抽到号码数的间隔为 30,因为第一组抽到的号码为 29,根据系 统抽样的定义,抽到的号码数可组成一个等差数列,且 an=29+30(n-1)=30n-1,n∈N*,令 200≤30n- 1≤480,得201 30 ≤ n ≤ 481 30 ,可得 n 的取值可以从 7 取到 16,共 10 个,故选 C. 2.B　先将每个年级的人数取整,得高一 1800 人,高二 1600 人,高三 1500 人,∴三个年级的总人数 所占比例分别为18 49,16 49,15 49,因此,各年级抽取人数分别为 98 × 18 49=36,98 × 16 49=32,98 × 15 49=30,故选 B. 3.D　样本 1+x1,1+x2,1+x3,…,1+xn 的平均数是 10,方差为 2,则数据 x1,x2,x3,…,xn 的平均数是 9, 方差是 2; 所以样本 2+2x1,2+2x2,2+2x3,…,2+2xn 的平均数是 2+2×9=20,方差为 22×2=8. 10 4.D　根据四个列联表的等高条形图知,图形 D 中不服药与服药时患禽流感的差异最大,它最能体现 该药物对预防禽流感有效果.故选 D. 5.D　A 选项,由频率分布直方图可得,成绩在[70,80]的频率最高,因此考生人数最多,故 A 正确;B 选项,由频率分布直方图可得,成绩在[40,60)的频率为 0.25,因此,不及格的人数为 4000×0.25=1000,即 B 正确;C 选项,由频率分布直方图可得: 平均分等于 45×0.1+55×0.15+65×0.2+75×0.3+85×0.15+95×0.1=70.5,即 C 正确; D 选项,因为成绩在[40,70)的频率为 0.45,由[70,80]的频率为 0.3,所以中位数为 70+10 × 0.05 0.3 ≈ 71.67,故 D 错误.故选 D. 6.C　由题可得:x = 1 + 2 + 3 + 4 + 5 5 =3,y = 0.7 + 0.8 + 1 + 1.1 + 1.4 5 =1,所以 ^ b = 1.7 10 =0.17,又 ^ a = y - ^ b x=1-0.17×3=0.49,所以利润与年号的回归方程为 ^ y=0.17x+0.49,当 x=8 时, ^ y=0.17×8+0.49=1.85, 故选 C. 7.64　设在第一组中抽取的号码为 a1,则在各组中抽取的号码构成首项为 a1,公差为 20 的等差数列, 即 an=a1+(n-1)×20,又在第二组中抽取的号码为 24,即 a1+20=24,所以 a1=4,所以在第四组中抽取的 号码为 4+(4-1)×20=64. 8.60　由题意可得,三乡共有 8100+9000+5400=22500 人,从中抽取 500 人,因此抽样比为 500 22500 = 1 45, 所以北乡共抽取 8100 × 1 45=180 人;南乡共抽取 5400 × 1 45=120 人,所以北乡比南乡多抽 180- 120=60 人.故答案为 60. 9.60　由表中数据,计算x = 1 4 × (18+13+10-1)=10, y = 1 4 × (24+34+38+64)=40, 代入回归直线方程 ^ y = ^ bx+ ^ a中,得 40=-2×10+ ^ a,解得 ^ a=60. 11 10.解(1)A 城市评分的平均值小于 B 城市评分的平均值; A 城市评分的方差大于 B 城市评分的方差. (2) A B 合 计 认 可 5 1015 不 认 可 151025 合 计 202040 K2=40 × (5 × 10 - 10 × 15)2 20 × 20 × 15 × 25 ≈ 2.667<3.841,所以没有 95%的把握认为城市拥堵与认可共享单车 有关. (3)设事件 M:恰有一人认可; 事件 N:来自 B 城市的人认可; 事件 M 包含的基本事件数为 5×10+10×15=200, 事件 M∩N 包含的基本事件数为 10×15=150,则所求的条件概率 P(N|M)=P(N⋂M) P(M) = 150 200 = 3 4. 11.解(1)由频率分布直方图得,该汽车交易市场 2019 年成交的二手车使用时间在(8,12]的频率为 0.07×4=0.28,在(12,16]的频率为 0.02×4=0.12, 所以 P(A)=0.28+0.12=0.40. 12 (2)①由 y=ea+bx 得 lny=a+bx,即 Y 关于 x 的线性回归方程为 ^ Y=a+bx, 因为 ^ b = 10 ∑ i = 1 xiYi - 10x·Y 10 ∑ i = 1 x2i - 10x2 = 79.75 - 10 × 5.5 × 1.9 385 - 10 × 5.52 =-0.3, ^ a = Y - ^ bx=1.9-(-0.3)×5.5=3.55,所以 Y 关于 x 的线性回归方程为 ^ Y=3.55-0.3x,即 y 关于 x 的回归方程为 ^ y=e3.55-0.3x. ②根据①中的回归方程 ^ y=e3.55-0.3x 和题图 1,对成交的二手车可预测; 使用时间在(0,4]的平均成交价格为 e3.55-0.3×2=e2.95≈19.1,对应的频率为 0.2; 使用时间在(4,8]的平均成交价格为 e3.55-0.3×6=e1.75≈5.75,对应的频率为 0.36; 使用时间在(8,12]的平均成交价格为 e3.55-0.3×10=e0.55≈1.73,对应的频率为 0.28; 使用时间在(12,16]的平均成交价格为 e3.55-0.3×14=e-0.65≈0.52,对应的频率为 0.12; 使用时间在(16,20]的平均成交价格为 e3.55-0.3×18=e-1.85≈0.16,对应的频率为 0.04; 所以该汽车交易市场对于成交的每辆车可获得的平均佣金为 (0.2×19.1+0.36×5.75)×4%+(0.28×1.73+0.12×0.52+0.04×0.16)×10%=0.290 92≈0.29 万元. 12.解(1)由题意知 A 类学生有 500 × 40 40 + 60=200(人), 则 B 类学生有 500-200=300(人). (2)① 组分组 频 频 13 号 数 率 1 [55,60 ) 5 0.0 5 2 [60,65 ) 20 0.2 0 3 [65,70 ) 25 0.2 5 4 [70,75 ) 35 0.3 5 5 [75,80 ) 10 0.1 0 6 [80,85 ) 5 0.0 5 合计 10 0 1.0 0 ②79 分以上的 B 类学生共 4 人,记 80 分以上的三人分别是{1,2,3},79 分的学生为{a}.从中抽 取 2 人,有(12)、(13)、(1a)、(23)、(2a)、(3a)共 6 种抽法,抽出 2 人均在 80 分以上有(12)、 (13)、(23)共 3 种抽法,则抽到 2 人均在 80 分以上的概率为 P=3 6 = 1 2. 1