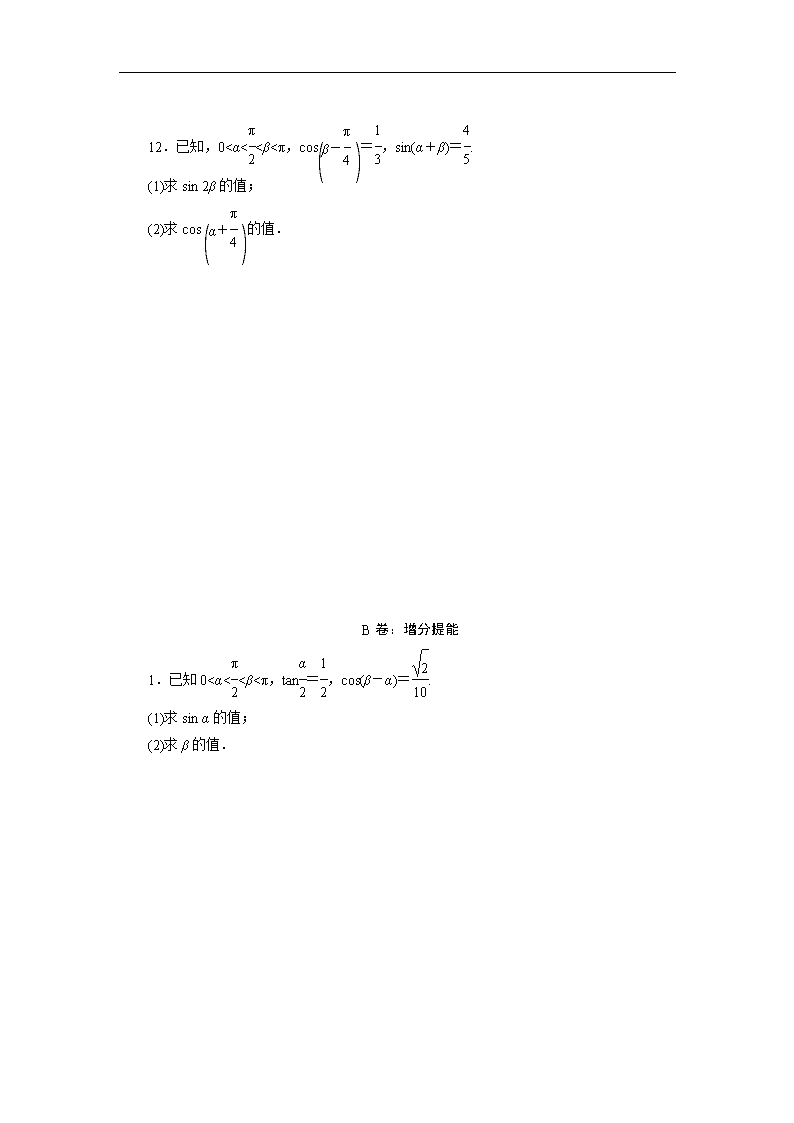2016届高考数学（理）大一轮复习达标训练试题：课时跟踪检测(二十三)　简单的三角恒等变换 9页

课时跟踪检测(二十三)　简单的三角恒等变换 ‎(分A、B卷，共2页)‎ A卷：夯基保分 一、选择题 ‎1．(2015·洛阳统考)已知sin 2α＝，则cos2＝(　　)‎ A．－　　　　　　　　　 B．－ C. D. ‎2．(2015·青岛二模)设tan＝，则tan＝(　　)‎ A．－2 B．2‎ C．－4 D．4‎ ‎3．已知角α的顶点与原点O重合，始边与x轴的正半轴重合，若它的终边经过点P(2,3)，则tan＝(　　)‎ A．－ B. C. D．－ ‎4．若α∈，且3cos 2α＝sin，则sin 2α的值为(　　)‎ A. B．－ C. D．－ ‎5．cos·cos·cos＝(　　)‎ A．－ B．－ C. D. ‎6．定义运算＝ad－bc.若cos α＝，＝，0<β<α<，则β等于(　　)‎ A. B. C. D. 二、填空题 ‎7．(2014·山东高考)函数y＝sin 2x＋cos2x的最小正周期为________．‎ ‎8．若锐角α、β满足(1＋tan α)(1＋tan β)＝4，则α＋β＝________.‎ ‎9.的值为________．‎ ‎10.＝________.‎ 三、解答题 ‎11．已知函数f(x)＝cos2x＋sin xcos x，x∈R.‎ ‎(1)求f的值；‎ ‎(2)若sin α＝，且α∈，求f.‎ ‎12．已知，0<α<<β<π，cos＝，sin(α＋β)＝.‎ ‎(1)求sin 2β的值；‎ ‎(2)求cos的值．‎ B卷：增分提能 ‎1．已知0<α<<β<π，tan＝，cos(β－α)＝.‎ ‎(1)求sin α的值；‎ ‎(2)求β的值．‎ ‎2．已知向量a＝(sin ωx，cos ωx)，b＝(cos φ，sin φ)，函数f(x)＝a·b的最小正周期为2π，其图象经过点M.‎ ‎(1)求函数f(x)的解析式；‎ ‎(2)已知α，β∈，且f(α)＝，f(β)＝，求f(2α－β)的值．‎ ‎3．已知角α的顶点在坐标原点，始边与x轴的正半轴重合，终边经过点P(－3，)．‎ ‎(1)求sin 2α－tan α的值；‎ ‎(2)若函数f(x)＝cos(x－α)cos α－sin(x－α)sin α，求函数g(x)＝f－‎2f2(x)在区间上的取值范围．‎ 答案 A卷：夯基保分 ‎1．选D　∵cos2＝＝，∴cos2＝.‎ ‎2．选C　因为tan＝＝，所以tan α＝，故tan＝＝－4.故选C.‎ ‎3．选D　依题意，角α的终边经过点P(2,3)，‎ 则tan α＝，tan 2α＝＝－，‎ 于是tan＝＝－.‎ ‎4．选D　cos 2α＝sin＝sin ‎＝2sincos 代入原式，得 ‎6sincos＝sin，‎ ‎∵α∈，∴cos＝，‎ ‎∴sin 2α＝cos ‎＝2cos2－1＝－.‎ ‎5．选A　cos·cos·cos ‎＝cos 20°·cos 40°·cos 100°‎ ‎＝－cos 20°·cos 40°·cos 80°‎ ‎＝－ ‎＝－ ‎＝－ ‎＝－＝－＝－.‎ ‎6．选D　依题意有 sin αcos β－cos αsin β＝sin(α－β)＝，‎ 又0<β<α<，∴0<α－β<，‎ 故cos(α－β)＝＝，‎ 而cos α＝，∴sin α＝，‎ 于是sin β＝sin[α－(α－β)]‎ ‎＝sin αcos(α－β)－cos αsin(α－β)‎ ‎＝×－×＝.‎ 故β＝.‎ ‎7．解析：y＝sin 2x＋cos 2x＋＝sin＋，所以其最小正周期为＝π.‎ 答案：π ‎8．解析：由(1＋tan α)(1＋tan β)＝4，‎ 可得＝，即tan(α＋β)＝.‎ 又α＋β∈(0，π)，所以α＋β＝.‎ 答案： ‎9．解析：原式＝ ‎＝ ‎＝＝＝＝1.‎ 答案：1‎ ‎10．解析：原式＝ ‎＝＝ ‎＝＝＝－4.‎ 答案：－4 ‎11．解：(1)f＝cos2＋sincos ＝2＋×＝.‎ ‎(2)因为f(x)＝cos2x＋sin xcos x＝＋sin 2x ‎＝＋(sin 2x＋cos 2x) ＝＋sin，‎ 所以f＝＋sin ‎＝＋sin ＝＋sin .‎ 又因为 sin α＝，且α∈，‎ 所以cos α＝－，‎ 所以f＝＋ ‎＝.‎ ‎12．解：(1)法一：∵cos＝coscos β＋sinsin β ‎＝cos β＋sin β＝，‎ ‎∴cos β＋sin β＝，∴1＋sin 2β＝，∴sin 2β＝－.‎ 法二：sin 2β＝cos＝2cos2－1＝－.‎ ‎(2)∵0<α<<β<π，‎ ‎∴<β－<π，<α＋β<，‎ ‎∴sin>0，cos(α＋β)<0.‎ ‎∵cos＝，sin(α＋β)＝，‎ ‎∴sin＝，cos(α＋β)＝－.‎ ‎∴cos＝cos ‎＝cos(α＋β)·cos＋sin(α＋β)sin ‎＝－×＋×＝.‎ B卷：增分提能 ‎1．解：(1)∵tan＝，‎ ‎∴tan α＝＝＝，‎ 由 解得sin α＝.‎ ‎(2)由(1)知cos α＝＝ ＝，‎ 又0<α<<β<π，∴β－α∈(0，π)，‎ 而cos(β－α)＝，‎ ‎∴sin(β－α)＝＝ ＝，‎ 于是sin β＝sin[α＋(β－α)]‎ ‎＝sin αcos(β－α)＋cos αsin(β－α)‎ ‎＝×＋×＝.‎ 又β∈，∴β＝.‎ ‎2．解：(1)依题意有f(x)＝a·b＝sin ωxcos φ＋cos ωxsin φ＝sin(ωx＋φ)．‎ ‎∵函数f(x)的最小正周期为2π，‎ ‎∴2π＝T＝，解得ω＝1.‎ 将点M代入函数f(x)的解析式，‎ 得sin＝.‎ ‎∵＜φ＜π，∴＜＋φ＜，‎ ‎∴＋φ＝，∴φ＝.‎ 故f(x)＝sin＝cos x.‎ ‎(2)依题意有cos α＝，cos β＝，而α，β∈，‎ ‎∴sin α＝ ＝，sin β＝ ＝，‎ ‎∴sin 2α＝2sin αcos α＝，‎ cos 2α＝cos2α－sin2α＝－＝－，‎ ‎∴f(2α－β)＝cos(2α－β)‎ ‎＝cos 2αcos β＋sin 2αsin β ‎＝×＋×＝.‎ ‎3．解：(1)∵角α的终边经过点P(－3，)，‎ ‎∴sin α＝，cos α＝－，tan α＝－.‎ ‎∴sin 2α－tan α＝2sin αcos α－tan α＝－＋＝－.‎ ‎(2)∵f(x)＝cos(x－α)cos α－sin(x－α)sin α＝cos x，x∈R，‎ ‎∴g(x)＝cos－2cos2x＝sin 2x－1－cos 2x＝2sin－1，‎ ‎∵0≤x≤，∴－≤2x－≤.‎ ‎∴－≤sin≤1，∴－2≤2sin－1≤1，‎ 故函数g(x)＝f－‎2f2(x)在区间上的取值范围是[－2,1]．‎