2018人教A版数学必修一《1 2页

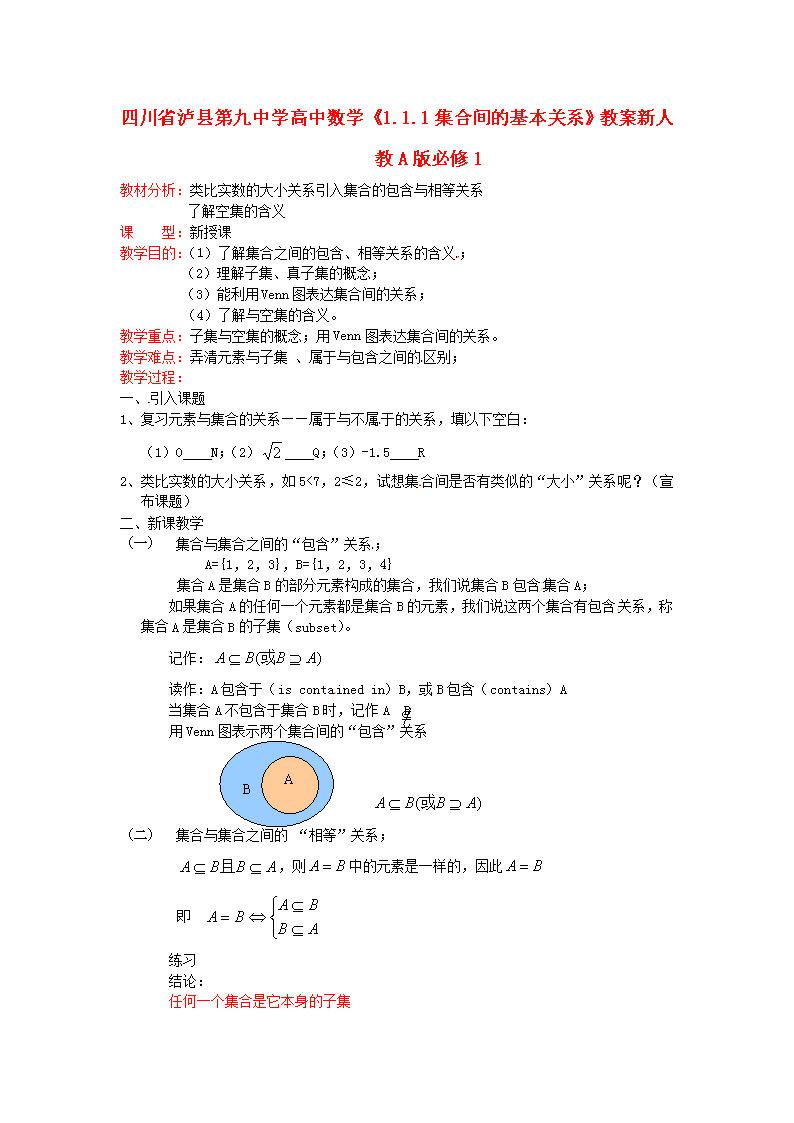
四川省泸县第九中学高中数学《‎1.1.1‎集合间的基本关系》教案 新人教A版必修1‎ 教材分析：类比实数的大小关系引入集合的包含与相等关系 了解空集的含义 课 型：新授课 教学目的：（1）了解集合之间的包含、相等关系的含义；‎ ‎（2）理解子集、真子集的概念；‎ ‎（3）能利用Venn图表达集合间的关系；‎ ‎（4）了解与空集的含义。‎ 教学重点：子集与空集的概念；用Venn图表达集合间的关系。‎ 教学难点：弄清元素与子集 、属于与包含之间的区别；‎ 教学过程：‎ 一、 引入课题 1、 复习元素与集合的关系——属于与不属于的关系，填以下空白：‎ ‎（1）0 N；（2） Q；（3）-1.5 R 2、 类比实数的大小关系，如5<7，2≤2，试想集合间是否有类似的“大小”关系呢？（宣布课题）‎ 二、 新课教学 （一） 集合与集合之间的“包含”关系；‎ A={1，2，3}，B={1，2，3，4}‎ 集合A是集合B的部分元素构成的集合，我们说集合B包含集合A；‎ 如果集合A的任何一个元素都是集合B的元素，我们说这两个集合有包含关系，称集合A是集合B的子集（subset）。‎ 记作：‎ 读作：A包含于（is contained in）B，或B包含（contains）A 当集合A不包含于集合B时，记作A B ‎ 用Venn图表示两个集合间的“包含”关系 B ‎ A ‎ ‎ （二） 集合与集合之间的 “相等”关系；‎ ‎，则中的元素是一样的，因此 即 ‎ 练习 结论：‎ 任何一个集合是它本身的子集 （一） 真子集的概念 若集合，存在元素，则称集合A是集合B的真子集（proper subset）。‎ 记作：A B（或B A）‎ 读作：A真包含于B（或B真包含A）‎ 举例（由学生举例，共同辨析）‎ （二） 空集的概念 ‎ （实例引入空集概念）‎ ‎ 不含有任何元素的集合称为空集（empty set），记作：‎ ‎ 规定：‎ ‎ 空集是任何集合的子集，是任何非空集合的真子集。‎ （三） 结论：‎ ，且，则 （四） 例题 ‎（1）写出集合{a，b}的所有的子集，并指出其中哪些是它的真子集。 （2）化简集合A={x|x-3>2},B={x|x5}，并表示A、B的关系；‎ （五） 课堂练习 （六） 归纳小结，强化思想 两个集合之间的基本关系只有“包含”与“相等”两种，可类比两个实数间的大小关系，同时还要注意区别“属于”与“包含”两种关系及其表示方法；‎ （七） 作业布置 1、 书面作业：习题1.1 第5题 2、 提高作业：‎ 已知集合，≥，且满足，求实数的取值范围。‎ 设集合，‎ ‎，试用Venn图表示它们之间的关系。‎ 板书设计（略）‎