2018-2019学年山东省临沂市罗庄区高一上学期期中质量调研数学试题 8页

‎2018-2019学年山东省临沂市罗庄区高一上学期期中质量调研数学试题 2018. 11 ‎ 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟. ‎ 注意事项：‎ ‎1.答卷前，考生务必将自己的班级、姓名、准考证号、考试科目及试卷类型用中性笔和2B铅笔分别涂写在答题卡上；‎ ‎2.将所有试题答案及解答过程一律填写在答题卡上.试题不交，只交答题卡.‎ 第I卷（选择题 共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.设全集，集合，，则 ‎ A. B. C. D. ‎ ‎2.下列四组函数中，表示同一函数的是 A. B. ‎ C. D. ‎ ‎3.下列选项正确的是 ‎ A. B. C. D. ‎ ‎4.已知是一次函数，且，则 ‎ A. B. C. D. 或 ‎5.幂函数的图象经过点，若，则下列各式正确的是 ‎ ‎ A. B. ‎ ‎ C. D. 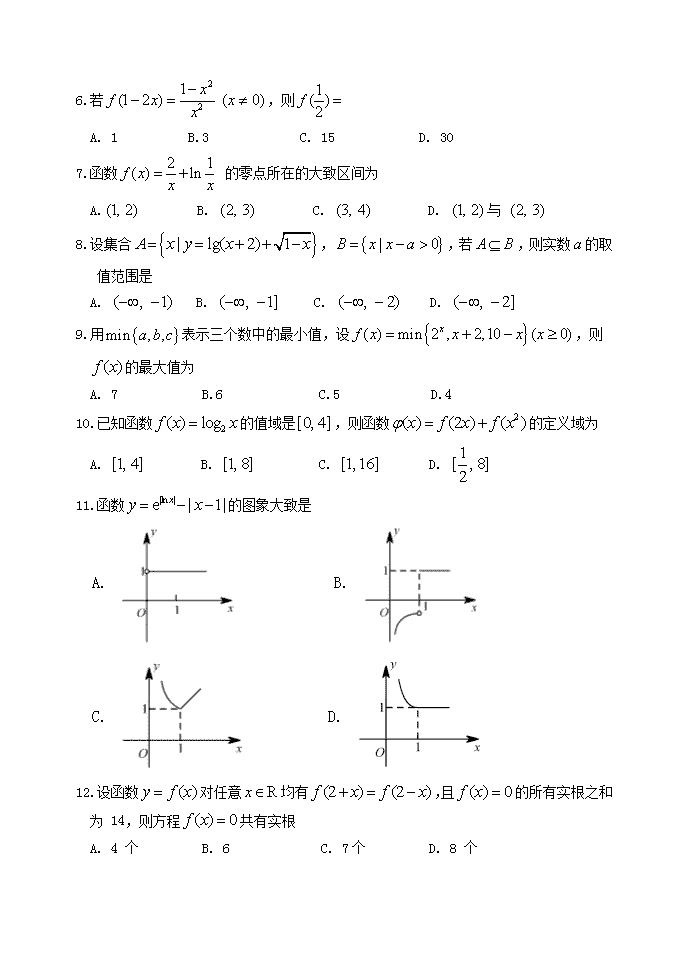‎ ‎6.若，则 A. 1 B.3 C. 15 D. 30‎ ‎7.函数 的零点所在的大致区间为 ‎ A. B. C. D. 与 ‎ ‎8.设集合，，若，则实数的取值范围是 ‎ A. B. C. D. ‎ ‎9.用表示三个数中的最小值，设，则的最大值为 ‎ A. 7 B.6 C.5 D.4‎ ‎10.已知函数的值域是，则函数的定义域为 A. B. C. D. ‎ ‎11.函数的图象大致是 ‎ A. B. ‎ C. D. ‎ ‎12.设函数对任意均有，且的所有实根之和为 14，则方程共有实根 A. 4 个 B. 6 C. 7个 D. 8 个 第II卷（非选择题 共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分.把正确答案填在答题纸给定的横线上. ‎ ‎13. 函数 的定义域是  ． ‎ ‎14. 已知函数的定义域为，且，则 ‎  ． ‎ ‎15. 已知函数，其中．如果函数恰有两个零点，那么实数的取值范围是  ． ‎ ‎16.已知函数是上的奇函数，函数在上是减函数，，则不等式的解集 . ‎ ‎ ‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程 ‎17. （本小题满分10分）‎ ‎ 已知集合，．‎ ‎（1）若，求；‎ ‎（2）若，求实数的取值范围．‎ ‎18.（本小题满分12分）‎ 已知函数（且），若函数的图象过点.‎ ‎（1）求的值及函数的零点；‎ ‎（2）求的解集.‎ ‎19. （本小题满分12分）‎ 若函数的定义域为. 当时，求的最值及相应的的值．‎ ‎20.（本小题满分12分）‎ 函数，（且），.‎ ‎（1）求的定义域，判断奇偶性；‎ ‎（2）若，求使得成立的的集合.‎ ‎21.（本小题满分12分）‎ ‎ 为了预防甲型流感，某学校对教室用药薰消毒法进行消毒，已知在药物释放过程中，室内每立方米空气中的含药量（毫克）与时间（小时）成正比；药物释放完毕后， 与的函数关系式为（为常数），其函数关系图象如下图所示．‎ ‎（1）写出从药物释放开始，每立方米空气中的含药量（毫克）与时间（小时）之间的函数关系式；‎ ‎（2）据测定，当空气中每立方米的含药量降低到0.25 毫克以下时，学生方可进教室，那么从药物释放开始，至少经过多少小时后学生才能回教室?‎ ‎22.（本小题满分12分）‎ 已知函数为奇函数．‎ ‎（1）求实数的值；‎ ‎（2）记集合，，判断与集合的关系；‎ ‎（3）当时，若函数的值域为，求的值.‎ 高一质量调研试题 ‎ ‎ 数学试题参考答案 2018. 11‎ 一、 选择题： CBDAA CBDBA DC 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13. 14. 15. 16. ‎ 三、解答题：本大题共6小题，共70分.‎ ‎17. 解：（1） 若，集合，…2分 ‎．‎ 则 ； …………5分 ‎（2） 若，则 ………………………………………8分 即， ‎ 所以实数的取值范围是． ………………………………………10分 ‎18.解：（1）因为函数图象过点，‎ 所以，. …………………………3分 函数，得. ………………………5分 所以函数的零点是.………………………………………………………………6分 ‎（2）由得，即， …………………………………9分 所以. ……………………11分 的解集为. ………………………………………………………12分 ‎19.解：　由，∴，‎ 解得或，∴， …………………………4分 ‎.‎ 令，‎ ‎∵，∴. ………………………………………6分 ‎∴()． ……………………7分 由二次函数性质可知：‎ 当时，， …………………………………8分 当时，， ………………………………………10分 当，即时，. ………………………11分 综上可知：当时，取到最大值为，无最小值．………12分 ‎ 20.解：（1）因为，‎ 由对数函数的定义，. ……………………………2分 所以函数的定义域为.………………………………………………3分 由得 ‎，‎ 所以是奇函数. …………………………………………………………6分 ‎（2）因为，所以. ………………………8分 ‎，‎ 由，所以，‎ 由的函数是增函数，所以，即，………………10分 又，所以. ………………………………………………11分 所以成立的的集合. …………………………12分 ‎21. 解：（1） 药物释放过程的函数关系式可设为， ……………1分 由于其图象过点，代入得，所以． ………3分 由于函数 的图象也过点，代入得 ， ……………4分 所以． …………………………………………5分 所以 . ……………………………………………6分 ‎      （2） 由题意可知，……………………………………………8分 整理得，………………………………………………………………10分 由函数是减函数，得，所以．……………………11分 答：至少经过0.6小时后，学生才能回教室. ……………………………………12分 ‎22．解: （1）∵为奇函数，∴ ，‎ 即 ‎ 即：R且,∴ . …………………………………4分 ‎（2）由（1）可知：，‎ 当时，；当时，‎ ‎∴， ……………………………………………………………………6分 而=，‎ ‎∴.………………………………………………………………………………8分 ‎(3) ∵，‎ ‎∴在上单调递增. ……………………………………………………9分 ‎∴，∴，即，‎ ‎∴m,n是方程的两个根， ………………………………………11分 又由题意可知，且，∴‎ ‎∴. …………………………………………………………12分