【数学】2018届一轮复习人教A版指数函数幂函数对数函数增长的比较问题学案 4页

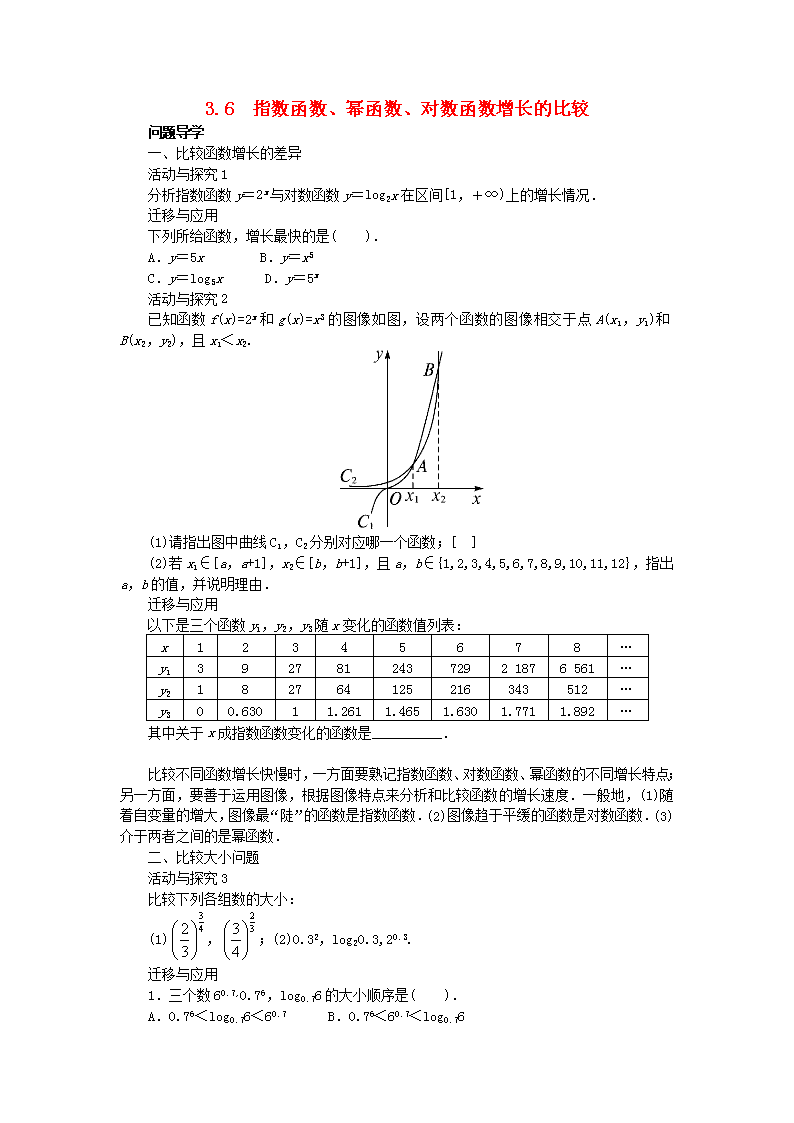
‎3.6　指数函数、幂函数、对数函数增长的比较 问题导学 一、比较函数增长的差异 活动与探究1‎ 分析指数函数y＝2x与对数函数y＝log2x在区间[1，＋∞)上的增长情况．‎ 迁移与应用 下列所给函数，增长最快的是(　　)．‎ A．y＝5x　　　　B．y＝x5‎ C．y＝log5x D．y＝5x 活动与探究2‎ 已知函数f(x)=2x和g(x)=x3的图像如图，设两个函数的图像相交于点A(x1，y1)和B(x2，y2)，且x1＜x2.‎ ‎(1)请指出图中曲线C1，C2分别对应哪一个函数；[ ]‎ ‎(2)若x1∈[a，a+1]，x2∈[b，b+1]，且a，b∈{1,2,3,4,5,6,7,8,9,10,11,12}，指出a，b的值，并说明理由．‎ 迁移与应用 以下是三个函数y1，y2，y3随x变化的函数值列表：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎…‎ y1‎ ‎3‎ ‎9 ‎ ‎27‎ ‎81‎ ‎243‎ ‎729‎ ‎2 187‎ ‎6 561‎ ‎…‎ y2‎ ‎1‎ ‎8‎ ‎27‎ ‎64‎ ‎125‎ ‎216‎ ‎343‎ ‎512‎ ‎…‎ y3‎ ‎0‎ ‎0.630‎ ‎1‎ ‎1.261‎ ‎1.465‎ ‎1.630‎ ‎1.771‎ ‎1.892‎ ‎…‎ 其中关于x成指数函数变化的函数是__________．‎ 比较不同函数增长快慢时，一方面要熟记指数函数、对数函数、幂函数的不同增长特点；另一方面，要善于运用图像，根据图像特点来分析和比较函数的增长速度．一般地，(1)随着自变量的增大，图像最“陡”的函数是指数函数．(2)图像趋于平缓的函数是对数函数．(3)介于两者之间的是幂函数．‎ 二、比较大小问题 活动与探究3‎ 比较下列各组数的大小：‎ ‎(1)，；(2)0.32，log20.3,20.3.‎ 迁移与应用 ‎1．三个数60.7,0.76，log0.76的大小顺序是(　　)．‎ A．0.76＜log0.76＜60.7 B．0.76＜60.7＜log0.76‎ C．log0.76＜60.7＜0.76 D．log0.76＜0.76＜60.7‎ ‎2．试比较a＝20.3，b＝0.32，c＝logx(x2＋0.3)(x＞1)的大小．‎ 解决这类题目的关键在于构造恰当的函数，若指数相同而底数不同，则考虑幂函数；若指数不同而底数相同，则考虑指数函数；若底数不同，指数也不同，需引入中间量，利用幂函数与指数函数的单调性，也可以借助幂函数与指数函数的图像．‎ 当堂检测 ‎1．下面对函数f(x)＝与g(x)＝在区间(0，＋∞)上的增减情况的说法中正确的是(　　)．‎ A．f(x)的增减速度越来越慢，g(x)的增减速度越来越快 ‎ B．f(x)的增减速度越来越快，g(x)的增减速度越来越慢 C．f(x)的增减速度越来越慢，g(x)的增减速度越来越慢 D．f(x)的增减速度越来越快，g(x)的增减速度越来越快 ‎2．当x越来越大时，下列函数中，增长速度最快的应该是(　　)．‎ A．y＝100x B．y＝log100x ‎ C．y＝x100 D．y＝100x ‎3．已知函数f(x)＝3x，g(x)＝2x，当x∈R时，有(　　)．‎ A．f(x)＞g(x)‎ B．g(x)＞f(x)‎ C．f(x)≥g(x)‎ D．g(x)≥f(x)‎ ‎4．函数y1＝2x与y2＝x2，当x＞0时，图像的交点个数是(　　)．‎ A．0 B．1‎ C．2 D．3‎ ‎5．当＜a＜1时，若x＝log‎2a，y＝log‎3a，z＝－‎2a，那么x，y，z之间的大小关系是__________．‎ 提示：用最精炼的语言把你当堂掌握的核心知识的精华部分和基本技能的要领部分写下来并进行识记。‎ 答案：‎ 课前预习导学 ‎【预习导引】‎ 大　小　大 预习交流　提示：存在，因为函数y＝ax(a＞1)，y＝logax(a＞1)，y＝xn(n＞0)在区间(0，＋∞)上都是增加的，但随着x的增大，y＝ax(a＞1)的增长速度越来越快，会超过并远远大于y＝xn(n＞0)的增长速度，而y＝logax(a＞1)的增长速度则会越来越慢，因此，总会存在一个x0，使得当x＞x0时，恒有logax＜xn＜ax.‎ 课堂合作探究[ ]‎ ‎【问题导学】 ‎ 活动与探究1　思路分析：解答本题时，应分析对于相同自变量的增量，比较指数函数的增量与对数函数的增量的差异．‎ 解：指数函数y＝2x，当x由x1＝1增加到x2＝3时，Δx＝2，Δy＝23－21＝6；‎ 对数函数y＝log2x，当x由x1＝1增加到x2＝3时，Δx＝2，而Δy＝log23－log21≈1.585 0.‎ 由此可知，在区间[1，＋∞)内，指数函数y＝2x随着x的增长，函数值的增长速度逐渐加快，而对数函数y＝log2x的增长速度逐渐变得很缓慢．‎ 迁移与应用　D ‎ 活动与探究2　思路分析：(1)由指数函数和幂函数不同的增长速度可判断曲线对应的函数；(2)通过计算比较函数值的大小关系，求出a，b的值．‎ 解：(1)根据指数函数与幂函数的增长速度知：C1对应函数g(x)＝x3，C2对应函数f(x)＝2x.‎ ‎(2)依题意知x1和x2是使两个函数的函数值相等的自变量x的值．当x＜x1时，2x＞x3，即f(x)＞g(x)；‎ 当x1＜x＜x2时，f(x)＜g(x)； ‎ 当x＞x2时，f(x)＞g(x)．‎ 由于f(1)＝2，g(1)＝1，f(2)＝22＝4，g(2)＝23＝8，‎ 所以x1∈[1,2]，即a＝1；‎ 又因为f(8)＝28＝256，g(8)＝83＝512，‎ f(8)＜g(8)，f(9)＝29＝512，‎ g(9)＝93＝729，f(9)＜g(9)．‎ f(10)＝210＝1 024，g(10)＝103＝1 000，f(10)＞g(10)，所以x2∈[9,10]，即b＝9.‎ 迁移与应用　y1　解析：指数函数中的增长量是成倍增加的，函数y1中增长量分别为6,18,54,162,486，1 458，4 374，…，是成倍增加的，因而y1呈指数变化．‎ 活动与探究3　思路分析：先观察各组数值的特点，然后考虑构造适当的函数，利用函数的性质或图像进行求解．‎ 解：(1)∵函数y1＝x为R上的减函数，又＞，∴.‎ 又函数y2＝在(0，＋∞)上是增加的，且＞，‎ ‎∴.∴.‎ ‎(2)令函数y1＝x2，y2＝log2x，y3＝2x.在同一坐标系内作出上述三个函数的图像如图，然后作直线x＝0.3，此直线必与上述三个函数图像相交．由图像知log20.3＜0.32＜20.3.‎ 迁移与应用　1．D　解析：∵60.7＞1,0＜0.76＜1，log0.76＜0，‎ ‎∴log0.76＜0.76＜60.7.‎ ‎2．解：1＜a＝20.3＜2，b＝0.32＜1，∵x＞1，‎ ‎∴c＝logx(x2＋0.3)＞logxx2＝2.∴b＜a＜c. ‎ ‎【当堂检测】‎ ‎1．C ‎2．D　解析：由于指数型函数的增长是爆炸式增长，则当x越来越大时，函数y＝100x的增长速度最快．‎ ‎3．A 解析：在同一直角坐标系中画出函数f(x)=3x，g(x)=2x的图像，如图所示，由于函数f(x)=3x的图像在函数g(x)=2x的图像的上方，则f(x)＞g(x)．‎ ‎4．C　解析：当x＝2、4时，y1＝y2，当x＞4时，y1＞y2.故交点个数是2.‎ ‎5．y＞x＞z　解析：画出函数y＝log2x，y＝log3x，y＝－2x的图像，由图像可知，当＜a＜1时，log‎3a＞log‎2a＞－‎2a，即y＞x＞z.‎