专题13 算法初步、推理与证明、复数 （捷进提升篇）-2017年高考数学备考中等生百日捷进提升系列 17页

【背一背重点知识】 1．算法的定义 算法是指按照 一定规则解决某一类问题的明确和有限的步骤． 2．程序框图 (1)程序框图又称 流程图 ，是一种用规定的程序、流程线及文字说明来准确、直观 地表示算法的图形． (2)程序框图通常由程序框和流程线组成． (3)基本的程序框有终端框(起止框) 、输入、输出框 、处框(执行框) 、判断框 ． 3．三种基本逻辑结构 顺序结构：由若干个依次执行的步骤组成的，这是任何一个算法都离不开的基本结构 条件结构：算法的流程根据条件是否成立 有不同的流向，条件结构就是处这种过程的结构 循环结构：从某处开始，按照一定的条件反复执行某些步骤的情况，反复执行的步骤称为循环 体 【讲一讲提高技能】 1. 必备技能： (1)控制循环结构的是计数变量和累加变量的变化规律以及循环结束的条件．在解答 这类题目时首先要弄清楚这两个变量的变化规律，其次要看清楚循环结束的条件， 这个条件由输出要求所决定，看清楚是满足条件时结束还是不满足条件时结束． (2)条件结构的程序框图中对判断条件的分类是逐级进行的，其中没有遗漏也没有重复，在解题 时对判断条件要仔细辨别，看清楚条件和函数的对应关系，对条件中的数值不要漏掉也不要重 复了端点值． 2. 典型例题： 例 1．．【河北省衡水中学 2017 届高三上学期第三次调，7】阅读如图所示的程序框图，则该算 法的功能是（ ） A．计算数列 前 5 项的和 B．计算数列 前 5 项的和 C．计算数列 前 6 项的和 D．计算数列 前 6 项的和 【答案】D 【解析】 考点：循环结构流程图． 【易错点睛】应用循环结构应注意的三个问题分别为：（1）确定循环变量和初始值；（2）确 定算法中反复执行的部分，即循环体；（3）确定循环的终止条件．同时依次计算出每次的循环 结果，直到不满足循环条件为止是解答此类问题的常用方法． 例 2．【云南省、四川省、贵州省 2017 届高三上学期百校大联考数学，9】右边程序框图的算法 思路来源于我国古代数学名著《数书九章》中的“秦九韶算法”求多项式的值．执行程序框图， 若输入 ， ， ， ，则输出的值为（ ） { }12n− { }2 1n − { }2 1n − { }12n− 0 1a = 1 1a = 2 0a = 3 1a = − 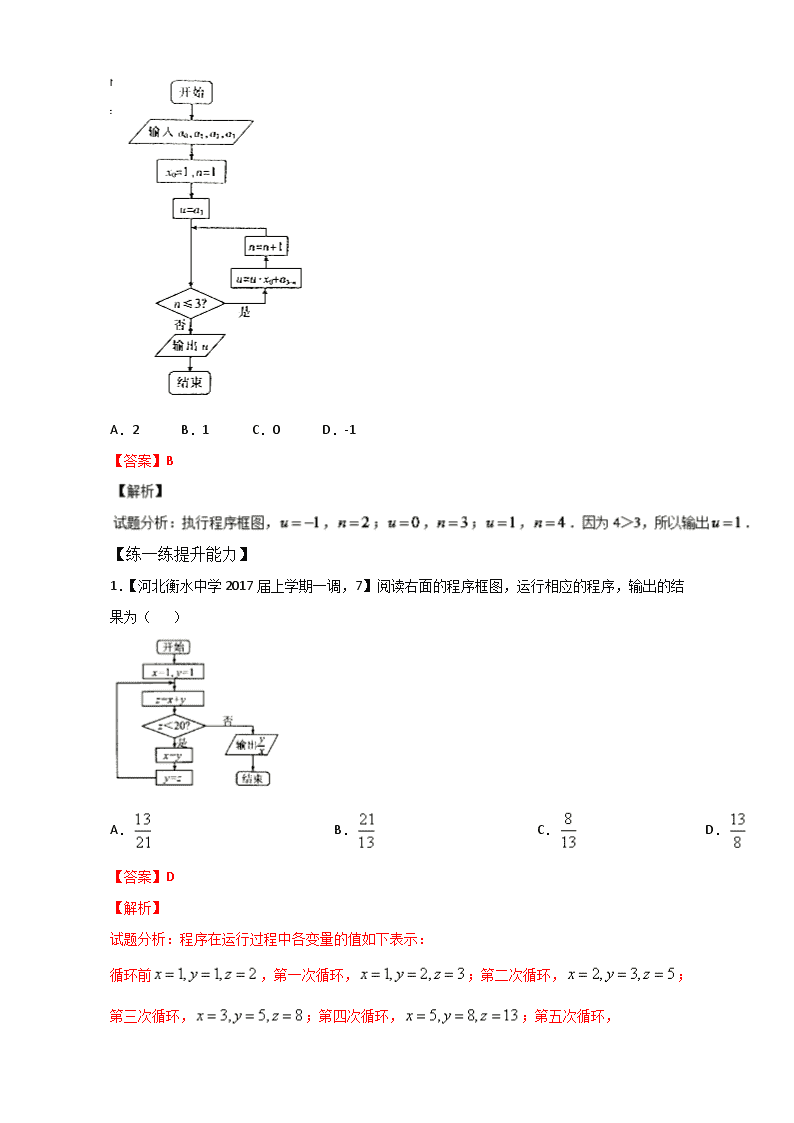A．2 B．1 C．0 D．-1 【答案】B 【练一练提升能力】 1．【河北衡水中学 2017 届上学期一调，7】阅读右面的程序框图，运行相应的程序，输出的结 果为（ ） A． B． C． D． 【答案】D 【解析】 试题分析：程序在运行过程中各变量的值如下表示： 循环前 ，第一次循环， ；第二次循环， ； 第三次循环， ；第四次循环， ；第五次循环， 13 21 21 13 8 13 13 8 1, 1, 2x y z= = = 1, 2, 3x y z= = = 2, 3, 5x y z= = = 3, 5, 8x y z= = = 5, 8, 13x y z= = = ；第六次时终止循环，此时输出结果 ，故选 D． 2．【河南省天一大联考 2017 届高三上学期阶段性测试（一）数学（理）试题】执行如图所示的 程序框图，如果输入的 ， ，则输出 的等于（ ） A ． 37 B ． 30 C ． 24 D．19 【答案】C 合情推与演绎推 【背一背重点知识】 1．合情推是根据已有的事实和正确的结论(包括定义、公、定等)，实验和实践的 结果，以及个人的经验和直觉等推测某些结果的推过程，归纳和类比是合情推常 见的方法，在解决问题的过程中，合情推具有猜测和发现结论、探索和提供思路 的作用，有利于创新意识的培养． 2．演绎推是指如果推是从一般性的原出发，推出某个特殊情况下的结论，我们 把这种推称为演绎推． 演绎推的一般模式是“三段论”，包括：①大前提；②小前提；③结论． 3．证明方法 (1)直接证明 ①综合法 2P = 1Q = M 8, 13, 21x y z= = = 12 8 y x = 一般地，利用已知条件和某些数学定义、定、公等，经过一系列的推论证，最后推 导出所要证明的结论成立，这种证明方法叫综合法．综合法又叫顺推法或由因导果 法． ②分析法 一般地，从要证明的结论出发，逐步寻求使它成立的充分条件，直至最后，把要证 明的结论归结为判定一个明显成立的条件(已知条件、定义、定、公等)，这种证明 方法叫分析法．分析法又叫逆推法或执果索因法． (2)间接证明——反证法 一般地，假设原命题不成立，经过正确的推，最后得出矛盾，因此说明假设错误， 从而证明原命题成立，这种证明方法叫反证法． (3)数学归纳法 一般地，证明一个与正整数 n 有关的命题，可按下列步骤进行： ①(归纳奠基)证明当 n 取第一个值 n0 (n0∈N*)时命题成立； ②(归纳递推)假设 n＝k (k≥n0，k∈N*)时命题成立，证明当 n＝k＋1 时命题也成 立． 只要完成这两个步骤，就可以断定命题对从 n0 开始的所有正整数 n 都成立．上述证 明方法叫做数学归纳法． 【讲一讲提高技能】 1．必备技能： A．归纳推的一般步骤是：(1)通过观察个别情况发现某些相同的性质；(2)从已知的相同性质中 推出一个明确表达的一般性命题(猜想)． B．类比推是由特殊到特殊的推，其一般步骤是： (1)找出两类事物之间的相似性或一致性； (2)用一类事物的性质去推测另一类事物的性质，得出一个明确的命题(猜想)． 类比是根据两个不同的对象，在某些方面(如特征、属性、关系等)的类同之处，猜测这两个对 象在其他方面也可能有类同之处，并作出某种判断的推方法．类比是科学研究最普遍的方法之 一．在数学中，类比是发现概念、方法、定和公式的重要手段，也是开拓新领域和创造新分支 的重要手段．类比在数学中应用广泛．数与式、平面与空间、一元与多元、低次与高次、相等 与不等、有限与无限之间有不少结论，都是先用类比法猜想，而后加以证明的． 类比推的关键是找到合适的类比对象，如上例中的椭圆类比到双曲线，常见的平面 几何中的一些定、公式、结论等，可以类比到立体几何中，得到类似的结论．一般 平面中的一些元素与空间中的一些元素的类比如表所示： 平面 空间 点 线 线 面 圆 球 三角形 三棱锥 角 二面角 面积 体积 周长 表面积 …… …… C．演绎推是由一般性的命题推出特殊性命题的一种推模式，是一种必然性推．演 绎推的前提与结论之间有蕴含关系，因而，只要前提是真实的，推的形式是正确的， 那么结论必定是真实的，但是错误的前提可能导致错误的结论． 演绎推的主要形式，就是由大前提、小前提推出结论的三段论式推．用集合论的观 点来讲，就是：若集合 M 的所有元素都具有性质 P，S 是 M 的子集，那么 S 中所有 元素都具有性质 P． D．合情推推出的结论不一定正确，有待进一步证明，演绎推在大前提、小前提和 推形式都正确的前提下得到的结论一定正确． 2．典型例题： 例 1．【河北省武邑中学 2017 届高三上学期第三次调研考试数学（理）试题】如图是网格工作 者经常用来解释网络运作的蛇形模型：数字出现在第行；数字 出现在第行，数字 (从 左至右) 出现在第行； 数字 出现在第行，依此类推，则第 行从左到右第个数字为 _________． 【答案】 例 2．【河南省天一大联考 2017 届高三上学期阶段性测试（一）数学（理）试题】6 月 23 日 15 2,3 6,5,4 7,8,9,10 20 194 时前后，江苏盐城阜宁、射阳等地突遭强冰雹、龙卷风双重灾害袭击，风力达 12 级．灾害发生后，有甲、乙、丙、丁 4 个轻型教授队从 ， ， ， 四个不同的方向前往 灾区． 已知下面四种说法都是正确的． （1）甲轻型教授队所在方向不是 方向，也不是 方向； （2）乙轻型教授队所在方向不是 方向，也不是 方向； （3）丙轻型教授队所在方向不是 方向，也不是 方向； （4）丁轻型教授队所在方向不是 方向，也不是 方向． 此外还可确定：如果丙所在方向不是 方向，那么甲所在方向就不是 方向．有下列判断： ①甲所在方向是 方向；②乙所在方向是 方向；③丙所在方向是 方向；④丁所在方向是 方向． 其中判断正确的序号是__________． 【答案】③ 【思路点晴】类比推理是由特殊到特殊的推理，是两类类似的对象之间的推理，其中一个对象 具有某个性质，则另一个对象也具有类似的性质．在进行类比时，要充分考虑已知对象性质的 推理过程，然后类比推导类比对象的性质．类比推理时要尽量从本质上去类比，不要被表面现 象迷惑，否则会犯机械类比的错误．演绎推理是由一般到特殊的推理，数学的证明过程主要是 通过演绎推理进行的，只要采用的演绎推理的大前提、小前提和推理形式是正确的，其结论一 定是正确，一定要注意推理过程的正确性与完备性． 【练一练提升能力】 1 ．【湖 北 黄 石 2017 届 高 三 9 月 调 研 ， 12 】 定 义 ： 如 果 函 数 在 上 存 在 满 足 ， ， 则 称 函 数 是 上的“双中值函数”，已知函数 是 上“双中值函 数”，则实数的取值范围是（ ） A． B． C． D． 【答案】A A B C D C D A B A B A D D A B D D C ( )f x [ ],a b ( )1 2 1 2,x x a x x b< < < ( ) ( ) ( ) 1 f b f af x b a −′ = − ( ) ( ) ( ) 2 f b f af x b a −′ = − ( )f x [ ],a b ( ) 3 22f x x x m= − + [ ]0,2a 1 1,8 4      1 1,12 4      1 1,12 8      1 ,18      【解析】 试 题 分 析 ： 由 题 意 得 在 上 有 两 个 不 等 的 实 根 ， 即 在 上有两个不等的实根，因此 ， 选 A． 2．【湖南省长沙市长郡中学 2017 届高三上学期第三次月考模拟数学（文）试题】设函数 ，观察： ， ， ， ， ……， 根据以上事实，当 时，由归纳推理可得： ． 【答案】 复数的概念、四则运算 【背一背重点知识】 1．复数的有关概念 ( ) ( ) ( )2 0 2 f a ff x a −′ = [ ]0,2a 2 23 4x x a a− = − [ ]0,2a 2 2 2 12 6 1 1 10 4 12 8 4 4 3(2 ) 2 a a a a a a a a  >  > − > − ⇒ < <  − < −  )0(22)( >+= xx xxf 22)()(1 +== x xxfxf 46))(()( 12 +== x xxffxf 814))(()( 23 +== x xxffxf 1630))(()( 34 +== x xxffxf ∗∈ Nn =)1(nf 123 1 n −× (1)复数的概念 形如 的数叫复数，其中 分别是它的实部和虚部．若 ，则 为实数，若 ，则 为虚数，若 ，则 为纯虚数． (2)复数相等： ⇔ ( )． (3)共轭复数： 与 共轭⇔ ，（ ） (4)复数的模 向量OZ→ 的模叫做复数 的模，记作 或 ，即 ＝ ＝ ． 2．复数的几何意义 (1)复平面的概念：建立直角坐标系来表示复数的平面叫做复平面． (2)实轴、虚轴：在复平面内，轴叫做实轴， 轴叫做虚轴，实轴上的点都表示实数； 除原点以外，虚轴上的点都表示纯虚数． (3)复数的几何表示： 复数 复平面内的点 平面向量 ． 3．复数的运算 (1)复数的加、减、乘、除运算法则 (2)复数加法的运算定律 复数的加法满足交换律、结合律． 【讲一讲提高技能】 1 必备技能： （1）复数的概念 对于复数 a＋bi(a，b∈R)，a 叫做实部，b 叫做虚部；当且仅当 b＝0 时，复数 a＋ bi(a，b∈R)是实数 a；当 b≠0 时，复数 a＋bi 叫做虚数；当 a＝0 且 b≠0 时，复数 a ＋bi 叫做纯虚数． （2）复数的运算法则与实数运算法则相同，主要是除法法则的运用，另外复数中 的几个常用结论应记熟：(1)(1±i)2＝±2i；(2) ； ；(3)i4n＝1；i4n＋1＝i； i4n＋2＝－1；i4n＋3＝－i； ( , )a bi a b R+ ∈ ,a b 0b = a bi+ 0b ≠ a bi+ 0, 0a b= ≠ a bi+ a bi c di+ = + ,a c b d= = , , ,a b c d R∉ a bi+ c di+ a c b d =  = − , , ,a b c d R∉ z a bi= + z a bi+ z a bi+ 2 2a b+ y z a bi= + →一一对应 ( , )Z a b →一一对应 OZ 1 =i1 i i + − 1 =-i1 i i − + i4n＋i4n＋1＋i4n＋2＋i4n＋3＝0；(4)设 ω＝ ，则 ω0＝1；ω2＝ ；ω3＝1；1＋ω ＋ω2＝0． 2 典型例题： 例 1．【湖南省长沙市长郡中学 2017 届高三摸底考试数学（理）试题】已知 （是 虚数单位），则等于（ ） A．-1 B．1 C．0 D． 【答案】B 【解析】 试题分析： ，则 ，所以 ．故选 B． 例 2．【江西省新余市第一中学 2017 届高三上学期调研考试（一）（开学考试）】已知是虚数单 位， 复数 在复平面内对应的点位于直线 上， 则复数的虚部为（ ） A． B． C． D． 【答案】D 【解析】 【方法点睛】本题重点考查复数的基本运算和复数的概念，属于基本题．首先对于复数的四则 运算，要切实掌握其运算技巧和常规思路，如 ．其次要熟悉复数相关基本概念，如复 数 的实部为、虚部为、模为 、对应点为 、共轭为 【练一练提升能力】 1．【浙江省温州市普通高中 2017 届高三 8 月模拟考试数学试题】已知是虚数单位，则满足 的复数在复平面上对应点所在的象限为（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 【答案】A 1 3± i2 2 − ω 20161( ) 2 iz −= 2 21 1 2( ) 22 i i i i − − += = − 41( ) 1 2 i− = 2016 4 5041 1( ) [( ) ] 1 2 2 i i− −= = ( )1z a Ra i = ∈− 2 0x y− = 1 5 i 1 5 ( )( ) ( ) ( ) ,( , , . )+ + = − + + ∈a bi c di ac bd ad bc i a b c d R ( , )+ ∈a bi a b R 2 2+a b ( , )a b .−a bi 3 4z i i− = + 【解析】 试题分析： ， ，对应点 ，在第一象限．故选 A． 2．【江苏省苏州市 2017 届高三暑假自主学习测试数学试题】已知是虚数单位，复数 z 的共轭 复数为，若 2z =+ 2 − 3，则 z = ▲ ． 【答案】 【解析】 试 题 分 析 ： 设 ， 则 （一）选择题（12*5=60 分） 1．【江苏省苏州市 2017 届高三暑假自主学习测试数学试题】如图是一个输出一列数的算法流 程图，则这列数的第三项是 ▲ ． 第 6 题图 【答案】30 2 ．【河 北 省 沧 州 市 第 一 中 学 2017 届 高 三 10 月 月 考 数 学 （ 理 ） 试 题 】 复 数 满 足 ，则 等于（ ） A．1 B． C．2 D．4 【答案】B 【解析】 2 23 4 3 4 5z i i− = + = + = 5z i= + (5,1) i−2 ( , )z a bi a b R= + ∈ 2 2 2 3 2 2,2 3 2, 1 1 .a bi a bi i a a b b a b z i+ = − + − ⇒ = + = − − ⇒ = = − ⇒ = − (2 ) 3i z i+ = − | |z 2 试题分析：因为 ，故 ，故应选 B． 3．【广东省惠州市 2017 届第二次调研考试数学（理）试题】若复数满足 ， 其中为虚数单位，则在复平面上复数对应的点的坐标为（ ） （A） （B） （C） （D） 【答案】D 【解析】 试题分析：z= ，故选 D． 4．【广东省惠州市 2017 届高三第一次调研考试数学（理）试题】执行如图的程序框图，则输出 的值为（ ） A．2 B． C． D． 【答案】A 5．【湖南省郴州市 2017 届高三上学期第一次教学质量监测数学（理）试题】设复数满足 （其中为虚数单位），则的模为（ ） A．1 B． C． D．3 【答案】A 【解析】 试题分析： ，故选 A． S 3− 1 2 − 1 3 (1 2 ) 2z i i− = + 2 5 | ||1 2 | | 2 | 5 | | 5 | | 1z i i z z− = + ⇒ = ⇒ = iiiii iz −=−=−−=+ −= 1)55(5 1)2)(3(5 1 2 3 211|| =+=z iiz 21+= )1,2( −− )1,2(− )1,2( )1,2( − 2 1 2 (1 2 )( ) 2i i i ii i + + −= = −− 6．观察下列各式： 则 A．28 B．76 C．123 D．199 【答案】C 【解析】等式右面的数构成一个数列 1，3，4，7，11，数列的前两项相加后面的项，即 ，所以可推出 ，选 C． 7．【江西省新余市 2016 届高三第二次模拟考试数学（理）试题】设复数 在复平面内的对 应点关于虚轴对称，若 ．是虚数单位，则 的虚部为（ ） A ． B ． C ． D． 【答案】D 8．【山西大学附中 2017 届高三第二次模拟测试数学（理）试题】阅读如图所示的程序如图， 运行相应的程序，若输出的 为 ，则判断框中填写的内容可以是（ ） A ． B ． C ． D． 【答案】C 【解析】 试题分析： ，判断是， ，判断是， ，判断是， S 11 12 6n = 6n < 6n ≤ 8n ≤ 0, 2S n= = 1 , 42S n= = 1 1 3 , 62 4 4S n= + = = 2 21, 3,a b a b+ = + = 3 3 4 4 5 54, 7, 11,a b a b a b+ = + = + =  10 10a b+ = 21 ++ =+ nnn aaa 12310 =a 21, zz iz 211 −= 1 2 z z 5 3 5 3− 5 4 5 4− ，判断否，输出 ，故填 ． 9．【河南省新乡市 2017 届高三上学期第一次调研测试数学（理）试题】已知复数 ， 则的虚部为（ ） A ． B ． C ． D． 【答案】D 【解析】 试题分析： ，虚部为 ． 10．【四川巴中市 2017 届“零诊”，3】设为虚数单位，则 的展开式中含 的项为（ ） A． B． C． D． 【答案】A． 【解析】 试 题 分 析 ： 由 二 项 展 开 的 通 项 公 式 ， 令 ， 故 的 系 数 是 ，故选 A． 11．若 是关于的实系数方程 的一个复数根，则（ ） A． B． C． D． 【答案】B 12．【河南省天一大联考 2016-2017 学年高中毕业班阶段性测试（二）数学（理）试题】对于正 整数，记 表示的最大奇数因数，例如 ， ， ．设 ． 给 出 下 列 四 个 结 论 ： ① ； ② ，都有 ；③ ；④ ， ， ．则其中所有正 确结论的序 号为（ ） 1 1 1 11, 82 4 6 12S n= + + = = S 6n ≤ 15 3 4 iz i = + 9 5 i− 9 5 i 9 5 − 9 5 ( ) ( )( ) 15 3 415 12 9 3 4 3 4 3 4 5 i ii iz i i i ⋅ − += = =+ + − 9 5 6)( ix − 4x 415x− 415x 420ix− 420ix 6 1 6 ( 1)r r r r rT C i x − + = − 2r = 4x 2 2 2 6 ( 1) 15C i− = − i21+ 02 =++ cbxx 3,2 == cb 3,2 =−= cb 1,2 −=−= cb 1,2 −== cb ( )g k (1) 1g = (2) 1g = (10) 5g = (1) (2) (3) (2 )n nS g g g g= + + + +… (3) (4) 10g g+ = *m N∀ ∈ (2 ) ( )g m g m= 1 2 3 30S S S+ + = 1 1 4n n nS S − −− = 2n ≥ *n N∈ A．①②③ B．②③④ C．③④ D．②④ 【答案】B （二）填空题（4*5=20 分） 13．【北京市 2017 届高三入学定位考试数学（文）试题】网上购鞋常常看到这样一张脚的长度 与鞋号的对照表，第一行可以理解为脚的长度，第二行是我们习惯称呼的“鞋号”． 从上述表格中可以推算出 30 号的童鞋对应的脚的长度为____；若一个篮球运动员的脚长为 282 ，则他该穿_____号的鞋． 【答案】 ， 【解析】 试题分析：观察上图可知，法实际标注 ，故 号的童鞋对应的脚的长度为 ， 当脚长为为 ，对应的法 ，应穿 码的鞋，故答案为 ， ． 14．已知 ，观察下列各式： mm mm020 47 100.2 −× 30 mm020 mm282 4.46102.0282 =−× 47 mm020 47 (0, )x∈ +∞ 类比得： ，则 ___________． 【答案】 15．【湖南永州市 2017 届高三第一次模拟，16】函数 的定义域为 ，若存在闭区间 ，使得函数 满足：（1） 在 上是单调函数；（2） 在 上 的值域为 ，则称区间 为函数 的“完美区间”．下列函数中存在“完美 区间”的是________（只需填符合题意的函数序号）． ① ； ② ； ③ ； ④ ． 【答案】①④ 【解析】 试题分析：由“完美区间”定义可知，若函数存在完美区间，则必满足 ，①若函数 存在“完美区间”，则 或，又函数 在 上单调递增，可知区 间 为函数 的；②由 ，可知方程只有一解，不满足；③ 无 解，不满足；④ ，解得 ，又函数 在 单调 递增，故存在 “完美区间”为 ． 16．【湖北省黄石市 2017 届高三年级九月份调研，16】将三项式 展开，当 时，得到如下左图所示的展开式，右图所示的广义杨辉三角形： 1 2,x x + ≥ 2 2 4 4 3,2 2 x xx x x + = + + ≥ 3 3 27 27 4,3 3 3 x x xx x x + = + + + ≥   *1( )n ax n n Nx + ≥ + ∈ a = nn ( )f x D [ , ]m n D⊆ ( )f x ( )f x [ , ]m n ( )f x [ , ]m n [2 ,2 ]m n [ , ]m n ( )y f x= 2( )f x x= 1 2 ( ) logf x x= ( ) xf x e= 1( ) 3f x x x = − + mmf 2)( = 2( )f x x= 022 ⇒= mm )(xf ]2,0[ ]2,0[ 2( )f x x= mm 2log 2 1 = mem 2= mmm 231 =+− 2 53±=m 1( ) 3f x x x = − + ),0( +∞ ]2 53,2 53[ +− ( )2 1 n x x+ + 1,2,3,n =  第 0 行 1 第 1 行 1 1 1 第 2 行 1 2 3 2 1 第 3 行 1 3 6 7 6 3 1 第 4 行 1 4 10 16 19 16 10 4 1 …… 观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法： 第 0 行为 1，以下各行每个数是它头上与左右两肩上 3 数（不足 3 数的，缺少的数计为 0）之和， 第行共有 个数．若在 的展开式中， 项的系数为 75，则实数的值 为___________． 【答案】2 ( )02 1 1x x+ + = ( )12 21 1x x x x+ + = + + ( )22 4 3 21 2 3 2 1x x x x x x+ + = + + + + ( )32 6 5 4 3 21 3 6 7 6 3 1x x x x x x x x+ + = + + + + + + ( )42 8 7 6 5 4 3 21 4 10 16 19 16 10 4 1x x x x x x x x x x+ + = + + + + + + + + 2 1k + ( )( )521 1ax x x+ + + 8x