高中数学选修2-2课件1_6微积分基本定理（1） 24页

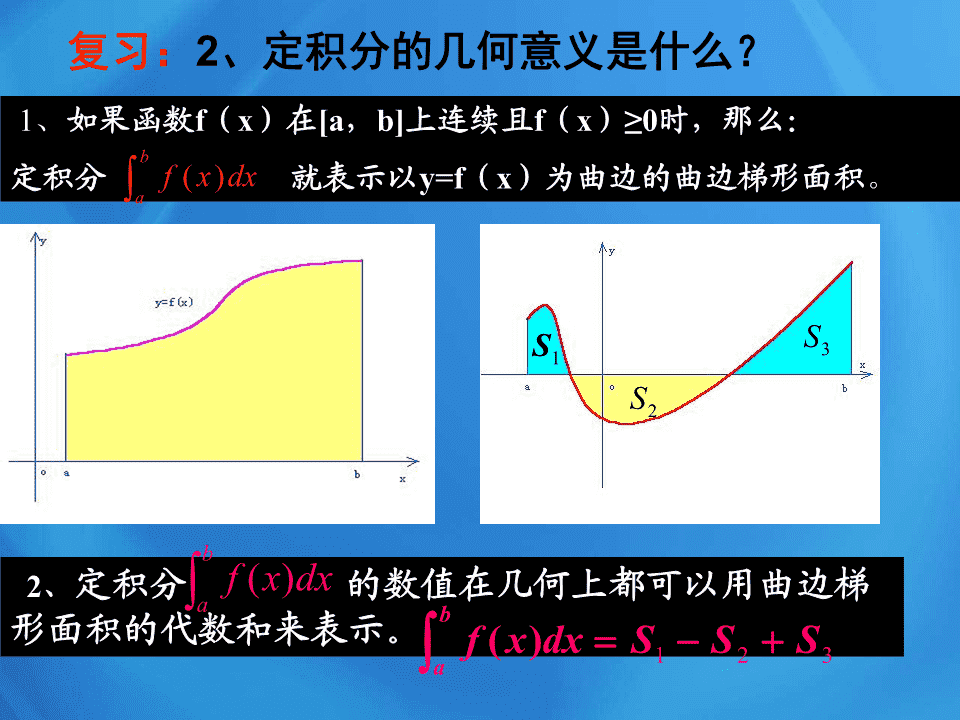
复习： 1 、 定积分是怎样定义？ 设函数 f （ x ）在 [a ， b] 上连续，在 [a ， b] 中任意插入 n-1 个分点： 把区间 [a,b] 等分成 n 个小区间， 则，这个常数 A 称为 f(x) 在 [a ， b] 上的 定积分 ( 简称积分 ) 记作 被积函数 被积表达式 积分变量 积分上限 积分下限 积分和 1 、 如果函数 f （ x ）在 [a ， b] 上连续且 f （ x ）≥ 0 时，那么： 定积分 就表示以 y=f （ x ）为曲边的曲边梯形面积 。 2 、 定积分 的数值在几何上都可以用曲边梯形面积的代数和来表示。 复习： 2 、定积分的几何意义是什么？ 曲边梯形的面积 曲边梯形的面积的负值 说明： 定积分的简单性质 题型 1 ： 定积分的简单性质的应用 点评： 运用定积分的性质可以化简定积分计算，也可以把一个函数的定积分化成几个简单函数定积分的和或差 题型 2 ： 定积分的几何意义的应用 8 问题 1 ： 你能求出下列格式的值吗？不妨试试。 问题 2 ： 一个作变速直线运动的物体的运动规律 S ＝ S(t) 。由导数的概念可以知道，它在任意时刻 t 的速度 v(t) ＝ S ’ （ t) 。设这个物体在时间段 〔a ， b〕 内的位移为 S ，你能分别用 S(t) ， v(t) 来表示 S 吗？ 从中你能发现导数和定积分的内在联系吗？ 另一方面，从 导数 角度来看： 如果已知该变速直线运动的路程函数为 s=s ( t ) ，则在时间区间 [ a,b ] 内物体的位移为 s ( b ) – s ( a ) ， 所以又有 由于 ，即 s ( t ) 是 v ( t ) 的原函数，这就是说，定积分 等于被积函数 v ( t) 的原函数 s ( t ) 在区间 [ a,b ] 上的增量 s ( b ) – s ( a ). 从 定积分 角度来看： 如果物体运动的速度函数为 v=v ( t ) ，那么在时间区间 [ a,b ] 内物体的位移 s 可以用定积分表示为 探究新知： O 微积分基本定理 微积分基本定理： 设函数 f ( x ) 在区间 [ a,b ] 上连续，并且 F’(x) ＝ f （ x) ，则， 这个结论叫 微积分基本定理 （ fundamental theorem of calculus) ，又叫 牛顿－莱布尼茨公式 （ Newton-Leibniz Formula). 说明： 牛顿－莱布尼茨公式 提供了计算定积分的简便的基本方法，即求定积分的值， 只要求出被积函数 f ( x ) 的一个原函数 F ( x ) ，然后 计算原函数在区间 [ a,b ] 上的增量 F ( b ) – F ( a ) 即可 . 该公式把计算定积分归结为求原函数的问题。 例 1 计算下列定积分 解 （１） 找出 f(x) 的原函数是关键 练习 1: 例２．计算定积分 解 : 达标练习 初等函数 微积分基本定理 三、小结 定积分公式 牛顿 牛顿，是英国伟大的数学家、物理学家、天文学家和自然哲学家。 1642 年 12 月 25 日生于英格兰林肯郡格兰瑟姆附近的沃尔索普村 ,1727 年 3 月 20 日在伦敦病逝。   牛顿 1661 年入英国剑桥大学三一学院， 1665 年获文学士学位。随后两年在家乡躲避瘟疫。这两年里，他制定了一生大多数重要科学创造的蓝图。 1667 年回剑桥后当选为三一学院院委，次年获硕士学位。 1669 年任卢卡斯教授直到 1701 年。 1696 年任皇家造币厂监督，并移居伦敦。 1703 年任英国皇家学会会长。 1706 年受女王安娜封爵。他晚年潜心于自然哲学与神学。   牛顿在科学上最卓越的贡献是微积分和经典力学的创建。 返回 莱布尼兹 莱布尼兹，德国数学家、哲学家，和牛顿 同为微积分的创始人； 1646 年 7 月 1 日生于 莱比锡， 1716 年 11 月 14 日卒于德国的汉诺 威。他父亲是莱比锡大学伦理学教授，家 庭丰富的藏书引起他广泛的兴趣。 1661 年 入莱比锡大学学习法律，又曾到耶拿大学 学习几何， 1666 年在纽伦堡阿尔特多夫取得法学博士学位。他当时写的论文 《 论组合的技巧 》 已含有数理逻 辑的早期思想，后来的工作使他成为数理逻辑的创始人。 1667 年他投身外交界，曾到欧洲各国游历。 1676 年到汉 诺威，任腓特烈公爵顾问及图书馆的馆长，并常居汉诺威，直到去世。莱布尼兹的多才多艺在历史上很少有 人能和他相比，他的著作包括数学、历史、语言、生物 、地质、机械、物理、法律、外交等各个方面。 返回 返回 基本初等函数的导数公式 返回