【数学】2020届一轮复习人教版（理）第6章第1讲不等关系与不等式的性质及一元二次不等式学案 13页

第六章　不等式 第1讲　不等关系与不等式的性质及一元二次不等式 ‎[考纲解读]　1.不等式性质是进行变形、证明、解不等式的依据，掌握不等式关系与性质及比较大小的常用方法：作差法与作商法．(重点)‎ ‎2.能从实际情景中抽象出一元二次不等式模型，通过函数图象了解一元二次不等式与相应的二次函数，一元二次方程之间的联系，能解一元二次不等式．(重点、难点)‎ ‎[考向预测]　从近三年高考情况来看，本讲是高考中的一个热点内容，但一般不会单独命题．预测2020年将会考查：利用不等式的性质判断结论的成立性，求参数的取值范围；一元二次不等式的解法，对含参数的二次不等式的分类讨论等．命题时常将不等式与函数的单调性相结合．试题一般以客观题的形式呈现，属中、低档题型.‎ ‎1．两个实数比较大小的依据 ‎ ‎ ‎2．不等式的基本性质 ‎ ‎ ‎3．必记结论 ‎(1)a>b，ab>0⇒<.‎ ‎(2)a<0b>0,0.‎ ‎(4)0b>0，m>0，则<；‎ >(b－m>0)；>；‎ <(b－m>0)．‎ ‎4．一元二次函数的三种形式 ‎(1)一般式：y＝ax2＋bx＋c(a≠0)．‎ ‎(2)顶点式：y＝a2＋(a≠0)．‎ ‎(3)两根式：y＝a(x－x1)(x－x2)(a≠0)．‎ ‎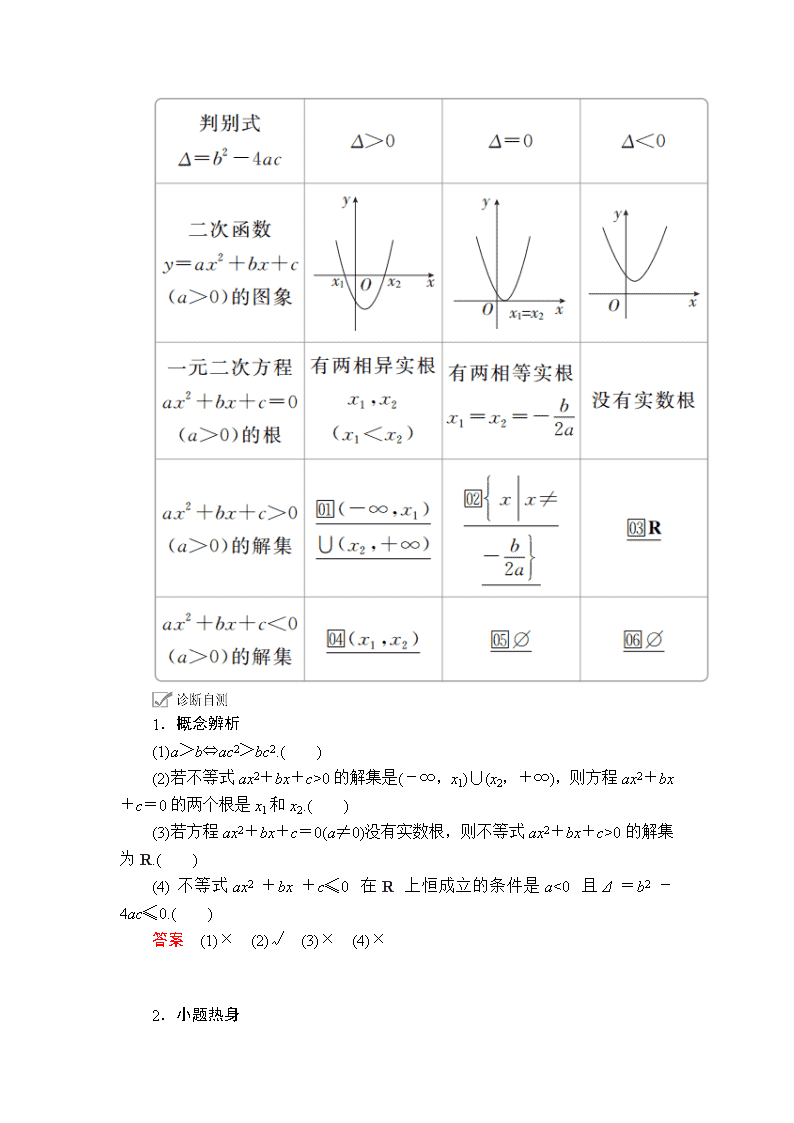5．三个二次之间的关系 ‎1．概念辨析 ‎(1)a＞b⇔ac2＞bc2.(　　)‎ ‎(2)若不等式ax2＋bx＋c>0的解集是(－∞，x1)∪(x2，＋∞)，则方程ax2＋bx＋c＝0的两个根是x1和x2.(　　)‎ ‎(3)若方程ax2＋bx＋c＝0(a≠0)没有实数根，则不等式ax2＋bx＋c>0的解集为R.(　　)‎ ‎(4)不等式ax2＋bx＋c≤0在R上恒成立的条件是a<0且Δ＝b2－4ac≤0.(　　)‎ 答案　(1)×　(2)√　(3)×　(4)×‎ ‎　 　　　　　　　　　　　　　　　　　　‎ ‎2．小题热身 ‎(1)设集合M＝{x|x2－3x－4<0}，N＝{x|0≤x≤5}，则M∩N等于(　　)‎ A．(0,4] B．[0,4)‎ C．[－1,0) D．(－1,0]‎ 答案　B 解析　因为M＝{x|－1ac B．c(b－a)<0‎ C．cb20‎ 答案　A 解析　因为c0，c<0.b的符号不确定，b－a<0，a－c>0，据此判断A成立，B，C，D不一定成立．‎ ‎(3)设M＝2a(a－2)，N＝(a＋1)(a－3)，则有(　　)‎ A．M>N B．M≥N C．M0，故M>N.‎ ‎(4)已知函数f(x)＝ax2＋ax－1，若对任意实数x，恒有f(x)≤0，则实数a的取值范围是________．‎ 答案　[－4,0]‎ 解析　当a＝0时，f(x)＝－1≤0成立，‎ 当a≠0时，若对∀x∈R，f(x)≤0，‎ 须有 解得－4≤a＜0.‎ 综上知，实数a的取值范围是[－4,0]．‎ 题型 　不等式性质的应用 ‎1．若a＞b＞0，c＜d＜0，则一定有(　　)‎ A.＞ B.＜ C.＞ D.＜ 答案　D 解析　解法一：⇒‎ ⇒＞⇒＜.故选D.‎ 解法二：依题意取a＝2，b＝1，c＝－2，d＝－1，‎ 代入验证得A，B，C均错误，只有D正确．故选D.‎ ‎2．已知等比数列{an}中，a1>0，q>0，前n项和为Sn，则与的大小关系为________．‎ 答案　< 解析　当q＝1时，＝3，＝5，所以<.‎ 当q>0且q≠1时，‎ －＝－ ‎＝＝<0，‎ 所以<.‎ 综上可知<.‎ ‎3．已知二次函数y＝f(x)的图象过原点，且1≤f(－1)≤2,3≤f(1)≤4，求f(－2)的取值范围．‎ 解　由题意知f(x)＝ax2＋bx，则f(－2)＝4a－2b，‎ 由f(－1)＝a－b，f(1)＝a＋b，‎ 设存在实数x，y，使得4a－2b＝x(a＋b)＋y(a－b)，‎ 即4a－2b＝(x＋y)a＋(x－y)b，‎ 所以解得 所以f(－2)＝4a－2b＝(a＋b)＋3(a－b)．‎ 又3≤a＋b≤4,3≤3(a－b)≤6，‎ 所以6≤(a＋b)＋3(a－b)≤10，‎ 即f(－2)的取值范围是[6,10]．‎ ‎1．判断不等式是否成立的方法 ‎(1)判断不等式是否成立，需要逐一给出推理判断或反例说明．‎ ‎(2)在判断一个关于不等式的命题的真假时，可结合不等式的性质，对数函数、指数函数的性质进行判断．‎ ‎2．比较两个数(式)大小的两种方法 ‎3．求代数式的取值范围 利用不等式性质求某些代数式的取值范围时，一般是利用整体思想，通过“一次性”不等关系的运算求得整体范围，是避免错误的有效途径．如举例说明3.　 　　　　　　　　　　　　　　　　　　‎ ‎1．若<<0，给出下列不等式：①<；②|a|＋b>0；③a－>b－；④ln a2>ln b2.其中正确的不等式是(　　)‎ A．①④ B．②③ C．①③ D．②④‎ 答案　C 解析　因为<<0，所以b|a|，所以|a|＋b<0，ln a2b，－>－可推出a－>b－，显然有<0<，综上知，①③正确，②④错误．‎ ‎2．若a>0，且a≠7，则(　　)‎ A．77aa<7aa7‎ B．77aa＝7aa7‎ C．77aa>7aa7‎ D．77aa与7aa7的大小不确定 答案　C 解析　显然77aa>0,7aa7>0，‎ 因为＝7·a＝7·－a＝7－a.‎ 当a>7时，0<<1,7－a<0，7－a>1，‎ 当01,7－a>0，7－a>1.‎ 综上知77aa>7aa7.‎ ‎3．若1<α<3，－4<β<2，则α－|β|的取值范围是________．‎ 答案　(－3,3)‎ 解析　∵－4<β<2，∴0≤|β|<4，∴－4<－|β|≤0.‎ ‎∴－3<α－|β|<3.‎ 题型 　不等式的解法 ‎1．函数f(x)＝的定义域是(　　)‎ A．(－∞，1)∪(3，＋∞) B．(1,3)‎ C．(－∞，2)∪(2，＋∞) D．(1,2)∪(2,3)‎ 答案　D 解析　由题意得 即解得10时，原不等式化为(x＋1)≥0，‎ 解得x≥或x≤－1.‎ ‎③当a<0时，原不等式化为(x＋1)≤0.‎ 当>－1，即a<－2时，解得－1≤x≤；‎ 当＝－1，即a＝－2时，解得x＝－1满足题意；‎ 当<－1，即0>a>－2，解得≤x≤－1.‎ 综上所述，当a＝0时，不等式的解集为{x|x≤－1}；‎ 当a>0时，不等式的解集为{x；‎ 当－21.‎ 若a<0，则原不等式等价于(x－1)>0，解得x<或x>1.‎ 若a>0，原不等式等价于(x－1)<0.‎ ‎①当a＝1时，＝1，(x－1)<0无解；‎ ‎②当a>1时，<1，解(x－1)<0得1，解(x－1)<0得11}；当01时，解集为{x.‎ ‎1．解一元二次不等式的四个步骤 ‎2．分式不等式的解法 求解分式不等式的关键是对原不等式进行恒等变形，转化为整式不等式(组)求解．‎ ‎(1)>0(<0)⇔f(x)·g(x)>0(<0)；如巩固迁移2.‎ ‎(2)≥0(≤0)⇔ ‎3.解含参数的一元二次不等式的一般步骤 ‎　 　　　　　　　　　　　　　　　　　　‎ ‎1．关于x的不等式x2－2ax－8a2<0(a>0)的解集为(x1，x2)，且x2－x1＝15，则a＝(　　)‎ A. B. C. D. 答案　A 解析　由条件知x1，x2为方程x2－2ax－8a2＝0的两根，则x1＋x2＝2a，x1x2＝－8a2.故(x2－x1)2＝(x1＋x2)2－4x1x2＝(2a)2－4×(－8a2)＝36a2＝152，得a＝，故选A.‎ ‎2．不等式≥－1的解集为________．‎ 答案　{x 解析　将原不等式移项通分得≥0，‎ 等价于解得x≤或x>5.‎ ‎∴原不等式的解集为{x.‎ 题型 　二次不等式中的任意性与存在性 角度1　任意性与存在性 ‎1．(1)若关于x的不等式x2－ax－a＞0的解集为(－∞，＋∞)，求实数a的取值范围；‎ ‎(2)若关于x的不等式x2－ax－a≤－3的解集不是空集，求实数a的取值范围．‎ 解　(1)设f(x)＝x2－ax－a，则关于x的不等式x2－ax－a＞0的解集为(－∞，＋∞)⇔f(x)＞0在(－∞，＋∞)上恒成立⇔f(x)min＞0，即f(x)min＝－＞0，解得－4＜a＜0(或用Δ<0)．‎ ‎(2)设f(x)＝x2－ax－a，则关于x的不等式x2－ax－a≤－3的解集不是空集⇔f(x)≤－3在(－∞，＋∞)上能成立⇔f(x)min≤－3，‎ 即f(x)min＝－≤－3，解得a≤－6或a≥2.‎ 角度2　给定区间上的任意性问题 ‎2．(1)已知函数f(x)＝x2＋mx－1，若对于任意x∈[m，m＋1]，都有f(x)<0成立，则实数m的取值范围是________．‎ ‎(2)设函数f(x)＝mx2－mx－1.若对于x∈[1,3]，f(x)<－m＋5恒成立，求m的取值范围．‎ 答案　(1)　(2)见解析 解析　(1)要满足f(x)＝x2＋mx－1＜0对于任意x∈[m，m＋1]恒成立，‎ 只需即 解得－＜m＜0.‎ ‎(2)要使f(x)<－m＋5在x∈[1,3]上恒成立，即 m2＋m－6<0在x∈[1,3]上恒成立．‎ 有以下两种方法：‎ 解法一：令g(x)＝m2＋m－6，x∈[1,3]．‎ 当m>0时，g(x)在[1,3]上是增函数，‎ 所以g(x)max＝g(3)，即7m－6<0，所以m<，‎ 所以00，‎ 又因为m(x2－x＋1)－6<0，所以m<.‎ 因为函数y＝＝ 在[1,3]上的最小值为，所以只需m<即可．‎ 所以m的取值范围是{m.‎ 角度3　给定参数范围的恒成立问题 ‎3．已知a∈[－1,1]时不等式x2＋(a－4)x＋4－2a＞0恒成立，则x的取值范围为(　　)‎ A．(－∞，2)∪(3，＋∞)‎ B．(－∞，1)∪(2，＋∞)‎ C．(－∞，1)∪(3，＋∞)‎ D．(1,3)‎ 答案　C 解析　把不等式的左端看成关于a的一次函数，记f(a)＝(x－2)a＋x2－4x＋4，‎ 则由f(a)＞0对于任意的a∈[－1,1]恒成立，‎ 所以f(－1)＝x2－5x＋6＞0，‎ 且f(1)＝x2－3x＋2＞0即可，解不等式组 得x＜1或x＞3.故选C.‎ 形如f(x)≥0(f(x)≤0)恒成立问题的求解思路 ‎(1)x∈R的不等式确定参数的范围时，结合二次函数的图象，利用判别式来求解．‎ ‎(2)x∈[a，b]的不等式确定参数范围时，①根据函数的单调性，求其最值，让最值大于等于或小于等于0，从而求参数的范围；②数形结合，利用二次函数在端点a，b处的取值特点确定不等式求范围．如举例说明2.‎ ‎(3)已知参数m∈[a，b]的不等式确定x的范围，要注意变换主元，一般地，知道谁的范围，就选谁当主元，求谁的范围，谁就是参数．如举例说明3.　 　　　　　　　　　　　　　　　　　　‎ ‎1．若不等式x2＋ax－2>0在区间[1,5]上有解，则a的取值范围是________．‎ 答案　 解析　由Δ＝a2＋8>0，知方程x2＋ax－2＝0恒有两个不等实数根，又知两根之积为负，所以方程x2＋ax－2＝0必有一正根、一负根．于是不等式在区间[1,5]上有解的充要条件是f(5)>0，解得a>－，故a的取值范围为.‎ ‎2．函数f(x)＝x2＋ax＋3.‎ ‎(1)当x∈R时，f(x)≥a恒成立，求实数a的取值范围；‎ ‎(2)当x∈[－2,2]时，f(x)≥a恒成立，求实数a的取值范围；‎ ‎(3)当a∈[4,6]时，f(x)≥0恒成立，求实数x的取值范围．‎ 解　(1)∵当x∈R时，x2＋ax＋3－a≥0恒成立，‎ 需Δ＝a2－4(3－a)≤0，即a2＋4a－12≤0，‎ ‎∴实数a的取值范围是[－6,2]．‎ ‎(2)当x∈[－2,2]时，设g(x)＝x2＋ax＋3－a≥0，分如下三种情况讨论(如图所示)：‎ ‎①如图1，当g(x)的图象恒在x轴上方且满足条件时，有Δ＝a2－4(3－a)≤0，即－6≤a≤2.‎ ‎②如图2，g(x)的图象与x轴有交点，‎ 但当x∈[－2，＋∞)时，g(x)≥0，‎ 即即 可得解得a∈∅.‎ ‎③如图3，g(x)的图象与x轴有交点，但当x∈(－∞，2]时，g(x)≥0.‎ 即即 可得∴－7≤a≤－6.‎ 综上，实数a的取值范围是[－7,2]．‎ ‎(3)令h(a)＝xa＋x2＋3.‎ 当a∈[4,6]时，h(a)≥0恒成立．‎ 只需即 解得x≤－3－或x≥－3＋.‎ ‎∴实数x的取值范围是(－∞，－3－]∪[－3＋，＋∞)．‎