- 619.50 KB
- 2021-06-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
« 绝密 启用前
2017—2018学年度第一学期高二期中考试
理科数学
命题人:冯智颖 王彩凤 审题人:吴统胜 禤铭东
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知直线的方程为,则该直线的斜率为( ) .
2.圆的圆心到直线的距离为1,则( ).
3. 经过原点O 作圆的切线,切线长是 ( ).
4.已知点的坐标为,直线的方程为,则点关于的对称点的坐标为( )
. . . .
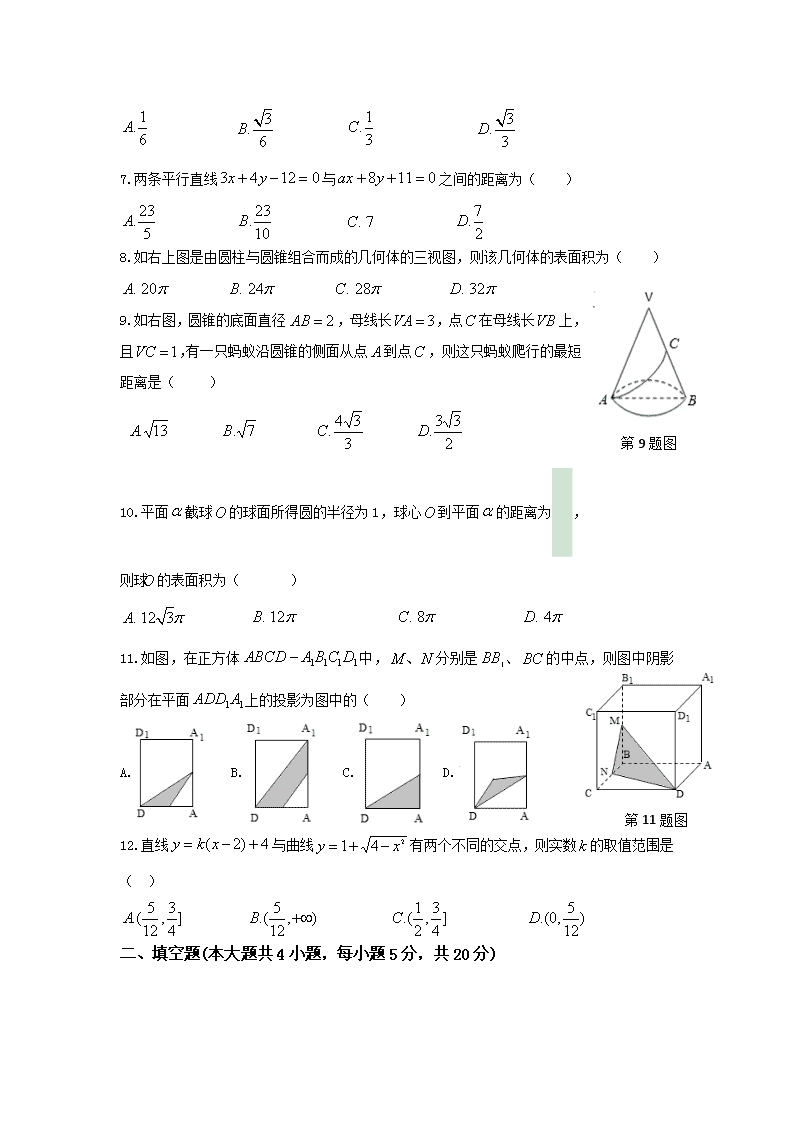
第8题图
5.下列命题中,表示两条不同的直线,、、表示三个不同的平面.
①若,,则; ②若,,则;
③若,,则; ④若,,,则.
正确的命题是( )
. ①③ . ②③ . ①④ . ②④
6. 已知正四面体中,是的中点,则异面直线所成角的余弦值为( )
7.两条平行直线与之间的距离为( )
8.如右上图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
第9题图
9.如右图,圆锥的底面直径,母线长,点在母线长上,且,有一只蚂蚁沿圆锥的侧面从点到点,则这只蚂蚁爬行的最短距离是( )
10.平面截球的球面所得圆的半径为1,球心到平面的距离为,则球的表面积为( )
第11题图
11.如图,在正方体中,分别是、的中点,则图中阴影部分在平面上的投影为图中的( )
A. B. C. D.
12.直线与曲线有两个不同的交点,则实数的取值范围是( )
二、填空题(本大题共4小题,每小题5分,共20分)
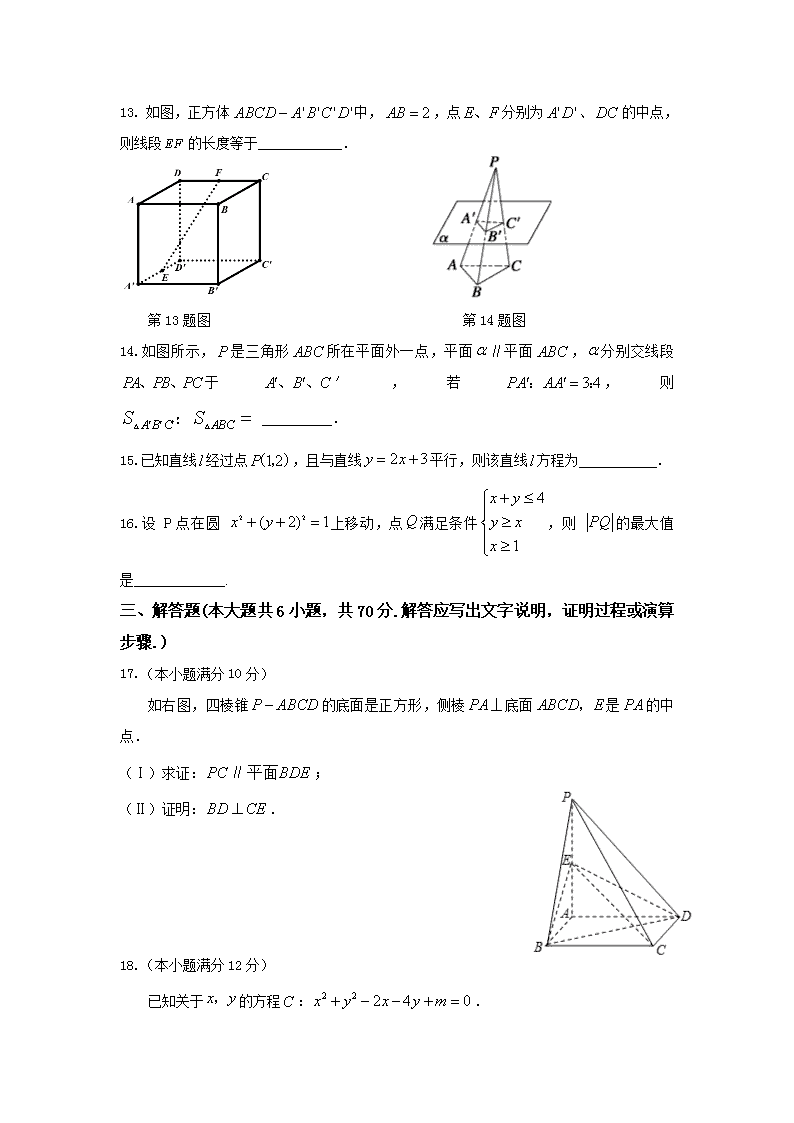
13.如图,正方体中,,点分别为、的中点,则线段的长度等于____________.
第13题图 第14题图
14.如图所示,是三角形所在平面外一点,平面∥平面,分别交线段于′,若,则 .
15.已知直线经过点,且与直线平行,则该直线方程为 .
16.设 P点在圆 上移动,点满足条件,则 的最大值是 .
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分10分)
如右图,四棱锥的底面是正方形,侧棱⊥底面是的中点.
(Ⅰ)求证:∥;
(Ⅱ)证明:.
18.(本小题满分12分)
已知关于的方程:.
(1)若方程表示圆,求的取值范围;
(2)若圆与圆外切,求的值;
19.(本小题满分12分)
如图,已知面垂直于圆柱底面,为底面直径,是底面圆周上异于的一点,. 求证:
(1);
(2)求几何体的最大体积.
20.(本小题满分12分)
已知的三个顶点为,为的中点.求: []
(1)所在直线的方程;
(2)边上中线所在直线的方程;
(3)边上的垂直平分线的方程.
21.(本小题满分12分)
如图,在四棱锥中,,为的中点,为的中点,底面是菱形,对角线交于,,求证:
(1) 平面;
(2)求二面角的余弦值.
22.(本小题满分12分)
已知圆,直线.
(1)求证:对,直线l与圆总有两个不同的交点、;
(2)求弦的中点的轨迹方程,并说明其轨迹是什么曲线;
(3)是否存在实数,使得圆上有四点到直线l的距离为?若存在,求出的范围;若不存在,说明理由.
2017—2018学年度第一学期高二期中考试理科数学答案
命题人:冯智颖 王彩凤 审题人:吴统胜 禤铭东
一、选择题(本大题共12小题,每小题5分,共60分)
1.B 2.A 3.A 4.B 5.C 6.B
7.D 8.C 9.B 10.B 11.A 12.A
二、填空题(本大题共4小题,每小题5分,共20分)
13. 14. 9:49
15.y=2x 16.
三、解答题(本大题共6小题,共70分)
17. (本小题满分10分)
证明:(Ⅰ)连结AC交BD于O,连结OE,
因为四边形ABCD是正方形,所以O为AC中点.…… (1分)
又因为E是PA的中点,所以PC∥OE,…………………(3分)
因为PC⊄平面BDE,OE⊂平面BDE, …………………(4分)
所以PC∥平面BDE.………………………………………(5分)
(Ⅱ)因为四边形ABCD是正方形,所以BD⊥AC.……(6分)
因为PA⊥底面ABCD,且BD⊂平面ABCD, 所以PA⊥BD.…………………………(8分)
又AC∩PA=A,AC⊂平面PAC,PA⊂平面PAC,所以BD⊥平面PAC…………………(9分)
又CE⊂平面PAC, 所以BD⊥CE.……………………………………………………(10分)
18.(本小题满分12分)
解:(1)把方程C:x2+y2-2x-4y+m=0,配方得:(x-1)2+(y-2)
2=5-m, ……… (3分)
若方程C表示圆,则5-m>0,解得m<5; ……………………………………………(5分)
(2)把圆x2+y2-8x-12y+36=0化为标准方程得:(x-4)2+(y-6)2=16, ……… (7分)
得到圆心坐标(4,6),半径为4, ……………………………………………………(8分)
则两圆心间的距离d==5,………………………………………(10分)
因为两圆的位置关系是外切,所以d=R+r即4+=5,解得m=4.……………(12分)
19.(本小题满分12分)
(1)证明:因为C是底面圆周上异于A,B的一点,AB是底面圆的直径,
所以AC⊥BC. ………………………………………………………………………………(1分)
因为AA1⊥平面ABC,BC⊂平面ABC,所以AA1⊥BC, ………………………………(3分)
而AC∩AA1=A,所以BC⊥平面AA1C. …………………………………………………(5分)
又BC⊂平面BA1C,所以平面AA1C⊥平面BA1C.………………………………………(6分)
(2)解:在Rt△ABC中,当AB边上的高最大时,三角形ABC面积最大,
此时
AC=BC.…………………………………………………………………………………(7分)
此时几何体取得最大体积.………………………………………………………(8分)
则由AB2=AC2+BC2且AC=BC, 得,…………………………………(10分)
所以. …………………………………(12分)
20.(本小题满分12分)
解:(1)因为直线BC经过B(2,1)和C(-2,3)两点,
由两点式得BC的方程为y-1=(x-2),…………………………………………………(2分)
即x+2y-4=0. ………………………………………………………………………………(4分)
(2)设BC中点D的坐标为(x,y),则x==0,y==2. …………………………(6分)
BC边的中线AD过点A(-3,0),D(0,2)两点,由截距式得
AD所在直线方程为+=1,即2x-3y+6=0. …………………………………………(8分)
(3)BC的斜率k1=-,则BC的垂直平分线DE的斜率k2=2,…………………………(10分)
由斜截式得直线DE的方程为y=2x+2. ………………………………………………(12分)
21.(本小题满分12分)
解:(1)因为菱形ABCD,所以O为AC和BD的中点.
因为为的中点,O为AC的中点,所以EO∥PC …………………………………(1分)
又EO平面PCD,PC⊂平面PCD,所以EO∥平面PCD ………………………………(2分)
因为F为BC的中点,O为BD的中点,所以FO∥CD. …………………………………(3分)
又FO平面PCD,PC⊂平面PCD,所以FO∥平面PCD,……………………………(4分)
又EO∩FO=O ,EO⊂平面EFO,FO⊂平面EFO………………………………………(5分)
所以,平面EFO∥平面PCD. ……………………………………………………………(6分)(2)EA平面ABCD,所以EAOF
过A作AMFO交FO的延长线于M,连接EM,所以FO
平面AEM,所以FOEM,
所以∠EMA为二面角B-OF-E的平面角……………………(8分)
又PA=AD=1,所以AE=,……………………(9分)[]
设FO交AC于Q,又,易知为等边三角形,所以,………………………(10分)
在中,,所以.………………………………………………………………(12分)
22.(本小题满分12分)
解:(1)圆C:(x+2)2+y2=5的圆心为C(-2,0),半径为,所以圆心C到直线l:mx-y+1+2m=0的距离.………………………………………………………(2分)
所以直线l与圆C相交,即直线l与圆C总有两个不同的交点;………………………(3分)
(2)设中点为M(x,y),因为直线l:mx-y+1+2m=0恒过定点(-2,1),………(4分)
当直线l的斜率存在时,,又,kAB•kMC=-1,
所以,化简得.…………………………(6分)
当直线l的斜率不存在时,中点M(-2,0)也满足上述方程.………………………(7分)
所以M的轨迹方程是,它是一个以为圆心,以为半径的圆.……………………………………………………………………………………………(8分)
(3)假设存在直线l,使得圆上有四点到直线l的距离为,由于圆心C(-2,0),半径为,则圆心C(-2,0)到直线l的距离为 ……(11分)
化简得m2>4,解得m>2或m<-2.…………………………………………………(12分)