2017年高考数学（理,山东）二轮专题复习（教师用书）名师寄语 第2点 回避“套路”解题，强化思维训练 2页

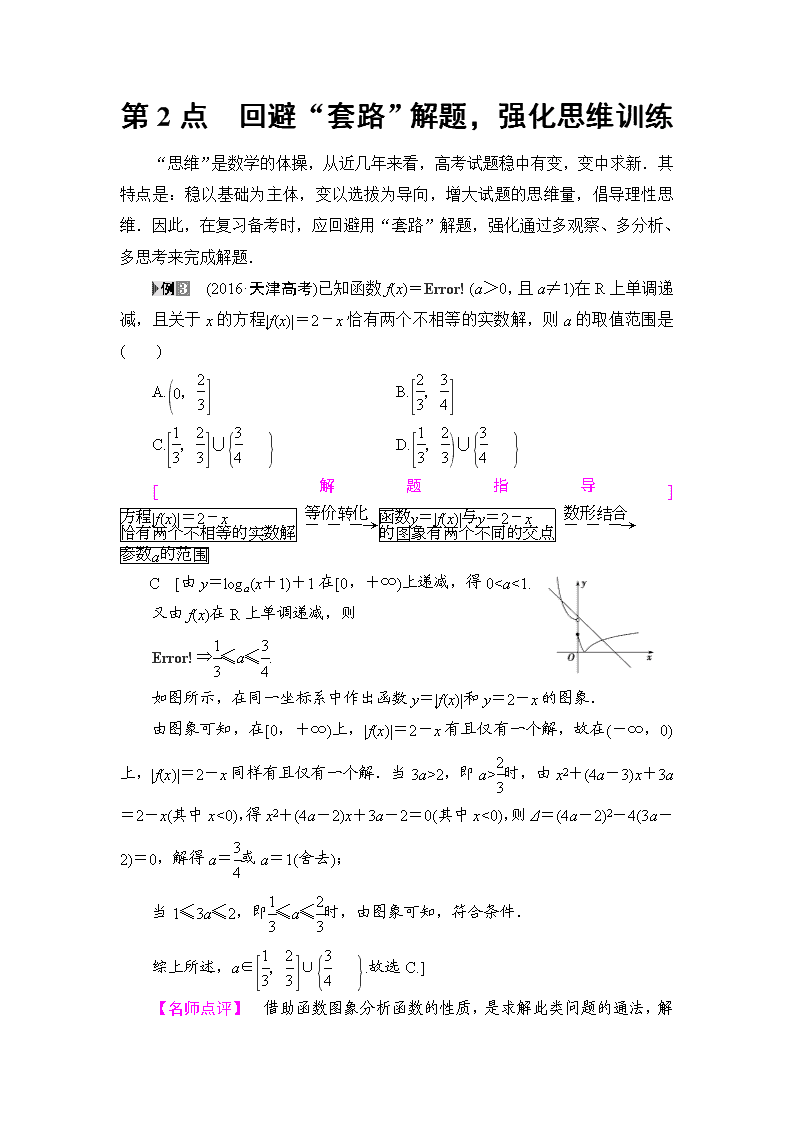
第 2 点　回避“套路”解题，强化思维训练 “思维”是数学的体操，从近几年来看，高考试题稳中有变，变中求新．其 特点是：稳以基础为主体，变以选拔为导向，增大试题的思维量，倡导理性思 维．因此，在复习备考时，应回避用“套路”解题，强化通过多观察、多分析、 多思考来完成解题． 　(2016·天津高考)已知函数 f(x)＝Error!(a＞0，且 a≠1)在 R 上单调递 减，且关于 x 的方程|f(x)|＝2－x 恰有两个不相等的实数解，则 a 的取值范围是 (　　) A.(0，2 3] B.[2 3 ，3 4] C.[1 3 ，2 3]∪{3 4 } D.[1 3 ，2 3)∪{3 4 } [ 解 题 指 导 ] 　 方程|f(x)|＝2－x 恰有两个不相等的实数解 ― ― ―→等价转化 函数y＝|f(x)|与y＝2－x 的图象有两个不同的交点 ― ― ―→数形结合 参数a的范围 C　[由 y＝loga(x＋1)＋1 在[0，＋∞)上递减，得 02，即 a>2 3 时，由 x2＋(4a－3)x＋3a ＝2－x(其中 x<0)，得 x2＋(4a－2)x＋3a－2＝0(其中 x<0)，则 Δ＝(4a－2)2－4(3a－ 2)＝0，解得 a＝3 4 或 a＝1(舍去)； 当 1≤3a≤2，即1 3 ≤a≤2 3 时，由图象可知，符合条件． 综上所述，a∈[1 3 ，2 3]∪{3 4 }.故选 C.] 【名师点评】　借助函数图象分析函数的性质，是求解此类问题的通法，解 题时，往往需要从函数的图象变化趋势中寻求解题的切入点，其中分段函数的单 调性是本题的易错点. 从以上典例我们可以看出，考能力不是考解题套路，而是考动手操作、深入 思考、灵活运用的能力(即分析问题和解决问题的能力)，考生需要通过眼、手、 脑高度的配合才能完成解题．因此，在二轮专题复习中，把握考查方向，强化思 维训练非常重要．