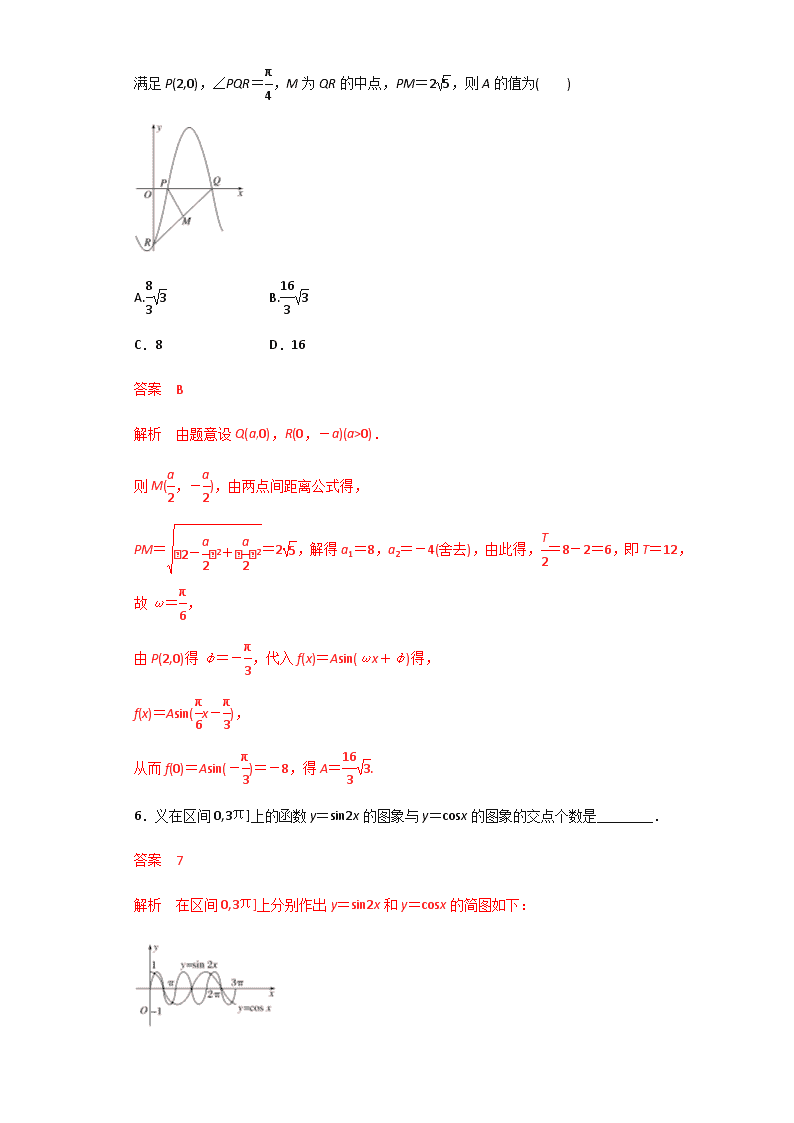专题06 三角函数的图像与性质-2017年高考数学（文）备考黄金易错点 19页

专题06 三角函数的图像与性质 ‎2017年高考数学（文）备考学易黄金易错点 ‎1．为了得到函数y＝sin的图象，只需把函数y＝sin2x的图象上所有的点(　　)‎ A．向左平行移动个单位长度 B．向右平行移动个单位长度 C．向左平行移动个单位长度 D．向右平行移动个单位长度 答案　D 解析　由题意可知，y＝sin＝sin，则只需把y＝sin 2x的图象向右平移个单位，故选D.‎ ‎2．若将函数y＝2sin2x的图象向左平移个单位长度，则平移后图象的对称轴为(　　)‎ A．x＝－(k∈Z) B．x＝＋(k∈Z)‎ C．x＝－(k∈Z) D．x＝＋(k∈Z)‎ 答案　B 解析　由题意将函数y＝2sin2x的图象向左平移个单位长度后得到函数的解析式为y＝2sin，由2x＋＝kπ＋，k∈Z，得函数的对称轴为x＝＋(k∈Z)，故选B.‎ ‎3．已知函数f(x)＝sin(ωx＋φ)，x＝－为f(x)的零点，x＝为y＝f(x)图象的对称轴，且f(x)在上单调，则ω的最大值为(　　)‎ A．11B．9C．7D．5‎ 答案　B 解析　因为x＝－为f(x)的零点，x＝为f(x)的图象的对称轴，所以－＝＋kT，即＝T＝·，所以ω＝4k＋1(k∈N)，又因为f(x)在上单调，所以－＝≤＝，即ω≤12，由此得ω的最大值为9，故选B.‎ ‎4．已知函数f(x)＝sin(x∈R，ω>0)图象的相邻两条对称轴之间的距离为.为了得到函数g(x)＝cosωx的图象，只要将y＝f(x)的图象(　　)‎ A．向左平移个单位长度 B．向右平移个单位长度 C．向左平移个单位长度 D．向右平移个单位长度 答案　A ‎5．如图，函数f(x)＝Asin(ωx＋φ)(其中A>0，ω>0，|φ|≤)与坐标轴的三个交点P、Q、R满足P(2,0)，∠PQR＝，M为QR的中点，PM＝2，则A的值为(　　)‎ A. B. C．8 D．16‎ 答案　B 解析　由题意设Q(a,0)，R(0，－a)(a>0)．‎ 则M(，－)，由两点间距离公式得，‎ PM＝＝2，解得a1＝8，a2＝－4(舍去)，由此得，＝8－2＝6，即T＝12，故ω＝，‎ 由P(2,0)得φ＝－，代入f(x)＝Asin(ωx＋φ)得，‎ f(x)＝Asin(x－)，‎ 从而f(0)＝Asin(－)＝－8，得A＝.‎ ‎6．义在区间0,3π]上的函数y＝sin2x的图象与y＝cosx的图象的交点个数是________．‎ 答案　7‎ 解析　在区间0,3π]上分别作出y＝sin2x和y＝cosx的简图如下：‎ 由图象可得两图象有7个交点．‎ ‎7．已知函数f(x)＝2asinωx·cosωx＋2cos2ωx－ (a>0，ω>0)的最大值为2，x1，x2是集合 M＝{x∈R|f(x)＝0}中的任意两个元素，且|x1－x2|的最小值为6.‎ ‎(1)求函数f(x)的解析式及其图象的对称轴方程；‎ ‎(2)将函数y＝f(x)的图象向右平移2个单位后得到函数y＝g(x)的图象，当x∈(－1,2]时，求函数h(x)＝f(x)·g(x)的值域．‎ 解　(1)f(x)＝2asinωx·cosωx＋2cos2ωx－＝asin2ωx＋cos2ωx.‎ 由题意知f(x)的最小正周期为12，‎ 则＝12，得ω＝.‎ 由f(x)的最大值为2，得＝2，‎ 又a>0，所以a＝1.‎ 于是所求函数的解析式为 f(x)＝sinx＋cosx＝2sin，‎ 令x＋＝＋kπ(k∈Z)，‎ 解得x＝1＋6k(k∈Z)，‎ 即函数f(x)图象的对称轴方程为x＝1＋6k(k∈Z)．‎ 易错起源1、　三角函数的概念、诱导公式及同角关系式 例1、(1)点P从(1,0)出发，沿单位圆x2＋y2＝1逆时针方向运动弧长到达Q点，则Q点的坐标为(　　)‎ A．(－，) B．(－，－)‎ C．(－，－) D．(－，)‎ ‎(2)已知sinα＋2cosα＝0，则2sinαcosα－cos2α的值是________．‎ 答案　(1)A　(2)－1‎ 解析　(1)设Q点的坐标为(x，y)，‎ 则x＝cos＝－，y＝sin＝.‎ ‎∴Q点的坐标为(－，)．‎ ‎(2)∵sinα＋2cosα＝0，∴sinα＝－2cosα，‎ ‎∴tanα＝－2，‎ 又∵2sinαcosα－cos2α＝ ‎＝，∴原式＝＝－1.‎ ‎【变式探究】(1)已知点P落在角θ的终边上，且θ∈0,2π)，则θ的值为(　　)‎ A.B.C.D. ‎(2)如图，以Ox为始边作角α (0<α<π)，终边与单位圆相交于点P，已知点P的坐标为，则＝________.‎ 答案　(1)D　(2) 解析　(1)tanθ＝＝＝－1，‎ 又sin>0，cos<0，‎ 所以θ为第四象限角且θ∈0,2π)，所以θ＝.‎ ‎(2)由三角函数定义，‎ 得cosα＝－，sinα＝，‎ ‎∴原式＝＝ ‎＝2cos2α＝2×2＝.‎ ‎【名师点睛】‎ ‎(1)涉及与圆及角有关的函数建模问题(如钟表、摩天轮、水车等)，常常借助三角函数的定义求解．应用定义时，注意三角函数值仅与终边位置有关，与终边上点的位置无关．‎ ‎(2)应用诱导公式时要弄清三角函数在各个象限内的符号；利用同角三角函数的关系化简过程要遵循一定的原则，如切化弦、化异为同、化高为低、化繁为简等．‎ ‎【锦囊妙计，战胜自我】‎ ‎1．三角函数：设α是一个任意角，它的终边与单位圆交于点P(x，y)，则sinα＝y，cosα＝x，tanα＝.各象限角的三角函数值的符号：一全正，二正弦，三正切，四余弦．‎ ‎2．同角关系：sin2α＋cos2α＝1，＝tanα.‎ ‎3．诱导公式：在＋α，k∈Z的诱导公式中“奇变偶不变，符号看象限”．‎ 易错起源2、三角函数的图象及应用 例2、(1)要得到函数y＝sin的图象，只需将函数y＝sin4x的图象(　　)‎ A．向左平移个单位 B．向右平移个单位 C．向左平移个单位 D．向右平移个单位 ‎(2)函数f(x)＝Asin(ωx＋φ)(A，ω，φ为常数，A>0，ω>0，0<φ<π)的图象如图所示，则f()的值为________．‎ 答案　(1)B　(2)1‎ 解析　(1)∵y＝sin＝sin，‎ ‎∴要得到y＝sin的图象，只需将函数y＝sin4x的图象向右平移个单位．‎ ‎(2)根据图象可知，A＝2，＝－，所以周期T＝π，由ω＝＝2.‎ 又函数过点(，2)，‎ 所以有sin(2×＋φ)＝1，而0<φ<π，‎ 所以φ＝，则f(x)＝2sin(2x＋)，‎ 因此f()＝2sin(＋)＝1.‎ ‎【变式探究】(1)已知函数f(x)＝sin(x∈R，ω>0)的最小正周期为π，为了得到函数g(x)＝cosωx的图象，只要将y＝f(x)的图象(　　)‎ A．向左平移个单位长度 B．向右平移个单位长度 C．向左平移个单位长度 D．向右平移个单位长度 ‎(2)如图，某港口一天6时到18时的水深变化曲线近似满足函数y＝3sin＋k，据此函数可知，这段时间水深(单位：m)的最大值为(　　)‎ A．5 B．6‎ C．8 D．10‎ 答案　(1)A　(2)C ‎【名师点睛】‎ ‎(1)已知函数y＝Asin(ωx＋φ)(A>0，ω>0)的图象求解析式时，常采用待定系数法，由图中的最高点、最低点或特殊点求A；由函数的周期确定ω；确定φ常根据“五点法”中的五个点求解，其中一般把第一个零点作为突破口，可以从图象的升降找准第一个零点的位置．‎ ‎(2)在图象变换过程中务必分清是先相位变换，还是先周期变换．变换只是相对于其中的自变量x而言的，如果x的系数不是1，就要把这个系数提取后再确定变换的单位长度和方向．‎ ‎【锦囊妙计，战胜自我】‎ 函数y＝Asin (ωx＋φ)的图象 ‎(1)“五点法”作图：‎ 设z＝ωx＋φ，令z＝0，，π，，2π，求出x的值与相应的y的值，描点、连线可得．‎ ‎(2)图象变换：‎ y＝sinxy＝sin(x＋φ)‎ y＝Asin(ωx＋φ)．‎ 易错起源3、　三角函数的性质 例3、已知函数f(x)＝sinsinx－cos2x.‎ ‎(1)求f(x)的最小正周期和最大值；‎ ‎(2)讨论f(x)在上的单调性．‎ 解　(1)f(x)＝sinsinx－cos2x ‎＝cosxsinx－(1＋cos2x)＝sin2x－cos2x－＝sin－，‎ 因此f(x)的最小正周期为π，最大值为.‎ ‎(2)当x∈时，0≤2x－≤π，从而 当0≤2x－≤，即≤x≤时，f(x)单调递增，‎ 当≤2x－≤π，即≤x≤时，f(x)单调递减．‎ 综上可知，f(x)在上单调递增；在上单调递减．‎ ‎【变式探究】设函数f(x)＝2cos2x＋sin2x＋a(a∈R)．‎ ‎(1)求函数f(x)的最小正周期和单调递增区间；‎ ‎(2)当x∈0，]时，f(x)的最大值为2，求a的值，并求出y＝f(x)(x∈R)的对称轴方程．‎ 解　(1)f(x)＝2cos2x＋sin2x＋a＝1＋cos2x＋sin2x＋a＝sin(2x＋)＋1＋a，‎ 则f(x)的最小正周期T＝＝π，‎ 且当2kπ－≤2x＋≤2kπ＋(k∈Z)，‎ 即kπ－≤x≤kπ＋(k∈Z)时，f(x)单调递增．‎ 所以kπ－，kπ＋](k∈Z)为f(x)的单调递增区间．‎ ‎【名师点睛】‎ 函数y＝Asin(ωx＋φ)的性质及应用的求解思路 第一步：先借助三角恒等变换及相应三角函数公式把待求函数化成y＝Asin(ωx＋φ)＋B的形式；‎ 第二步：把“ωx＋φ”视为一个整体，借助复合函数性质求y＝Asin(ωx＋φ)＋B的单调性及奇偶性、最值、对称性等问题．‎ ‎【锦囊妙计，战胜自我】‎ ‎1．三角函数的单调区间：‎ y＝sinx的单调递增区间是2kπ－，2kπ＋](k∈Z)，单调递减区间是2kπ＋，2kπ＋](k∈Z)；‎ y＝cosx的单调递增区间是2kπ－π，2kπ](k∈Z)，单调递减区间是2kπ，2kπ＋π](k∈Z)；‎ y＝tanx的递增区间是(kπ－，kπ＋)(k∈Z)．‎ ‎2．y＝Asin(ωx＋φ)，当φ＝kπ(k∈Z)时为奇函数；‎ 当φ＝kπ＋(k∈Z)时为偶函数；对称轴方程可由ωx＋φ＝kπ＋(k∈Z)求得．‎ y＝Acos(ωx＋φ)，当φ＝kπ＋(k∈Z)时为奇函数；‎ 当φ＝kπ(k∈Z)时为偶函数；对称轴方程可由ωx＋φ＝kπ(k∈Z)求得．‎ y＝Atan(ωx＋φ)，当φ＝kπ(k∈Z)时为奇函数．‎ ‎1．若0≤sinα≤，且α∈－2π，0]，则α的取值范围是(　　)‎ A.∪ B.∪(k∈Z)‎ C.∪ D.∪(k∈Z)‎ 答案　A 解析　根据题意并结合正弦线可知，‎ α满足∪(k∈Z)，‎ ‎∵α∈－2π，0]，‎ ‎∴α的取值范围是∪.‎ 故选A.‎ ‎2．函数f(x)＝cos的图象向左平移个单位长度后得到的图象对应的函数为(　　)‎ A．y＝cos B．y＝sin C．y＝cos D．y＝sin 答案　C 解析　函数f(x)＝cos的图象向左平移个单位长度后所得图象的解析式为y＝cos3(x＋)－]＝cos(3x＋)，故选C.‎ ‎3．已知tanα＝3，则的值为(　　)‎ A．－ B．－3‎ C. D．3‎ 答案　A 解析　＝＝－＝－.‎ ‎4．已知角α的终边经过点A(－，a)，若点A在抛物线y＝－x2的准线上，则sinα等于(　　)‎ A．－ B. C．－ D. 答案　D 解析　由条件，得抛物线的准线方程为y＝1，因为点A(－，a)在抛物线y＝－x2的准线上，所以a＝1，所以点A(－，1)，所以sinα＝＝.‎ ‎5.函数f(x)＝Asinωx(A>0，ω>0)的部分图象如图所示，则f(1)＋f(2)＋f(3)＋…＋f(2015)的值为(　　)‎ A．0　　　　 B．3 C．6　　　　 D．－ 答案　A 解析　由图可得，A＝2，T＝8，＝8，ω＝，‎ ‎∴f(x)＝2sinx，‎ ‎∴f(1)＝，f(2)＝2，f(3)＝，f(4)＝0，f(5)＝－，‎ f(6)＝－2，f(7)＝－，f(8)＝0，而2015＝8×251＋7，‎ ‎∴f(1)＋f(2)＋…＋f(2015)＝0.‎ ‎6．函数y＝2sin(－)(0≤x≤9)的最大值与最小值之差为________．‎ 答案　2＋ ‎7．已知函数f(x)＝3sin(ωx－)(ω>0)和g(x)＝3cos(2x＋φ)的图象的对称中心完全相同，若x∈0，]，则f(x)的取值范围是________．‎ 答案　－，3]‎ 解析　由两个三角函数图象的对称中心完全相同，可知两函数的周期相同，故ω＝2，所以f(x)＝3sin(2x－)，那么当x∈0，]时，－≤2x－≤，‎ 所以－≤sin(2x－)≤1，故f(x)∈－，3]．‎ ‎8．已知α是三角形的内角，若sinα＋cosα＝，则tanα＝________.‎ 答案　－ 解析　方法一　由 解得或 因为α∈(0，π)，所以sinα>0，‎ 所以所以tanα＝＝－.‎ 方法二　由已知得(sinα＋cosα)2＝，‎ 化简得2sinαcosα＝－，‎ 则可知角α是第二象限角，‎ 且(sinα－cosα)2＝1－2sinαcosα＝，‎ 由于sinα－cosα>0，所以sinα－cosα＝，‎ 将该式与sinα＋cosα＝联立，‎ 解得所以tanα＝＝－.‎ ‎9．已知函数f(x)＝cos.‎ ‎(1)若f(α)＝，其中<α<，求sin的值；‎ ‎(2)设g(x)＝f(x)·f，求函数g(x)在区间上的最大值和最小值．‎ 解　(1)因为f(α)＝cos＝，‎ 且0<α－<，‎ 所以sin＝.‎ ‎(2)g(x)＝f(x)·f ‎＝cos·cos ‎＝sin·cos＝cos2x.‎ x∈时，2x∈.‎ 则当x＝0时，g(x)的最大值为；‎ 当x＝时，g(x)的最小值为－.‎ ‎10．已知a>0，函数f(x)＝－2asin＋2a＋b，当x∈时，－5≤f(x)≤1.‎ ‎(1)求常数a，b的值；‎ ‎(2)设g(x)＝f且lgg(x)>0，求g(x)的单调区间．‎ 解　(1)∵x∈，∴2x＋∈.‎ ‎∴sin∈，‎ ‎∴－2asin∈－2a，a]．‎ ‎∴f(x)∈b,3a＋b]，又∵－5≤f(x)≤1，‎ ‎∴b＝－5,3a＋b＝1，因此a＝2，b＝－5.‎ ‎(2)由(1)得，f(x)＝－4sin－1，‎ g(x)＝f＝－4sin－1‎ ‎＝4sin－1，‎ 又由lgg(x)>0，得g(x)>1，‎ ‎∴4sin－1>1，∴sin>，‎ ‎∴2kπ＋<2x＋<2kπ＋，k∈Z，‎ 其中当2kπ＋<2x＋≤2kπ＋，k∈Z时，‎ g(x)单调递增，即kπ0)的部分图象如图所示，点A，B是最高点，点C是最低点，若△ABC是直角三角形，则f()＝________.‎ 答案　 ‎12．已知函数f(x)＝Asin(ωx＋)(A>0，ω>0)，g(x)＝tanx，它们的最小正周期之积为2π2，f(x)的最大值为2g()．‎ ‎(1)求f(x)的单调递增区间；‎ ‎(2)设h(x)＝f2(x)＋2cos2x.当x∈a，)时，h(x)有最小值为3，求a的值．‎ 解　(1)由题意，得·π＝2π2，所以ω＝1.‎ 又A＝2g()＝2tanπ＝2tan＝2，‎ 所以f(x)＝2sin(x＋)．‎ 令2kπ－≤x＋≤2kπ＋(k∈Z)，‎ 得2kπ－≤x≤2kπ＋(k∈Z)．‎ 故f(x)的单调递增区间为2kπ－，2kπ＋](k∈Z)．‎ ‎(2)因为h(x)＝f2(x)＋2cos2x ‎＝×4×sin2(x＋)＋2cos2x ‎＝3(sinx＋cosx)2＋2cos2x ‎＝3＋3sin2x＋(cos2x＋1)‎ ‎＝3＋＋2sin(2x＋)，‎ 又h(x)有最小值为3，‎ 所以有3＋＋2sin(2x＋)＝3，‎ 即sin(2x＋)＝－.‎ 因为x∈a，)，所以2x＋∈2a＋，)，‎ 所以2a＋＝－，即a＝－.‎