2021届北师大版高考理科数一轮复习教师用书：第二章　第6讲　对数与对数函数 14页

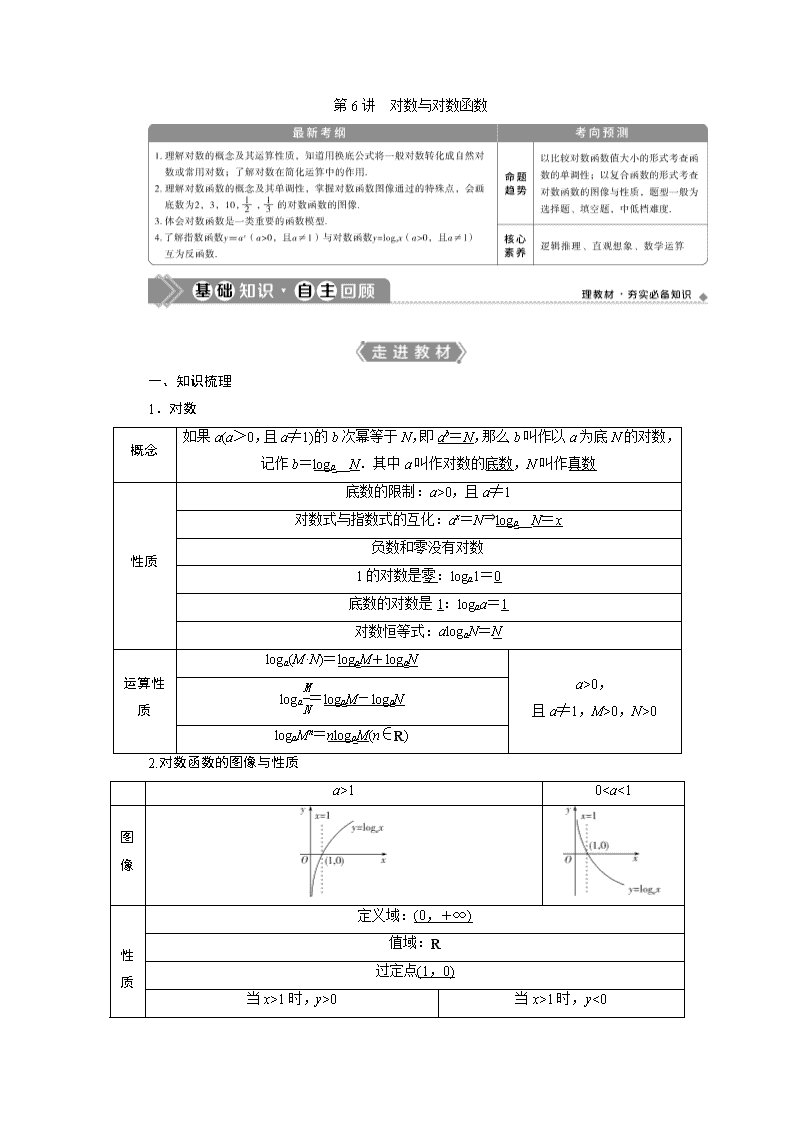
第6讲　对数与对数函数 ‎　‎ 一、知识梳理 ‎1．对数 概念 如果a(a＞0，且a≠1)的b次幂等于N，即ab＝N，那么b叫作以a为底N的对数，记作b＝loga__N．其中a叫作对数的底数，N叫作真数 性质 底数的限制：a>0，且a≠1‎ 对数式与指数式的互化：ax＝N⇒loga__N＝x 负数和零没有对数 ‎1的对数是零：loga1＝0‎ 底数的对数是1：logaa＝1‎ 对数恒等式：alogaN＝N 运算性质 loga(M·N)＝logaM＋logaN a>0，‎ 且a≠1，M>0，N>0‎ loga＝logaM－logaN logaMn＝nlogaM(n∈R)‎ ‎2.对数函数的图像与性质 a>1‎ ‎01时，y>0‎ 当x>1时，y<0‎ 当00‎ 在(0，＋∞)上是增函数 在(0，＋∞)上是减函数 ‎3.反函数 指数函数y＝ax与对数函数y＝logax互为反函数，它们的图象关于直线y＝x对称．‎ 常用结论 ‎1．换底公式的三个重要结论 ‎①logab＝；‎ ‎②logambn＝logab；‎ ‎③logab·logbc·logcd＝logad.‎ ‎2．对数函数的图象与底数大小的关系 如图，作直线y＝1，则该直线与四个函数图象交点的横坐标为相应的底数．‎ 故01.所以c>a>b.‎ 答案：c>a>b 一、思考辨析 判断正误(正确的打“√”，错误的打“×”)‎ ‎(1)loga(MN)＝logaM＋logaN.(　　)‎ ‎(2)logax·logay＝loga(x＋y)．(　　)‎ ‎(3)函数y＝log2x及y＝log3x都是对数函数．(　　)‎ ‎(4)对数函数y＝logax(a>0且a≠1)在(0，＋∞)上是增函数．(　　)‎ ‎(5)函数y＝ln 与y＝ln(1＋x)－ln(1－x)的定义域相同．(　　)‎ ‎(6)对数函数y＝logax(a>0且a≠1)的图象过定点(1，0)，且过点(a，1)，，函数图象只经过第一、四象限．(　　)‎ 答案：(1)×　(2)×　(3)×　(4)×　(5)√　(6)√‎ 二、易错纠偏 (1)对数函数图象的特征不熟致误；‎ ‎(2)忽视对底数的讨论致误；‎ ‎(3)忽视对数函数的定义域致误．‎ ‎1．已知a>0，a≠1，函数y＝ax与y＝loga(－x)的图象可能是________．(填序号)‎ 解析：函数y＝loga(－x)的图象与y＝logax的图象关于y轴对称，符合条件的只有②.‎ 答案：②‎ ‎2．函数y＝logax(a>0，a≠1)在[2，4]上的最大值与最小值的差是1，则a＝________．‎ 解析：分两种情况讨论：①当a>1时，有loga4－loga2＝1，解得a＝2；②当00，y>0，2x－3y>0，‎ 所以＝，所以log＝2.‎ 答案：2‎ ‎3．设2a＝5b＝m，且＋＝2，则m等于________．‎ 解析：由2a＝5b＝m得a＝log2m，b＝log5m，‎ 所以＋＝logm2＋logm5＝logm10.‎ 因为＋＝2，所以logm10＝2.‎ 所以m2＝10，所以m＝.‎ 答案： ‎4．已知log23＝a，3b＝7，则log32的值为________．‎ 解析：由题意3b＝7，所以log37＝b.‎ 所以log32＝log＝＝＝＝.‎ 答案： 对数运算的一般思路 ‎(1)拆：首先利用幂的运算把底数或真数进行变形，化成分数指数幂的形式，使幂的底数最简，然后利用对数运算性质化简合并．‎ ‎(2)合：将对数式化为同底数对数的和、差、倍数运算，然后逆用对数的运算性质，转化为同底对数真数的积、商、幂的运算．　 ‎ ‎　　　　　　对数函数的图象及应用(师生共研)‎ ‎ (1)(2019·高考浙江卷)在同一直角坐标系中，函数y＝，y＝loga(a>0，且a≠1)的图象可能是(　　)‎ ‎(2)已知函数f(x)＝，若存在实数a，b，c，d，满足f(a)＝f(b)＝f(c)＝f(d)，其中d＞c＞b＞a＞0，则abcd的取值范围________．‎ ‎【解析】　(1)对于函数y＝loga，当y＝0时，有x＋＝1，得x＝，即y＝loga的图象恒过定点，排除选项A、C；函数y＝与y＝loga在各自定义域上单调性相反，排除选项B，故选D.‎ ‎(2)‎ 由题意可得－log3a＝log3b＝c2－c＋8＝d2－d＋8，‎ 可得log3(ab)＝0，故ab＝1.‎ 结合函数f(x)的图象，在区间[3，＋∞)上，‎ 令f(x)＝1可得c＝3、d＝7、cd＝21.‎ 令f(x)＝0可得c＝4、d＝6、cd＝24.‎ 故有21＜abcd＜24.‎ ‎【答案】　(1)D　(2)(21，24) ‎ 对数函数图象的识别及应用方法 ‎(1)在识别函数图象时，要善于利用已知函数的性质、函数图象上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项．‎ ‎(2)一些对数型方程、不等式问题常转化为相应的函数图象问题，利用数形结合法求解．　 ‎ ‎1.已知函数y＝loga(x＋c)(a，c为常数，其中a>0，a≠1)的图象如图，则下列结论成立的是(　　) ‎ A．a>1，c>1‎ B．a>1，01‎ D．01.‎ 答案：(1，＋∞)‎ ‎　　　　　　对数函数的性质及应用(多维探究)‎ 角度一　比较大小 ‎ 已知a＝log2e，b＝ln 2，c＝log，则a，b，c的大小关系为(　　)‎ A．a>b>c　　　　　　　 B．b>a>c C．c>b>a D．c>a>b ‎【解析】　因为c＝log＝log23>log2e＝a，所以c>a.‎ 因为b＝ln 2＝<1b.‎ 所以c>a>b.‎ ‎【答案】　D 比较对数值大小的常见类型及解题方法 常见类型 解题方法 底数为同一常数 可由对数函数的单调性直接进行判断 底数为同一字母 需对底数进行分类讨论 底数不同，真数相同 可以先用换底公式化为同底后，再进行比较 底数与真数都不同 常借助1，0等中间量进行比较 角度二　解简单对数不等式 ‎ 已知不等式logx(2x2＋1)logab 借助y＝logax的单调性求解，如果a的取值不确定，需分a ‎>1与0b 需先将b化为以a为底的对数式的形式，再借助y＝logax的单调性求解 ‎[提醒]　注意对数式的真数大于零，且不等于1.　 ‎ 角度三　与对数函数有关的综合问题 ‎ 已知函数f(x)＝loga(3－ax)．‎ ‎(1)当x∈[0，2]时，函数f(x)恒有意义，求实数a的取值范围；‎ ‎(2)是否存在这样的实数a，使得函数f(x)在区间[1，2]上为减函数，并且最大值为1？如果存在，试求出a的值；如果不存在，请说明理由．‎ ‎【解】　(1)因为a>0且a≠1，设t(x)＝3－ax，‎ 则t(x)＝3－ax为减函数，‎ x∈[0，2]时，t(x)的最小值为3－2a，‎ 当x∈[0，2]时，f(x)恒有意义，‎ 即x∈[0，2]时，3－ax>0恒成立．‎ 所以3－2a>0.所以a<.‎ 又a>0且a≠1，所以a∈(0，1)∪.‎ ‎(2)t(x)＝3－ax，因为a>0，‎ 所以函数t(x)为减函数．‎ 因为f(x)在区间[1，2]上为减函数，‎ 所以y＝logat为增函数，‎ 所以a>1，当x∈[1，2]时，t(x)最小值为3－2a，f(x)最大值为f(1)＝loga(3－a)，‎ 所以即 故不存在这样的实数a，使得函数f(x)在区间[1，2]上为减函数，并且最大值为1.‎ 解决与对数函数有关的函数的单调性问题的步骤 ‎　 ‎ ‎1．(2019·高考天津卷)已知a＝log52，b＝log0.50.2，c＝0.50.2，则a，b，c的大小关系为 ‎(　　)‎ A．a0.51＝，故alog0.50.25＝2，而c＝0.50.2<0.50＝1，故c0，则实数a的取值范围是(　　)‎ A. B． C. D．(0，＋∞)‎ 解析：选A.因为－10，所以0<2a<1，所以00，若函数f(x)＝log3(ax2－x)在[3，4]上是增函数，则a的取值范围是________．‎ 解析：要使f(x)＝log3(ax2－x)在[3，4]上递增，‎ 则y＝ax2－x在[3，4]上递增，‎ 且y＝ax2－x>0恒成立，‎ 即解得a>.‎ 答案： ‎　数形结合法在对数函数问题中的应用 ‎ 设方程10x＝|lg(－x)|的两个根分别为x1，x2，则(　　)‎ A．x1x2<0　　　　　　 B．x1x2＝0‎ C．x1x2>1 D．01.5，c＝ln 2<1，所以cy>1.‎ ‎4．函数f(x)＝|loga(x＋1)|(a>0，且a≠1)的大致图象是(　　)‎ 解析：选C.函数f(x)＝|loga(x＋1)|的定义域为{x|x>－1}，且对任意的x，均有f(x)≥0，结合对数函数的图象可知选C.‎ ‎5．若函数y＝loga(x2－ax＋1)有最小值，则a的取值范围是　(　　)‎ A．01时，y有最小值，则说明x2－ax＋1有最小值，故x2－ax＋1＝0中Δ<0，即a2－4<0，所以2>a>1.‎ 当00，故A＝＝7.‎ 答案：7 ‎8．已知函数f(x)＝|log3 x|，实数m，n满足02，不满足题意．综上可得＝9.‎ 答案：9‎ ‎9．设f(x)＝loga(1＋x)＋loga(3－x)(a>0，且a≠1)，且f(1)＝2.‎ ‎(1)求a的值及f(x)的定义域；‎ ‎(2)求f(x)在区间上的最大值．‎ 解：(1)因为f(1)＝2，所以loga4＝2(a>0，且a≠1)，所以a＝2.‎ 由得－11，而x1＝log2<0，0x2>x1.故选A.‎ ‎3．已知函数f(x)＝log0.5(x2－ax＋3a)在[2，＋∞)上是减少的，则a的取值范围为________．‎ 解析：令g(x)＝x2－ax＋3a，‎ 因为f(x)＝log0.5(x2－ax＋3a)在[2，＋∞) 是减少的，‎ 所以函数g(x)在区间[2，＋∞)内是增加的，且恒大于0，‎ 所以a≤2且g(2)＞0，‎ 所以a≤4且4＋a＞0，所以－4＜a≤4.‎ 答案：(－4，4]‎ ‎4．设函数f(x)＝|logax|(00时，f(x)＝logx.‎ ‎(1)求函数f(x)的解析式；‎ ‎(2)解不等式f(x2－1)>－2.‎ 解：(1)当x<0时，－x>0，则f(－x)＝log(－x)．‎ 因为函数f(x)是偶函数，‎ 所以f(－x)＝f(x)＝log(－x)，‎ 所以函数f(x)的解析式为f(x)＝ ‎(2)因为f(4)＝log4＝－2，f(x)是偶函数，‎ 所以不等式f(x2－1)>－2转化为f(|x2－1|)>f(4)．‎ 又因为函数f(x)在(0，＋∞)上是减函数，‎ 所以|x2－1|<4，解得－