数学理卷·2018届重庆市巴蜀中学高三上学期第五次月考（2017 13页

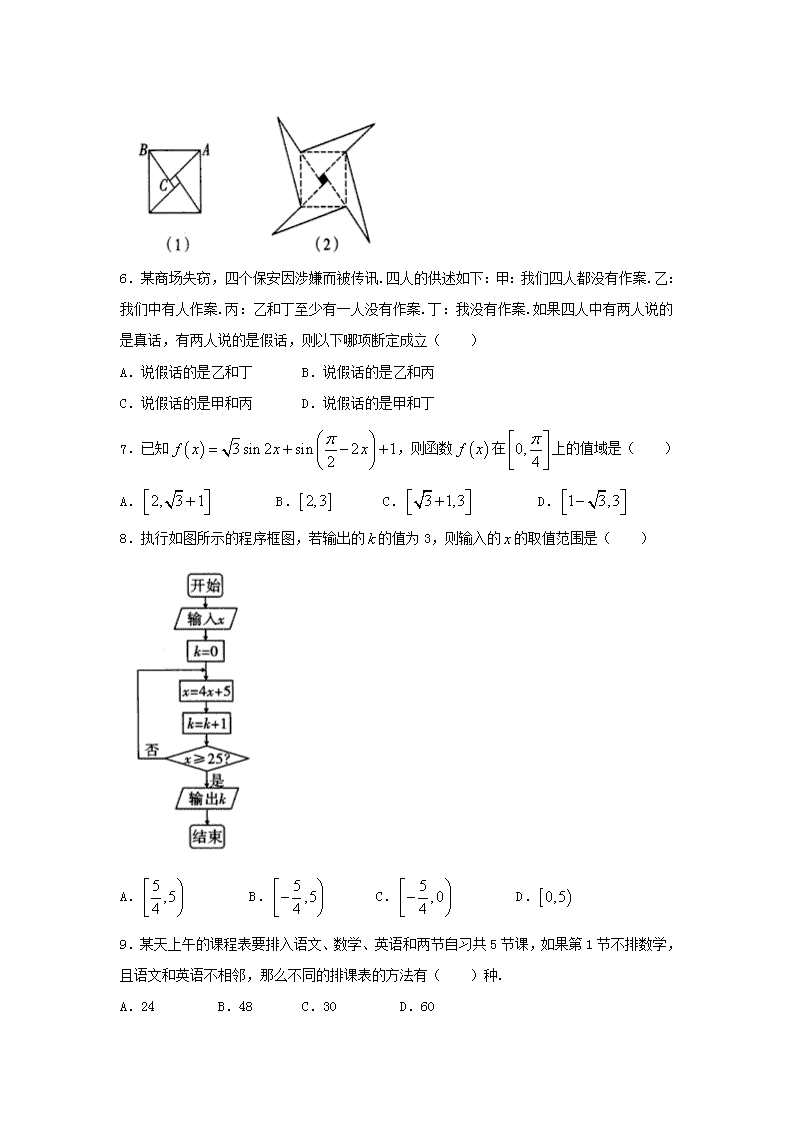
巴蜀中学2018届高考适应性月考卷（五）‎ 理科数学 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合，，则（ ）‎ A． B． C． D．‎ ‎2．设，则（ ）‎ A． B． C． D．2‎ ‎3．平面向量满足，，，则向量与的夹角为（ ）‎ A． B． C． D．‎ ‎4．已知双曲线的一条渐近线与直线平行，则双曲线的离心率等于（ ）‎ A． B． C． D．‎ ‎5．我国汉代数学家赵爽为了证明勾股定理，创制了一幅弦图，后人称其为“赵爽弦图”.弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图（1））.若直角三角形的两条直角边，将四个直角三角形中较长的直角边分别向外延长一倍，得到图（2）所示的“数学风车”，在该“数学风车”内随机取一点，则此点取自黑色部分的概率是（ ）‎ A． B． C． D．‎ ‎6．某商场失窃，四个保安因涉嫌而被传讯.四人的供述如下：甲：我们四人都没有作案.乙：我们中有人作案.丙：乙和丁至少有一人没有作案.丁：我没有作案.如果四人中有两人说的是真话，有两人说的是假话，则以下哪项断定成立（ ）‎ A．说假话的是乙和丁 B．说假话的是乙和丙 C．说假话的是甲和丙 D．说假话的是甲和丁 ‎7．已知，则函数在上的值域是（ ）‎ A． B． C． D．‎ ‎8．执行如图所示的程序框图，若输出的的值为3，则输入的的取值范围是（ ）‎ A． B． C． D．‎ ‎9．某天上午的课程表要排入语文、数学、英语和两节自习共5节课，如果第1节不排数学，且语文和英语不相邻，那么不同的排课表的方法有（ ）种.‎ A．24 B．48 C．30 D．60‎ ‎10．已知是上的偶函数，且在上单调递减，设，，，下列结论正确的是（ ）‎ A． B． C． D．‎ ‎11．设直线与抛物线相交于两点，与圆相切于点，且为线段的中点，若这样的直线恰有2条，则的取值范围是（ ）‎ A． B． C． D．‎ ‎12．已知函数，过点作函数的两条切线，切点分别为，下列关于直线斜率的正负，说法正确的是（ ）‎ A． B． C． D．不确定 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．二项式展开式中的常数项是 ．‎ ‎14．设数列的前项和为，若，则 ．‎ ‎15．设实数满足约束条件的最小值是 ．‎ ‎16．在四边形中，，，，则四边形的面积的最大值是 ．‎ 三、解答题 （本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．） ‎ ‎17．在等差数列中，设前项和为，满足且，在数列中，满足，且数列为等比数列.‎ ‎（Ⅰ）求与；‎ ‎（Ⅱ）求数列的前项和.‎ ‎18．如图，在正三棱柱中，所有棱长均为2，设交于点，点 为线段的中点.‎ ‎（Ⅰ）证明：；‎ ‎（Ⅱ）求二面角的余弦值.‎ ‎19．作为加班拍档、创业伴侣、春运神器，曾几何时，方便面是我们生活中重要的“朋友”，然而这种景象却在近5年出现了戏剧性的逆转。统计显示，2011年之前，方便面销量在中国连续18年保持两位数增长，2013年的年销量更是创下462亿包的辉煌战绩；但2013年以来，方便面销量却连续3年下跌，只剩385亿包，具体如下表.相较于方便面，络订餐成为大家更加青睐的消费选择.近年来，络订餐市场规模的“井喷式”增长，也充分反映了人们消费方式的变化.‎ ‎（Ⅰ）根据上表，求关于的线性回归方程，用所求回归方程预测2017年（）方便面在中国的年销量；‎ ‎（Ⅱ）方便面销量遭遇滑铁卢受到哪些因素影响？中国的消费业态发生了怎样的转变？某媒体记者随机对身边的10位朋友做了一次调查，其中5位受访者表示超过1年未吃过方便面；3位受访者认为方便面是健康食品；而9位受访者有过络订餐的经历.现从这10人中抽取3人进行深度访谈，记表示随机抽取的3人认为方便面是健康食品的人数，求随机变量的分布列及数学期望.‎ 参考公式：‎ 回归方程：，其中，‎ 参考数据：.‎ ‎20．已知椭圆短轴的两个顶点与右焦点的连线构成等边三角形，过点且垂直于轴的直线被椭圆截得的线段长为1.‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）如图，过点的直线交椭圆于两点，再过点作斜率为的直线交椭圆于点，问直线与直线的交点是否为定点？若是，求出这个定点；若不是，请说明理由.‎ ‎21．已知函数.‎ ‎（Ⅰ）若和2是函数的两个极值点，求曲线在点处的切线方程；‎ ‎（Ⅱ）若，则方程在内有解，求的取值范围.‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．‎ ‎22．选修4-4：坐标系与参数方程 已知在直角坐标系中，曲线的方程为，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，直线与交于两点，与交于两点.‎ ‎（Ⅰ）若，求的面积；‎ ‎（Ⅱ）求的最小值.‎ ‎23．选修4-5：不等式选讲 已知函数的最小值为.‎ ‎（Ⅰ）求实数的值；‎ ‎（Ⅱ）在（Ⅰ）的条件下，正实数满足，求证：.‎ 巴蜀中学2018届高考适应性月考卷（五）‎ 理科数学参考答案 一、选择题 ‎1-5:BBCAC 6-10:DBCCC 11、12：DA 二、填空题 ‎13．5 14．31 15． 16．‎ 三、解答题 ‎17．解：（Ⅰ）因为在等差数列中，，，‎ 所以解得 所以.‎ 又∵，，‎ ‎∴数列是首项为1，公比为3的等比数列，‎ ‎∴.‎ ‎（Ⅱ）由（Ⅰ）知，，‎ ‎∴，‎ ‎，‎ ‎∴‎ ‎，‎ ‎∴.‎ ‎18．（Ⅰ）证明：如图，连接，‎ 则由点为线段的中点可知，‎ 故为等腰三角形，‎ 而为底边的中点，故，‎ 由于正三棱柱的所有棱长都相等，‎ 故四边形为正方形，故，‎ 因为，，‎ 所以平面，所以.‎ ‎（Ⅱ）解：以点为原点，直线为坐标轴建立如图所示的空间坐标系，‎ 此时，，，，‎ ‎，，‎ 设平面的法向量为，‎ 由可得：‎ 可取，，，‎ 故，‎ 同理，平面的法向量为，‎ ‎.‎ ‎19．解：（Ⅰ），，，，‎ ‎，‎ 所以，‎ 当时，.‎ ‎（Ⅱ）依题意，10人中认为方便面是健康食品的有3人，的可能值为0,1,2,3，‎ 所以，，，‎ ‎，，‎ ‎.‎ ‎20．解：（Ⅰ）由题意得解得，，‎ 所以椭圆的方程为：.‎ ‎（Ⅱ）直线的斜率显然存在，不妨设直线的方程为，‎ 即，‎ 联立方程得，‎ 设，，，‎ 当时，，，‎ 则的方程为，①‎ 与椭圆联立得，‎ 则，所以，‎ 代入①得.‎ 直线的方程为：，联立，‎ ‎.‎ ‎，‎ ‎，‎ 所以，，直线与直线交于定点.‎ ‎21．解：（Ⅰ），‎ 由题意，解得 此时，，‎ ‎，，‎ 切点为，所以切线方程.‎ ‎（Ⅱ），，①‎ ‎，，‎ 令，则在内有零点.‎ 设为在内的一个零点，则由，知 在区间和上不可能单调递增，也不可能单调递减.‎ 设，则在区间和上均存在零点，‎ 即在上至少有两个零点，‎ ‎，，‎ 当时，，在区间上递增，不可能有两个及以上零点；‎ 当时，，在区间上递减，不可能有两个及以上零点；‎ 当时，令，得，‎ ‎∴在区间上递减，‎ 在上递增，在区间上存在最小值，‎ 若有两个零点，则有，，，‎ ‎.‎ 设，，则，‎ 令，得，‎ 当时，，递增，‎ 当时，，递减，‎ ‎，‎ ‎∴恒成立，‎ 由，，‎ 得，‎ 当时，设的两个零点为，‎ 则在上递增，在上递减，在上递增，‎ ‎∴，‎ ‎，所以在内有零点，‎ 综上，实数的取值范围是.‎ ‎22．解：（Ⅰ）将的方程化为普通方程得，‎ 时，直线的方程为，‎ 到直线的距离，‎ ‎，.‎ ‎（Ⅱ）的方程分别为，‎ ‎∴原式.‎ ‎∵，‎ ‎∴最小值为，‎ 当，时取到等号.‎ ‎23．解：（Ⅰ）因为 所以当时，函数单调递减，‎ 当时，函数单调递增.‎ 所以当时，实数.‎ ‎（Ⅱ）‎ ‎，‎ 因为正数满足，‎ 所以，，当且仅当时取等号.‎