【数学】2020届一轮复习人教B版 分类加法计数原理和分步乘法计数原理 学案 8页

分类加法计数原理和分步乘法计数原理 ‎ ‎ ‎【学习目标】‎ ‎1．理解分类加法计数原理和分步乘法计数原理．‎ ‎ 2．理解分类加法计数原理和分步乘法计数原理的区别．‎ ‎ 3．会用分类加法计数原理或分步乘法计数原理分析和解决一些简单的实际问题．‎ ‎【要点梳理】‎ 要点一：分类加法计数原理(也称加法原理)‎ ‎1．分类加法计数原理：‎ 完成一件事,有类办法.在第1类办法中有种不同方法,在第2类办法中有种不同的方法,……,在第类办法中有种不同方法,那么完成这件事共有种不同的方法.‎ ‎2．加法原理的特点是：‎ ‎① 完成一件事有若干不同方法，这些方法可以分成n类；‎ ‎② 用每一类中的每一种方法都可以完成这件事；‎ ‎③ 把每一类的方法数相加，就可以得到完成这件事的所有方法数．‎ 要点诠释：‎ 使用分类加法计数原理计算完成某件事的方法数，第一步是对这件事确定一个标准进行分类，第二步是确定各类的方法数，第三步是取和。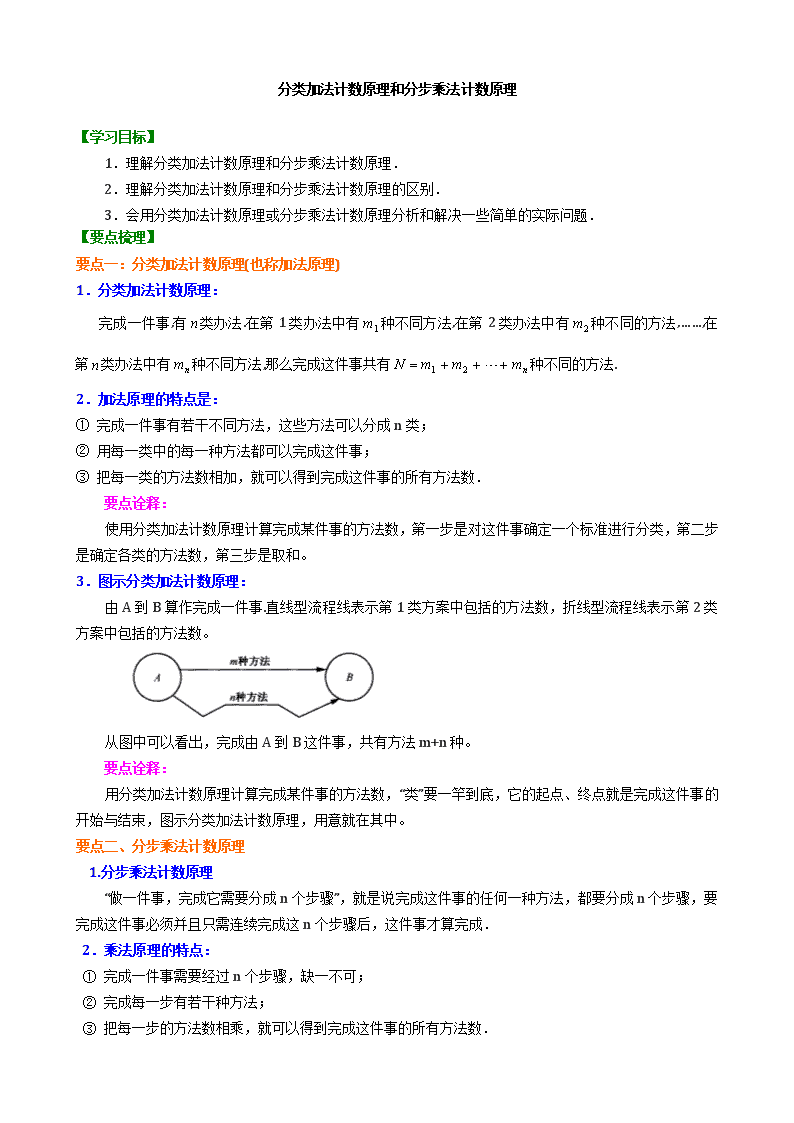‎ ‎3．图示分类加法计数原理：‎ 由A到B算作完成一件事.直线型流程线表示第1类方案中包括的方法数，折线型流程线表示第2类方案中包括的方法数。‎ 从图中可以看出，完成由A到B这件事，共有方法m+n种。‎ 要点诠释：‎ 用分类加法计数原理计算完成某件事的方法数，“类”要一竿到底，它的起点、终点就是完成这件事的开始与结束，图示分类加法计数原理，用意就在其中。‎ 要点二、分步乘法计数原理 ‎1.分步乘法计数原理 ‎ “做一件事，完成它需要分成n个步骤”，就是说完成这件事的任何一种方法，都要分成n个步骤，要完成这件事必须并且只需连续完成这n个步骤后，这件事才算完成．‎ ‎2．乘法原理的特点：‎ ‎① 完成一件事需要经过n个步骤，缺一不可；‎ ‎② 完成每一步有若干种方法；‎ ‎③ 把每一步的方法数相乘，就可以得到完成这件事的所有方法数．‎ 要点诠释：‎ 使用分步乘法计数原理计算完成某件事的方法数，第一步是对完成这件事进行分步，第二步是确定各步的方法数，第三步是求积。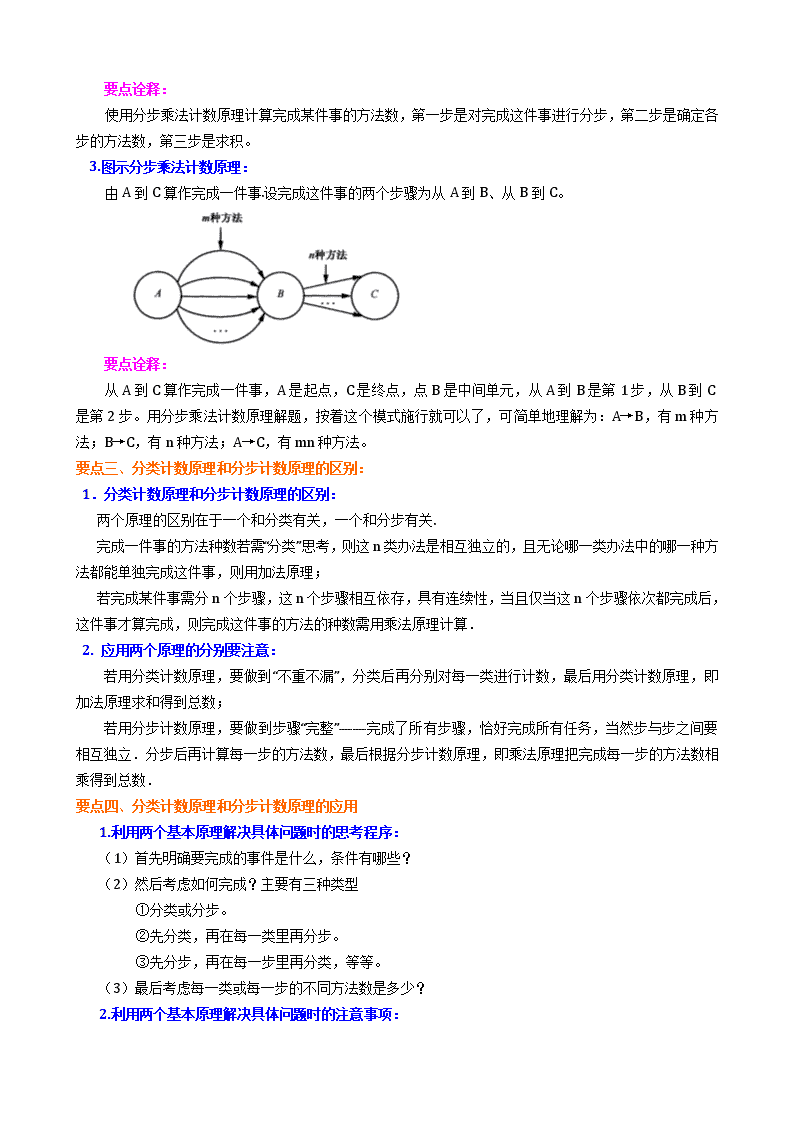‎ ‎3.图示分步乘法计数原理：‎ 由A到C算作完成一件事.设完成这件事的两个步骤为从A到B、从B到C。‎ 要点诠释：‎ 从A到C算作完成一件事，A是起点，C是终点，点B是中间单元，从A到B是第1步，从B到C是第2步。用分步乘法计数原理解题，按着这个模式施行就可以了，可简单地理解为：A→B，有m种方法；B→C，有n种方法；A→C，有mn种方法。‎ 要点三、分类计数原理和分步计数原理的区别：‎ ‎1．分类计数原理和分步计数原理的区别：‎ 两个原理的区别在于一个和分类有关，一个和分步有关.‎ 完成一件事的方法种数若需“分类”思考，则这n类办法是相互独立的，且无论哪一类办法中的哪一种方法都能单独完成这件事，则用加法原理；‎ 若完成某件事需分n个步骤，这n个步骤相互依存，具有连续性，当且仅当这n个步骤依次都完成后，这件事才算完成，则完成这件事的方法的种数需用乘法原理计算．‎ ‎2. 应用两个原理的分别要注意：‎ 若用分类计数原理，要做到“不重不漏”，分类后再分别对每一类进行计数，最后用分类计数原理，即加法原理求和得到总数；‎ 若用分步计数原理，要做到步骤“完整”——完成了所有步骤，恰好完成所有任务，当然步与步之间要相互独立．分步后再计算每一步的方法数，最后根据分步计数原理，即乘法原理把完成每一步的方法数相乘得到总数．‎ 要点四、分类计数原理和分步计数原理的应用 ‎1.利用两个基本原理解决具体问题时的思考程序：‎ ‎（1）首先明确要完成的事件是什么，条件有哪些？‎ ‎（2）然后考虑如何完成？主要有三种类型 ‎①分类或分步。‎ ‎②先分类，再在每一类里再分步。‎ ‎③先分步，再在每一步里再分类，等等。‎ ‎（3）最后考虑每一类或每一步的不同方法数是多少？‎ ‎2.利用两个基本原理解决具体问题时的注意事项：‎ ‎（1）应用分类计数原理，应注意：‎ ‎①分类时，要按一个标准来分，最忌采用双重或多重标准分类；‎ ‎②每一类中的每一种方法都可以独立地完成此任务；它的起点、终点就是完成这件事情的开始和结束；‎ ‎③两类不同办法中的具体方法，互不相同(即分类不重)；‎ ‎④完成此任务的任何一种方法，都属于某一类(即分类不漏).‎ ‎（2）应用分步计数原理，应注意：‎ ‎①任何一步的一种方法都不能完成此任务，必须且只须连续完成这n步才能完成此任务；‎ ‎②各步计数相互独立； ‎ ‎③只要有一步中所采取的方法不同，则对应的完成此事的方法也不同.‎ ‎3.利用两个基本原理解决具体问题时的方法技巧：‎ 利用两个基本原理解决具体问题，关键环节是分类或者分步。类与步的关系式辩证的。有些问题需要先分类，再在每一类里再分步；有些问题需要先分步，再在每一步里再分类，等等。到底采用何种顺序分类与分步，要看类的趋势和步的趋势谁大谁小。下面用用流程图直观描述。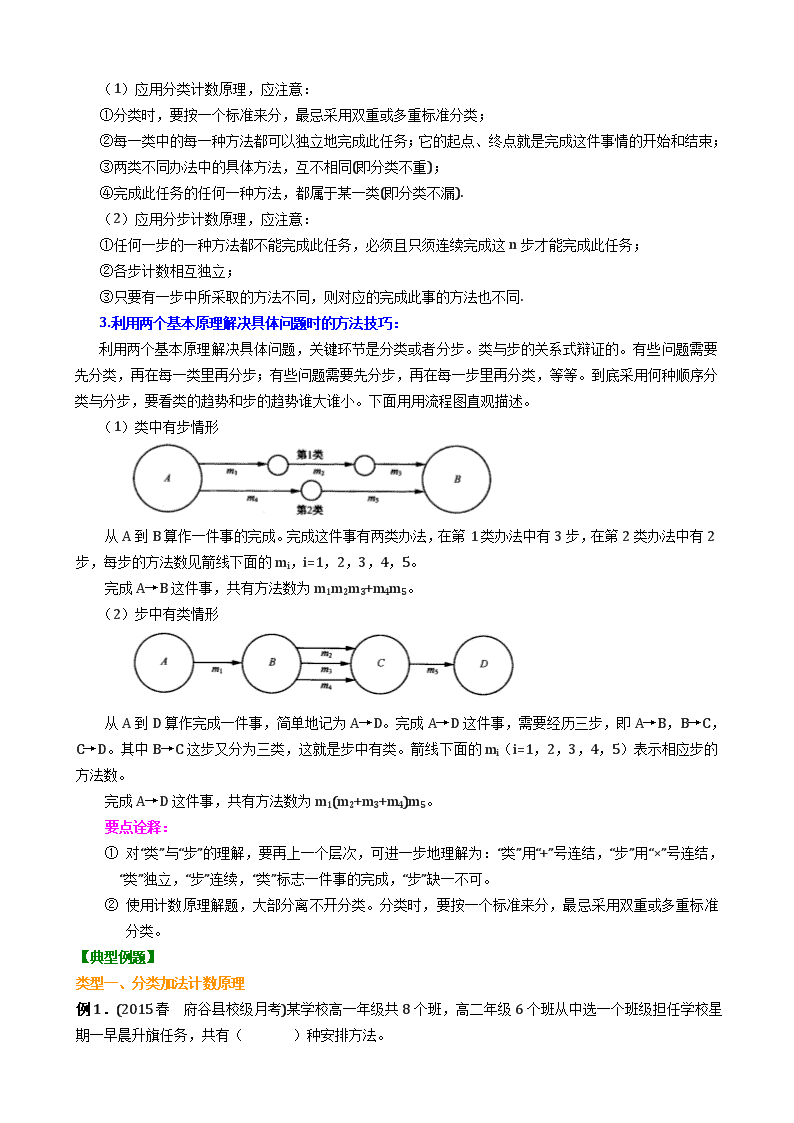‎ ‎（1）类中有步情形 从A到B算作一件事的完成。完成这件事有两类办法，在第1类办法中有3步，在第2类办法中有2步，每步的方法数见箭线下面的mi，i=1，2，3，4，5。‎ 完成A→B这件事，共有方法数为m1m2m3+m4m5。‎ ‎（2）步中有类情形 从A到D算作完成一件事，简单地记为A→D。完成A→D这件事，需要经历三步，即A→B，B→C，C→D。其中B→C这步又分为三类，这就是步中有类。箭线下面的mi（i=1，2，3，4，5）表示相应步的方法数。‎ 完成A→D这件事，共有方法数为m1(m2+m3+m4)m5。‎ 要点诠释：‎ ‎① 对“类”与“步”的理解，要再上一个层次，可进一步地理解为：“类”用“+”号连结，“步”用“×”号连结，“类”独立，“步”连续，“类”标志一件事的完成，“步”缺一不可。‎ ‎② 使用计数原理解题，大部分离不开分类。分类时，要按一个标准来分，最忌采用双重或多重标准分类。‎ ‎【典型例题】‎ 类型一、分类加法计数原理 ‎ 例1．(2015春 府谷县校级月考)某学校高一年级共8个班，高二年级6个班从中选一个班级担任学校星期一早晨升旗任务，共有（ ）种安排方法。‎ A.8 B.6 C.14 D.48‎ ‎【答案】C ‎【思路点拨】根据题意，分“从高一的班级中选取”和“从高二的班级中选取”2中情况讨论，由分类计算原理计算可得答案。‎ ‎【解析】‎ 根据题意，某学校从高一或高二的班级中选一个班级担任学校升旗任务，‎ 如果从从高一的班级中选取，有8种情况；‎ 如果从从高二的班级中选取，有6种情况。‎ ‎ 则有8+6=14中安排方法；故选：C。‎ ‎【总结升华】‎ ‎ 解决这类问题的关键是搞清分类还是分步．‎ 举一反三：‎ ‎【变式1】书架上有不同的语文书10本，不同的英语书7本，不同的数学书5本，现从中任选一本阅读，不同的选法有（ ）．‎ ‎ A．22种 B．350种 C．32种 D．20种 ‎【答案】应用分类加法计数原理：10+7+5=22（种），故选A。‎ ‎【变式2】从甲地到乙地，一天中，有火车2班，汽车3班，飞机2班，，那么从甲地到乙地共有 种不同的走法。‎ ‎【答案】完成这件事，有三类方法：‎ 第一类是乘火车，有2种不同方法；‎ 第二类是乘汽车，有3种不同方法；‎ 第三类是乘飞机，有2种不同方法。‎ 则完成这件事，依分类加法计数原理，共有N=2+3+2=7种不同方法。‎ ‎【变式3】如图所示，在连接正八边形的三个顶点而成的三角形中，与正八边形 有公共边的三角形有________个．‎ ‎【答案】‎ 类型二、分步乘法计数原理 例2. 设某班有男生30名，女生24名. 现要从中选出男、女生各一名代表班级参加比赛，共有多少种不同的选法？‎ ‎【思路点拨】选出一组参赛代表，可以分两个步骤．第 l 步选男生．第2步选女生．‎ ‎【解析】第 1 步，从 30 名男生中选出1人，有30种不同选择；‎ 第 2 步，从24 名女生中选出1人，有 24 种不同选择．根据分步乘法计数原理，共有30×24 =720‎ 种不同的选法．‎ ‎【总结升华】‎ ‎ 用分步乘法计数原理解决问题时，首先要根据问题的特点，确定一个分步的可行标准；其次还要注意完成这件事情必须且只需连续完成这n个步骤后，这件事情才算圆满完成，这时才能使用分步乘法计数原理．同时，要弄清每一步骤中完成本步骤的方法种数．‎ 举一反三：‎ ‎【变式1】（2018春 甘肃校级期中改编）若将6本不同的书放到5个不同盒子里，有多少种不同方法（ ）‎ A. B. C. D. ‎ ‎【答案】‎ 将6本不同的书放到5个不同的盒子里，每本书都有5种放法，根据乘法原理可得不同放法为种。故选：C。‎ ‎【高清课堂：分类加法计数原理或分步乘法计数原理 389221分步计数原理 练习（2）】‎ ‎【变式2】的展开式中共有多少项？‎ ‎【答案】 。因为展开式的每一项都是从第一括号中取一项，再从第二括号中取一项，再从第三括号中取一项，相乘而得到的，根据分步计数原理共有=项。‎ ‎【变式3】四名运动员争夺三项冠军，不同的结果最多有多少种？‎ ‎【答案】64；‎ 事件实际上是确定三项冠军的得主，“由冠军到运动员”，完成这件事分三步.：‎ 第一步确定第一项冠军的得主，有4种不同结果；‎ 第二步确定第二项冠军的得主，有4种不同结果；‎ 第三步确定第三项冠军得主，有4种不同结果.‎ 则共有4×4×4=64种不同结果。‎ ‎【变式4】如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种？ ‎ ‎【答案】 按地图A、B、C、D四个区域依次分四步完成,‎ ‎ 第一步, m1 = 3 种, 第二步, m2 = 2 种,‎ ‎ 第三步, m3 = 1 种, 第四步, m4 = 1 种,‎ 所以根据乘法原理, 得到不同的涂色方案种数共有N = 3 × 2 ×1×1 = 6 ‎ 类型三、两个原理的对比应用 例3. 某单位职工义务献血，在体检合格的人中，O型血的共有28人， A型血的共有7人，B型血的共有9人，AB型血的共有3人.‎ ‎（1）从中任选1人去献血，有多少种不同的选法？‎ ‎（2）从四种血型的人中各选1人去献血，有多少种不同的选法？‎ ‎【思路点拨】两个问题是该分类还是分步，是解好本题的关键。‎ ‎【解析】‎ ‎（1）任选1人去献血，即无论选哪种血型的哪一个人，这件“任选1人去献血”的事情已做完，故由分类加法计数原理，共有种不同的选法。‎ ‎（2）要从四种血型的人中各选人，即要在每种血型的人中依次选出1人后，这件“各选人去献血”的事情才完成，由分步乘法计数原理，共有种不同的选法。‎ ‎ 【总结升华】‎ ‎ 在用两个原理解决问题时，一定要分清完成这件事，是有，l类办法还是需分成n个步骤．应用分类加法计数原理必须要求各类中的每一种方法都保证完成这件事．应用分步乘法计数原理则是需各步均是完成这件事必须经由的若干彼此独立的步骤．‎ 举一反三：‎ ‎【变式】我校高二级有12名语文教师，13名数学教师，15名英语教师，现从中选出教师参加一个新课程研讨会。‎ ‎（1）若选派1名教师参会，有多少种选派方法？‎ ‎（2）若三个学科各派1名教师参会，有多少种选派方法？‎ ‎（3）若选派2名不同学科的教师参会，有多少种选派方法？‎ ‎【答案】‎ ‎（1）分三类：第一类选语文老师，有12种不同选法；第二类选数学老师，有13种不同选法；第三类选英语老师，有15种不同选法. 共有12+13+15=40种不同的选派方法.‎ ‎(2) 分三步: 第一步选选1名语文老师，有12种不同选法; 第二步选1名数学老师，有13种不同选法；第三步选1名英语老师，有15种不同选法. 共有种不同的选派方法.‎ ‎(3) 分三类: 选1名语文老师和1名数学老师，有种不同选法；选1名语文老师和1名英语老师，有种不同选法；选1名英语老师和1名数学老师，有种不同选法.共有种不同的选派方法.‎ 类型四、两个原理的综合应用 例4．书架上放有3本不同的数学书，5本不同的语文书，6本不同的英语书。若从这些书中取不同的科目的书两本，有多少种不同的取法。‎ ‎【思路点拨】‎ ‎ 从书架上任取不同科目的书两本，可以有3类情况（数语各1本，数英各1本，语英各1本），而在每一类情况中又需分2个步骤才能完成。‎ ‎【解析】‎ ‎(1)第一类：当取1本数学书1本语文书时，分两步完成：‎ 第一步取数学书，有3种不同的报名方法；‎ 第二步取语文书，有5种不同方法；‎ 则共有3×5种不同结果.‎ ‎（2）第二类：当取1本数学书1本英语书时，分两步完成：‎ 第一步取数学书，有3种不同的报名方法；‎ 第二步取英语书，有6种不同方法；‎ 则共有3×6种不同结果.‎ ‎（3）第三类：当取1本语文书1本英语书时，分两步完成：‎ 第一步取语文书，有5种不同的报名方法；‎ 第二步取英语书，有6种不同方法；‎ 则共有5×6种不同结果.‎ 故共得到的不同的取法种数是：3×5+3×6+5×6=63（种）。‎ ‎【总结升华】‎ 当完成事件中既有分类也有分步时，一般先分类，然后再在每一类中分步。‎ 举一反三：‎ ‎【变式1】集合A={1，2，－3}，B={－1，－2，3，4}．现从A、B中各取一个元素作为点P（x，y）的坐标．‎ ‎ （1）可以得到多少个不同的点？‎ ‎ （2）在这些点中，位于第一象限的有几个？‎ ‎【答案】‎ ‎（1）一个点的坐标由x、y两个元素确定，若它们有一个不同，则表示不同的点，可分为两类：‎ ‎ 第一类：选A中的元素为x，B中的元素为y，有3×4=12个不同的点；‎ ‎ 第二类：选A中的元素为y，B中的元素为x，有4×3=12个不同的点；‎ ‎ 由分类计数原理得不同点的个数为12+12=24（个）．‎ ‎ （2）第一象限内的点，即x、y必须为正数，从而只能取A、B中的正数，同样可分为两类，同（1）．‎ ‎ 由分类计数原理得适合题意的不同点的个数为2×2+2×2=8（个）．‎ ‎【变式2】在1～20共20个整数中取两个数相加,使其和为偶数的不同取法共有多少种?‎ ‎【答案】90；‎ 取与取是同一种取法.分类标准为两加数的奇偶性,‎ 第一类,偶偶相加,由分步计数原理得(10×9)/2=45种取法；‎ 第二类,奇奇相加,也有(10×9)/2=45种取法.‎ 根据分类计数原理共有45+45=90种不同取法.‎ ‎【高清课堂：分类加法计数原理或分步乘法计数原理 389221例题4】‎ ‎【变式3】用5种不同颜色给图中A，B，C，D四个区域涂色，每个区域涂一种 颜色. 若要求相邻(有公共边)的区域涂不同颜色，那么共有多少种不同的 D B C A 涂色方法?‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎【答案】 如图所示，将4个小方格依次编号为1,2,3,4，第1个小方格可以从5种颜色中任取一种颜色涂上，有5种不同的涂法．‎ ‎（1）当第2个、第3个小方格涂不同颜色时，有12种不同的涂法，第4个小方格有3种不同的涂法．由分步计数原理可知，有5×12×3＝180种不同的涂法；‎ ‎（2）当第2个、第3个小方格涂相同颜色时，有4种涂法，由于相邻两格不同色，因此，第4个小方格也有4种不同的涂法，由分步计数原理可知．有5×4×4＝80种不同的涂法．‎ 由分类加法计数原理可得，共有180＋80＝260种不同的涂法．‎ 类型五、 枚举法 ‎ 例5. 某电脑用户计划用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘，根据需要，软件至少买3个，磁盘至少买2盒，则不同的选购方式有（ ）．‎ ‎ A．5种 B．6种 C．7种 D．8种 ‎【思路点拨】 本题是一道理财问题，其实质是180元钱如何用，用树状图可解，‎ ‎【解析】可能的选购数表如下：‎ ‎ ‎ ‎ 由题意知，除去购买3个软件，2盒磁盘，剩余的钱数为500－3×60－2×70=180（元）．设用剩余的180元选购单片软件x个，盒装磁盘y盒．‎ ‎ 则 60x+70y≤180（x，y∈N）．‎ ‎ 不等式共有7个解，即选购方式有7种，故选C．‎ ‎ 【总结升华】 本题采用树状图将所有答案一一列出，既清楚又直观．‎ 举一反三：‎ ‎【变式】满足∪=｛1,2｝的集合、共有多少组?‎ ‎【答案】‎ 法一：｛1,2｝的子集：φ,｛1｝,｛2｝,｛1,2｝,但不是随便两个子集搭配都行。可分为四类:‎ ‎1)当=φ时,只有=｛1,2｝,得1组解；‎ ‎2)当=｛1｝时,=｛2｝或=｛1,2｝,得2组解；‎ ‎3)当=｛2｝时,=｛1｝或=｛1,2｝,得2组解；‎ ‎4)当=｛1,2｝时,=φ或｛1｝或｛2｝或｛1,2｝,得4组解.‎ 根据分类计数原理,共有1+2+2+4=9组解.‎ 法二：设、为两个“口袋”,需将两种元素(1与2)装入,任一元素至少装入一个袋中,分两步可办好此事:第1步装“1”,可装入不装入,也可装入不装入,还可以既装入又装入,有3种装法；第2步装2,同样有3种装法.根据分步计数原理共有3×3=9种装法,即原题共有9组解.‎