专题08 立体几何-备战2017高考高三数学（理）全国各地一模金卷分项解析版 40页

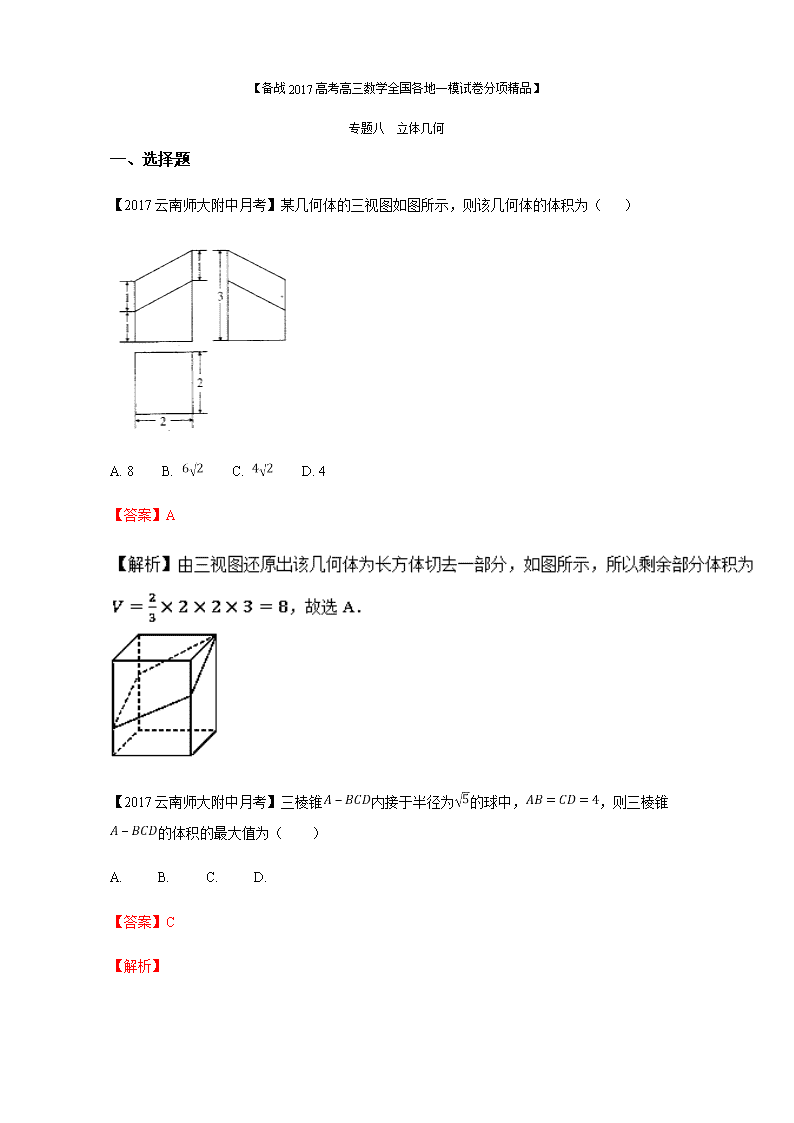
‎【备战2017高考高三数学全国各地一模试卷分项精品】‎ 专题八 立体几何 一、选择题 ‎【2017云南师大附中月考】某几何体的三视图如图所示，则该几何体的体积为（ ）‎ A. 8 B. C. D. 4‎ ‎【答案】A ‎【2017云南师大附中月考】三棱锥内接于半径为的球中，，则三棱锥的体积的最大值为（ ）‎ A. B. C. D. ‎【答案】C ‎【解析】‎ 如图，过作平面，使⊥平面，交于点，设点到的距离为，当球心在上时，最大，此时分别为，的中点，且球心为的中点，所以，所以，故选C．‎ ‎【2017山东菏泽上学期期末】已知是两个不同平面，直线，则“”是“”的（ ）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎【答案】A ‎【解析】‎ 依题意，两平面平行，则一个平面内的直线与另一个平面平行，反之若直线和平面平行，两个平面可能相交，个为充分不必要条件.‎ ‎【2017山东菏泽上学期期末】某几何体的三视图如图所示，在该几何体的各个面中，面积最小的面与底面的面积之比为（ ）‎ A. B. C. D. 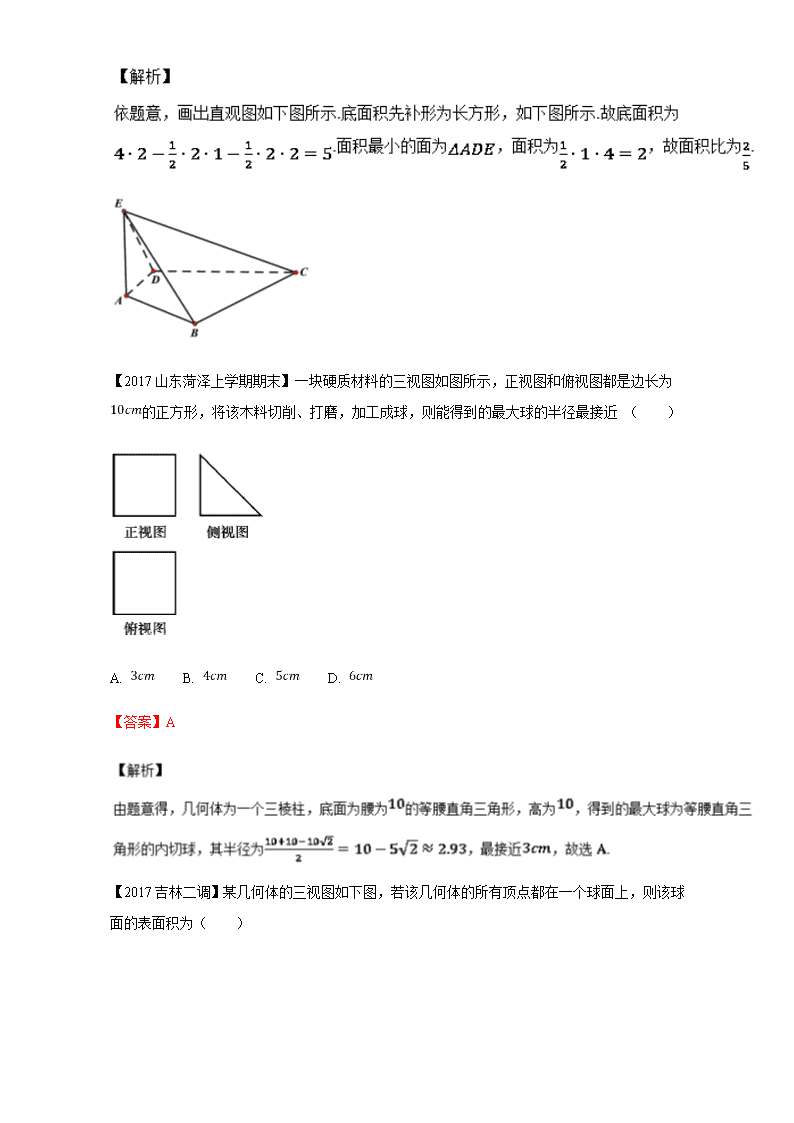‎【答案】C ‎【2017山东菏泽上学期期末】一块硬质材料的三视图如图所示，正视图和俯视图都是边长为的正方形，将该木料切削、打磨，加工成球，则能得到的最大球的半径最接近 （ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【2017吉林二调】某几何体的三视图如下图，若该几何体的所有顶点都在一个球面上，则该球面的表面积为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ 由三视图，可得该几何体是一个正三棱柱（如图所示），其中底面是边长为2的等边三角形，侧棱长为2，由题意可知该几何体的外接球的球心为，半径为，为底面正三角形的中心，则，则该球面的表面积为.故选B.‎ ‎【2017江西师大附中、临川一中联考】某空间几何体的三视图如图所示，则该几何体的体积为( )‎ A. B. C. D. ‎ ‎【答案】B ‎【2017湖北重点中学联考】如图所示，在四边形中，,将沿折起，使得平面平面，构成四面体，则在四面体中，下列说法正确的是（ ）‎ A. 平面平面 B. 平面平面 ‎ C. 平面平面 D. 平面平面 ‎【答案】D ‎【2017湖北重点中学联考】一个几何体的三视图如图所示，则该几何体的外接球的表面积为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ 从题设中三视图所提供的图形信息与数据信息可知该几何体是棱长为的长方体的一角所在三棱锥，其外接球与该长方体的外接球相同，其直径是该长方体的对角线，故球的半径为，所以该外接球的表面面积，应选答案B。‎ ‎【2017河北衡水六调】已知一个底面为正六边形，侧棱长都相等的六棱锥的正视图与俯视图如图所示，若该几何体的底面边长为2，侧棱长为，则该几何体的侧视图可能是 （ ）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【2017江西上饶一模】某几何体的三视图如图所示，则该几何体的体积为（ ）‎ ‎ A．5 B． C． D． ‎ ‎【答案】 ‎ ‎【解析】‎ 几何体如下图，几何体为底面为直角梯形的直四棱柱，截去阴影表示的三棱锥，所以体积为 ,故选D.‎ ‎【2017内蒙包头十校联考】如图，某几何体的正视图、侧视图和俯视图分别是等边三角形、等腰三角形和菱形，则该几何体的体积为（ ）‎ A． 3 B． 4 C. D．‎ ‎【答案】 ‎ ‎【2017内蒙包头十校联考】在正方体中，点在线段上运动，则异面直线与所成角S的取值范围是（ ）‎ A． B． C. D．‎ ‎【答案】 ‎ ‎【解析】‎ 如下图： ,所有异面直线所成的角为,当点在线段上运动时，求的取值范围，点不能与重合，与点重合时，最大，最大为 ，的取值范围是 所以异面直线所成角的取值范围是，故选D.‎ ‎【2017山西五校联考】某几何体的三视图如图所示，则该几何体的表面积为（ ）‎ A． B． ‎ C． D．‎ ‎【答案】 ‎ ‎【2017山西五校联考】已知三棱锥内接与球，且，若三棱锥体积的最大值为，则球的表面积为（ ）‎ A． B． C． D．‎ ‎【答案】 ‎ ‎【点睛】本题考查了球与几何体的问题，是高考中的重点问题，要有一定的空间想象能力，这样才能找准关系，得到结果，一般外接球需要求球心和半径，首先应确定球心的位置，借助于外接球的性质，球心到各顶点距离相等，这样可先确定几何体中部分点组成的多边形的外接圆的圆心，过圆心且垂直于多边形所在平面的直线上任一点到多边形的顶点的距离相等，然后同样的方法找到另一个多边形的各顶点距离相等的直线（这两个多边形需有公共点），这样两条直线的交点，就是其外接球的球心，再根据半径，顶点到底面中心的距离，球心到底面中心的距离，构成勾股定理求解，有时也可利用补体法得到半径，例：三条侧棱两两垂直的三棱锥，可以补成长方体，它们是同一个外接球.‎ ‎【2017广东深圳一模】已知棱长为2的正方体，球与该正方体的各个面相切，则平面截此球所得的截面的面积为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ 因为球与各面相切，所以直径为2，且的中点在所求的切面圆上，所以所求截面为此三点构成的边长为正三角形的外接圆，由正弦定理知，所以面积，选D．‎ ‎【2017荆、荆、襄、宜四地七校联考】某几何体的三视图如图所示，图中的四边形都是边长为的正方形，两条虚线互相垂直，则该几何体的体积是 A. B. C. D.‎ ‎【答案】B ‎【点睛】 1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图．2．三视图中“正侧一样高、正俯一样长、俯侧一样宽”，因此，可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据．‎ 二、填空题 ‎【2017湖北武汉武昌区调研】若四面体的三组对棱分别相等，即，，，给出下列结论：‎ ‎①四面体每组对棱相互垂直；‎ ‎②四面体每个面的面积相等；‎ ‎③从四面体每个顶点出发的三条棱两两夹角之和大于 而小于 ；‎ ‎④连结四面体每组对棱中点的线段相互垂直平分；‎ ‎⑤从四面体每个顶点出发的三条棱的长可作为一个三角形的三边长；‎ 其中正确结论的序号是__________．（写出所有正确结论的序号）‎ ‎【答案】②④⑤‎ ‎【解析】‎ 把四面体补形为平行六面体,由三组对棱分别相等可知此平行六面体为长方体,如图所示,只有长方体为正方体时①才正确,故①不正确.‎ 在长方体中,有△BAC≌△DCA.‎ ‎△ABC≌△DCB,△CBD≌△ADB.‎ ‎∴四面体ABCD每个面的面积都相等,故②正确.‎ 对于③,以∠BAC,∠CAD,∠BAD为例说明.‎ ‎∵△BAC≌△DCA,∴∠CAD=∠ACB.‎ 又∵△DAB≌△CBA,‎ ‎∴∠BAD=∠ABC.‎ ‎∴∠BAC+∠CAD+∠BAD=∠BAC+∠ACB+∠ABC=180°,故③不正确.‎ 对于④,连接四面体ABCD对棱中点的线段即是连接长方体对面中心的线段,显然相互垂直平分,故④正确.‎ 对于⑤,以AB、AC、AD为例进行说明.‎ ‎∵AD=BC,AB、AC、BC三边长可构成△ABC,‎ ‎∴AB、AC、AD可以作为一个三角形的三边长.同理可得从其他顶点出发的三条棱的长也可以作为一个三角形的三边长.故⑤正确.‎ ‎【2017河北衡水六调】已知三棱锥平面，其中，，四点均在球的表面上，则球的表面积为__________．‎ ‎【答案】‎ ‎【点睛】本题考查球的体积与表面积，考查球与长方体之间的关系，考查三棱锥与长方体之间的关系，本题考查几何中常用的一种叫补全图形的方法来完成；本题在解答时，首先根据且平面，得到三棱锥的三条侧棱两两垂直，以三条侧棱为棱长得到一个长方体，由圆的对称性知长方体的各个顶点都在这个球上，长方体的体积就是圆的直径，求出直径，得到圆的面积． ‎ 三、解答题 ‎【2017安徽合肥一模】如图所示，在四棱台中，底面，四边形为菱形，，.‎ ‎（Ⅰ）若为中点，求证：平面；‎ ‎（Ⅱ）求直线与平面所成角的正弦值.‎ ‎【答案】（1）详见解析；（2）.‎ ‎【解析】‎ ‎（Ⅰ）四边形为菱形，，连结，则为等边三角形，‎ 又为中点，，由 得， ,‎ 底面，底面，，又 ,‎ 平面 ‎【点睛】立体几何中计算涉及两个内容一个是面积体积问题，一个是空间的角与距离问题，其中空间角与距离问题可通过空间向量法简化思维量．‎ ‎（1）若两条异面直线和的方向向量分别为，两条异面直线和所成的角为，则；‎ ‎（2）若直线的方向向量为，平面的法向量为，直线与平面所成的角为，则；‎ ‎（3）设分别为二面角的两个半平面的法向量，其二面角大小为，则或，其中．‎ ‎【2017云南师大附中月考】如图，三棱锥中，平面，，，是的中点，是的中点，点在上，.‎ ‎（1）证明：平面；‎ ‎（2）若，求二面角的余弦值.‎ ‎【答案】（Ⅰ）证明过程见解析；（Ⅱ）.‎ ‎（Ⅱ）作BO⊥AC于点O，过点O作OH//PA，‎ 以O为坐标原点，OB，OC，OH所在直线为x轴、y轴、z轴建立如图6所示的空间直角坐标系，‎ 则 ‎∴，‎ 则平面CDA的一个法向量为 设平面CDB的一个法向量为 则 可取，所以，‎ 所以二面角B−CD−A的余弦值为． ‎ ‎【2017湖北武汉武昌区调研】如图，四棱锥中， ，，侧面为等边三角形， , .‎ ‎（Ⅰ）证明：平面;‎ ‎（Ⅱ）求与平面所成角的正弦值.‎ ‎【答案】（Ⅰ）证明过程见解析；（Ⅱ）与平面所成角的正弦值为 ‎【解析】‎ 方法一：空间向量法 ‎（Ⅰ）以为坐标原点，射线为轴正半轴，建立如图所示的空间直角坐标系，则,, ,‎ 设，则 ，‎ 且， ， ，‎ 由,得 ，‎ 解得： ，‎ 由,得 ①‎ 由,得 ②‎ 解①②，得 ，‎ ‎ , , , ,‎ ‎, ,‎ ‎ ,‎ 平面 …………………6分 方法二：综合法 ‎（Ⅰ） 解：如下图，取的中点，连结，，则四边形为矩形，‎ ‎ ‎ ‎ ,‎ 侧面为等边三角形，,‎ ‎,且,‎ 又 ,‎ ‎, ,‎ ‎,‎ 平面.‎ ‎（Ⅱ）过点作于，‎ 因为，，所以平面平面 所以平面平面,‎ 由平面与平面垂直的性质，知平面,‎ 在中，由，得，所以.‎ 过点作平面于，连结，则为与平面所成角的角，‎ 因为 ，平面,‎ 所以平面，所以,‎ 在中，由，求得.‎ 在中， ,所以 ,‎ 由，得 ，‎ 即，解得,‎ 所以,‎ 故与平面所成角的正弦值为.‎ ‎【点晴】本题考查的是线面垂直的判定和直线与平面所成的角，本题中（1）问的关键是结合线面垂直的判定定理证明线和平面内的两条相交直线垂直即可得证；（2）求直线和平面所成角时找到平面的垂线是问题的关键，斜线和斜线在平面的射影所成的角即为直线和平面所成的角，转到直角三角形中求解即可.‎ ‎【2017山东菏泽上学期期末】如图，在三棱柱中，底面，，是棱上一点.‎ ‎（1）求证：；‎ ‎（2）若，求二面角的大小.‎ ‎【答案】（1）证明过程见解析；（2）二面角的大小为.‎ ‎（2）以为原点，分别为轴建立空间直角坐标系.因为，‎ 所以，.‎ 设平面的一个法向量，则，即，令，则，即，又平面的一个法向量，‎ ‎∴，由图可知二面角为锐角，∴二面角的大小为.‎ ‎【2017四川资阳上学期期末】如图，矩形和等边三角形中，，平面平面．‎ ‎（1）在上找一点，使，并说明理由；‎ ‎（2）在（1）的条件下，求平面与平面所成锐二面角余弦值．‎ ‎【答案】（1）证明过程见解析；（2）平面与平面所成锐二面角的余弦值为.‎ ‎（2）由（1）知两两互相垂直，建立空间直角坐标系如图所示，，三角形为等边三角形，．‎ 于是，‎ 设面的法向量，所以，得，‎ 则面的一个法向量，又是线段的中点，‎ 则的坐标为，于是，且，‎ 又设面的法向量，‎ 由，得，取，则，‎ 平面的一个法向量，‎ 所以，‎ 平面与平面所成锐二面角的余弦值为．‎ ‎【2017吉林二调】如图，在四棱锥中，底面是菱形，且，点是棱的中点，平面与棱交于点.‎ ‎（1）求证：；‎ ‎（2）若，平面平面，求平面与平面所成的二面角的余弦值.‎ ‎【答案】（1）详见解析；（2）.‎ ‎【解析】‎ ‎（1）证明：∵是菱形，∴，‎ 又平面，平面，‎ ‎∴平面，‎ ‎∵四点共面，且面面，‎ ‎∴.‎ ‎（2）解：取中点，连接，，‎ ‎∵，∴，‎ ‎∵平面平面，平面平面，‎ ‎∴面，‎ ‎∴，在菱形中，∵，，是中点，‎ ‎∴，‎ 如图，以为原点，、、所在直线为坐标轴建立空间直角坐标系，‎ 由得，，，，，‎ ‎，.‎ 又∵，点是棱中点，∴点是棱中点，‎ ‎∴，，，‎ 设平面的法向量为，‎ 则有，，取，则.‎ ‎∵平面，∴是平面的一个法向量，‎ ‎，二面角的余弦值为，‎ ‎∴平面与平面所成的二面角的余弦值为.‎ ‎【2017江西师大附中、临川一中联考】如图1，在中，是边的中点，现把沿折成如图2所示的三棱锥，使得．‎ ‎（1）求证：平面平面；‎ ‎（2）求平面与平面夹角的余弦值．‎ ‎【答案】(1详见解析，(2) ‎ ‎（2）因为平面，且，故可如图建立空间直角坐标系，则 ‎，， ‎ 设平面的法向量为，则由得；‎ 同理可求得平面的法向量为， ‎ 故所求角的余弦值.‎ ‎【2017湖北重点中学联考】如图，在直三棱柱中，平面侧面，且 ‎（1）求证：;‎ ‎（2）若直线与平面所成的角为，请问在线段上是否存在点，使得二面角的大小为，请说明理由.‎ ‎【答案】(1)详见解析， (2) ‎ ‎（2）由（1），则直线与平面所成的角 所以，又，所以 ‎ 假设在线段上是否存在一点，使得二面角的大小为 由是直三棱柱，所以以点为原点，以所在直线分别为轴建立空间直角坐标系，如图所示，且设，则由，，得 ‎ 所以，‎ 设平面的一个法向量，由， 得：‎ ‎，取 ‎ 由（1）知，所以平面的一个法向量 所以，解得 ‎∴点为线段中点时，二面角的大小为 ‎ ‎【2017河北衡水六调】四棱锥中，底面为直角梯形，，，，且平面平面．‎ ‎（1）求证：；‎ ‎（2）在线段上是否存在一点，使二面角的大小为，若存在，求出的值；若不存在，请说明理由．‎ ‎【答案】（1）见解析；（2）．‎ ‎【解析】‎ ‎ (1)过点作，交于，连接．‎ ‎∵，‎ ‎∴四边形是矩形，‎ ‎∴，‎ ‎∵，‎ ‎∴，‎ ‎∴，∴，‎ 又平面平面，‎ ‎∴平面，∵平面，‎ ‎∴；‎ ‎【点睛】利用空间向量法求二面角的一般方法，设二面角的平面角为，设分别为平面的法向量，二面角的大小为，向量的夹角为，则有（图1）或 （图2）其中.‎ ‎ ‎ 图1 图2‎ ‎【2017江西上饶一模】在三棱柱中，已知侧面是菱形，侧面是正方形，点在底面的投影为的中点．‎ ‎（1）证明：平面平面；‎ ‎（2）设为上一点，且，求二面角的正弦值．‎ ‎【答案】(1)详见解析；（2）.‎ ‎（2）如图所示，以点为坐标原点建立空间直角坐标系，‎ 不妨设菱形边长为2，易知，，，因为为中点且有，所以，‎ 又因为平面为菱形，所以为等边三角形，‎ 从而，从而，‎ 所以点的坐标为，‎ 因为，所以，‎ 又因为，所以，‎ 设平面的法向量为，‎ ‎，，‎ 所以即 令，则，，所以，‎ 易知平面的法向量，‎ 所以，‎ 所以，‎ 从而二面角的正弦值为．‎ ‎【2017内蒙包头十校联考】如图，四边形为正方形，平面,‎ ‎（1）证明：平面平面；‎ ‎（2）求二面角的正弦值.‎ ‎【答案】（1）详见解析；（2）.‎ ‎（2）依题意，,设是平面的一个法向量，则，即，‎ 因此可取……7分 设是平面的一个法向量，则，即，‎ 因此可取……9分 所以，……11分 故二面角的正弦值为……12分 ‎【2017山西五校联考】如图，在四棱锥中，平面．‎ ‎（1）在线段上确定一点，使得平面平面，并说明理由；‎ ‎（2）若二面角的大小为，求二面角的余弦值．‎ ‎【答案】(1) 点为的中点时，平面平面;(2). ‎ ‎【解析】‎ ‎（1）如图，当点为的中点时，平面平面， 1分 理由如下：‎ 因为为的中点，‎ 所以，所以四边形为平行四边形，所以，‎ 因为，所以，‎ 因为平面，平面，所以，又因为，‎ 所以平面，因为平面，所以平面平面，‎ 所点点为的中点时，平面平面． 5分 ‎（2）分别以所在的直线为轴，轴建立如图所示的空间直角坐标系，‎ 其中轴，易得平面，所以，‎ 所以是二面角的平面角，大小为，所以， 7分 设，则，‎ 所以，‎ 所以， 8分 设平面的法向量为，则，即，‎ 令，则，所以， 10分 因为平面，所以是平面的一个法向量，‎ 设二面角的大小为，由图可知为锐角，‎ 则． 12分 ‎【2017广东深圳一模】如图，四边形为菱形，四边形为平行四边形，设与相交于点，．‎ ‎（1）证明：平面平面；‎ ‎（2）若与平面所成角为60°，求二面角的余弦值．‎ ‎【答案】（1）见解析；（2）．‎ ‎【解析】‎ ‎（1）证明：连接，‎ ‎∵四边形为菱形，‎ ‎∵，‎ 在和中，‎ ‎，，‎ ‎∴，‎ ‎∴，‎ ‎∴，‎ ‎∵，‎ ‎∴平面，‎ ‎∵平面，‎ ‎∴平面平面；‎ ‎（2）‎ 解法二：如图，在平面内，过作的垂线，交于点，由（1）可知，平面平面，‎ ‎∴平面，‎ ‎∴直线两两互相垂直，‎ 分别为轴建立空间直角坐标系，‎ 易得为与平面所成的角，∴，‎ 则，‎ ‎，‎ 设平面的一个法向量为，则 且，‎ ‎∴，且 取，可得平面的一个法向量为，‎ 同理可求得平面的一个法向量为，‎ ‎∴，‎ ‎∴二面角的余弦值为．‎ ‎【2017荆、荆、襄、宜四地七校联考】如图，在四棱锥中，底面是平行四边形，，侧面底面，，， 分别为的中点，点在线段上．‎ ‎ ‎ ‎（Ⅰ）求证：平面； （Ⅱ）如果直线与平面所成的角和直线与平面所成的角相等，求的值．‎ ‎【答案】（Ⅰ）详见解析（Ⅱ） ‎【解析】‎ ‎（Ⅰ）证明：在平行四边形中，因为，，‎ ‎ 所以．由分别为的中点，得， ‎ ‎ 所以． …………2分 ‎ 因为侧面底面，且，所以底面． ‎ 又因为底面，所以． …………4分 ‎ ‎ 又因为，平面，平面， ‎ ‎ 所以平面． ………………6分 ‎ ‎【点睛】利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出平面的法向量；第四，破“应用公式关”.‎