【数学】2019届一轮复习 人教A版 几何证明选讲 作业 7页

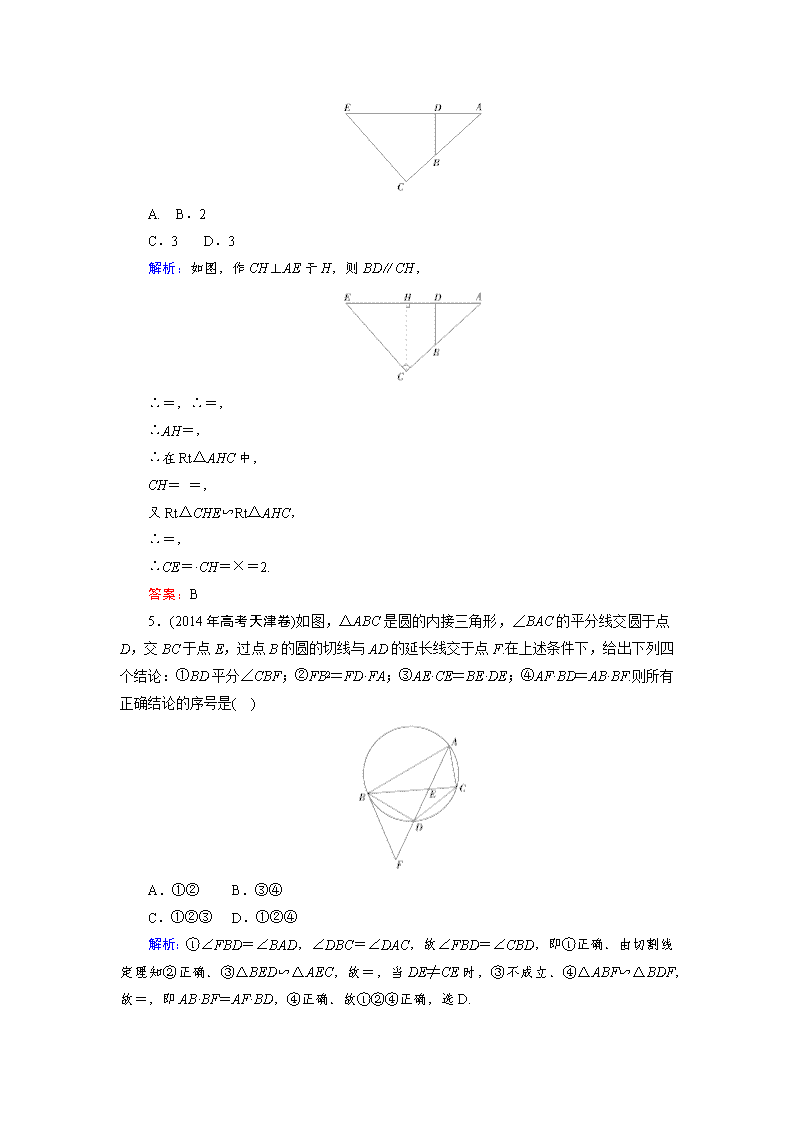
几何证明选讲 A 组 考点基础演练 一、选择题 1．在△ABC 中，点 D 在线段 BC 上，∠BAC＝∠ADC，AC＝8，BC＝16，则 CD 为( ) A．3 B．4 C．5 D．6 解析：∵∠BAC＝∠ADC，∠C 为公共角，∴△ABC∽△DAC，∴＝，∴CD＝＝＝4. 故选 B. 答案：B 2．如图，在▱ABCD 中，E 是 BC 上一点，BE∶EC＝2∶3，AE 交 BD 于 F，则 BF∶FD 等于( ) A．2∶5 B．3∶5 C．2∶3 D．5∶7 解析：∵AD＝BC，BE∶EC＝2∶3， ∴BE∶AD＝2∶5. ∵AD∥BC， ∴BF∶FD＝BE∶AD＝2∶5. 答案：A 3.如图，在四边形 ABCD 中，EF∥BC，FG∥AD，则＋＝( ) A．1 B．2 C．3 D．4 解析：∵EF∥BC，∴＝， 又∵FG∥AD，∴＝， ∴＋＝＋＝＝1. 答案：A 4.如图，BD⊥AE，∠C＝90°，AB＝4，BC＝2，AD＝3，则 CE＝( ) A. B．2 C．3 D．3 解析：如图，作 CH⊥AE 于 H，则 BD∥CH， ∴＝，∴＝， ∴AH＝， ∴在 Rt△AHC 中， CH＝ ＝， 又 Rt△CHE∽Rt△AHC， ∴＝， ∴CE＝·CH＝×＝2. 答案：B 5．(2014 年高考天津卷)如图，△ABC 是圆的内接三角形，∠BAC 的平分线交圆于点 D， 交 BC 于点 E，过点 B 的圆的切线与 AD 的延长线交于点 F.在上述条件下，给出下列四个结 论：①BD 平分∠CBF；②FB2＝FD·FA；③AE·CE＝BE·DE；④AF·BD＝AB·BF.则所有正确 结论的序号是( ) A．①② B．③④ C．①②③ D．①②④ 解析：①∠FBD＝∠BAD，∠DBC＝∠DAC，故∠FBD＝∠CBD，即①正确．由切割线 定理知②正确．③△BED∽△AEC，故＝，当 DE≠CE 时，③不成立．④△ABF∽△BDF， 故＝，即 AB·BF＝AF·BD，④正确．故①②④正确，选 D. 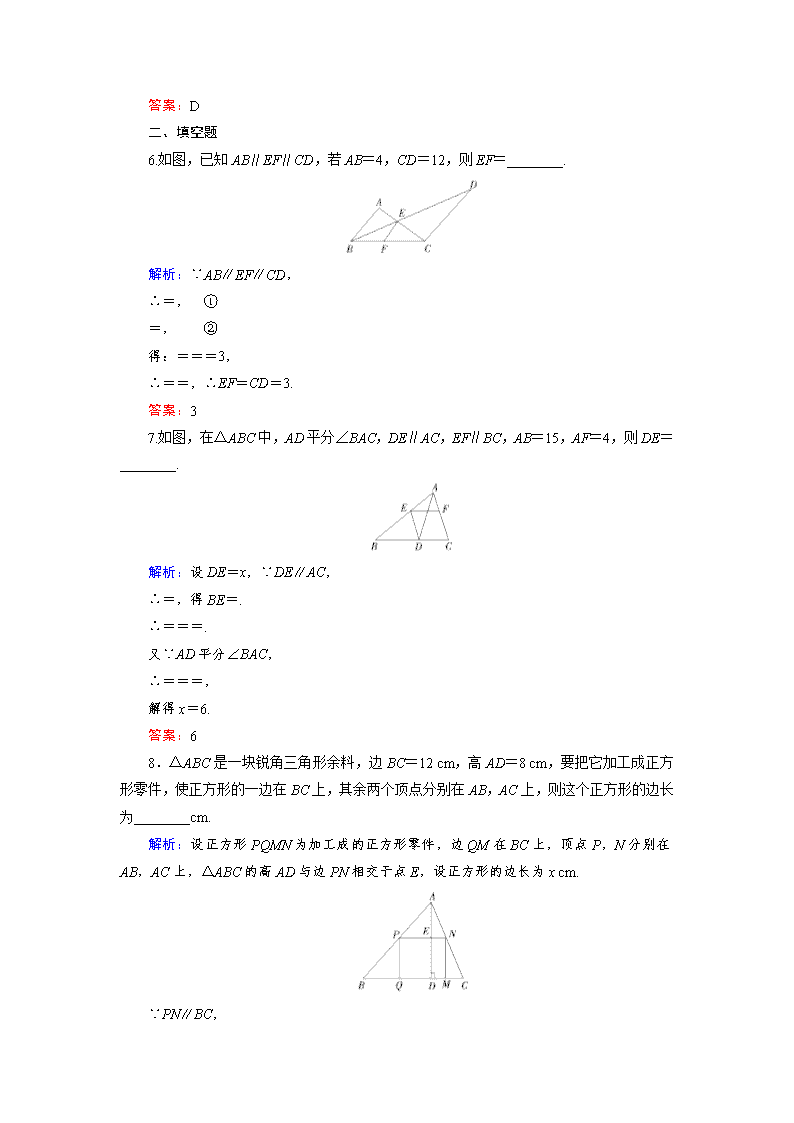答案：D 二、填空题 6.如图，已知 AB∥EF∥CD，若 AB＝4，CD＝12，则 EF＝________. 解析：∵AB∥EF∥CD， ∴＝， ① ＝， ② 得：＝＝＝3， ∴＝＝，∴EF＝CD＝3. 答案：3 7.如图，在△ABC 中，AD 平分∠BAC，DE∥AC，EF∥BC，AB＝15，AF＝4，则 DE ＝________. 解析：设 DE＝x，∵DE∥AC， ∴＝，得 BE＝. ∴＝＝＝. 又∵AD 平分∠BAC， ∴＝＝＝， 解得 x＝6. 答案：6 8．△ABC 是一块锐角三角形余料，边 BC＝12 cm，高 AD＝8 cm，要把它加工成正方 形零件，使正方形的一边在 BC 上，其余两个顶点分别在 AB，AC 上，则这个正方形的边长 为________cm. 解析：设正方形 PQMN 为加工成的正方形零件，边 QM 在 BC 上，顶点 P，N 分别在 AB，AC 上，△ABC 的高 AD 与边 PN 相交于点 E，设正方形的边长为 x cm. ∵PN∥BC， ∴△APN∽△ABC. ∴＝，∴＝. 解得 x＝4.8. 即加工成的正方形零件的边长为 4.8 cm. 答案：4.8 三、解答题 9.如图，△ABC 中，D 是 AC 的中点，E 是 BC 延长线上一点，过 A 作 AH∥BE.连接 ED 并延长交 AB 于 F，交 AH 于 H.如果 AB＝4AF，EH＝8，求 DF 的长． 解析：∵AH∥BE，∴＝. ∵AB＝4AF，∴＝. ∵HE＝8，∴HF＝2. ∵AH∥BE，∴＝. ∵D 是 AC 的中点，∴＝1. ∵HE＝HD＋DE＝8，∴HD＝4， ∴DF＝HD－HF＝4－2＝2. 10.(2015 年绵阳一模)如图，△ABC 中，AB＝AC，∠BAC＝90°，AE＝AC，BD＝AB， 点 F 在 BC 上，且 CF＝BC.求证： (1)EF⊥BC； (2)∠ADE＝∠EBC. 证明：设 AB＝AC＝3a， 则 AE＝BD＝a，CF＝ a. (1)＝＝，＝＝. 又∠C 为公共角，故△BAC∽△EFC， 由∠BAC＝90°.∴∠EFC＝90°，∴EF⊥BC. (2)由(1)得 EF＝ a， 故＝＝，＝＝， ∴＝.∵∠DAE＝∠BFE＝90°， ∴△ADE∽△FBE，∴∠ADE＝∠EBC. B 组 高考题型专练 1.(2014 年西安模拟)如图，在△ABC 中，M，N 分别是 AB，BC 的中点，AN，CM 交于 点 O，那么△MON 与△AOC 面积的比是________． 解析：∵M，N 分别是 AB，BC 中点，故 MN 綊 AC， ∴△MON∽△COA，∴＝2＝. 答案：1∶4 2．(2014 年佛山质检)如图，在直角梯形 ABCD 中，DC∥AB，CB⊥AB，AB＝AD＝a， CD＝，点 E，F 分别为线段 AB，AD 的中点，则 EF＝________. 解析：连接 DE 和 BD，依题知，EB∥DC，EB＝DC＝，CB⊥AB，∴EBCD 为矩形，∴ DE⊥AB，又 E 是 AB 的中点，所以△ABD 为等腰三角形．故 AD＝DB＝a，∵E，F 分别是 AD，AB 的中点，∴EF＝DB＝a. 答案： 3．已知圆的直径 AB＝13，C 为圆上一点，过 C 作 CD⊥AB 于 D(AD>BD)，若 CD＝6， 则 AD＝________. 解析：如图，连接 AC，CB，∵AB 是⊙O 的直径，∴∠ACB＝90°. 设 AD＝x，∵CD⊥AB 于 D， ∴由射影定理得 CD2＝AD·DB， 即 62＝x(13－x)， ∴x2－13x＋36＝0， 解得 x1＝4，x2＝9. ∵AD>BD，∴AD＝9. 答案：9 4．如图，在矩形 ABCD 中，AB＝，BC＝3，BE⊥AC，垂足为 E，则 ED＝________. 解析：在 Rt△ABC 中，BC＝3，AB＝，所以∠BAC＝60°.因为 BE⊥AC，AB＝，所以 AE＝，在△EAD 中，∠EAD＝30°，AD＝3，由余弦定理知，ED2＝AE2＋AD2－2AE·AD·cos ∠EAD＝＋9－2××3×＝，故 ED＝. 答案： 5.如图所示，在△ABC 中，AB＝AC，过点 A 的直线与其外接圆交于点 P，交 BC 的延 长线于点 D. (1)求证：＝； (2)若 AC＝3，求 AP·AD 的值． 解析：(1)因为∠CPD＝∠ABC，∠PDC＝∠PDC， 所以△DPC∽△DBA，所以＝. 又 AB＝AC，所以＝. (2)因为∠ABC＋∠APC＝180°，∠ACB＋∠ACD＝180°，∠ABC＝∠ACB，所以∠ACD ＝∠APC. 又∠CAP＝∠DAC，所以△APC∽△ACD，所以＝. 所以 AP·AD＝AC2＝9. 6.如图，在△ABC 中，D 是 AC 的中点，E 是 BD 的三等分点，AE 的延长线交 BC 于 F， 求的值． 解析：过 D 点作 DM∥AF 交 BC 于 M，因为 DM∥AF， 所以＝＝， 因为 EF∥DM， 所以＝， 即 S△BDM＝9S△BEF， 又＝， 即 S△DMC＝S△BDM＝6S△BEF， 所以 S 四边形 DEFC＝14S△BEF， 因此＝.