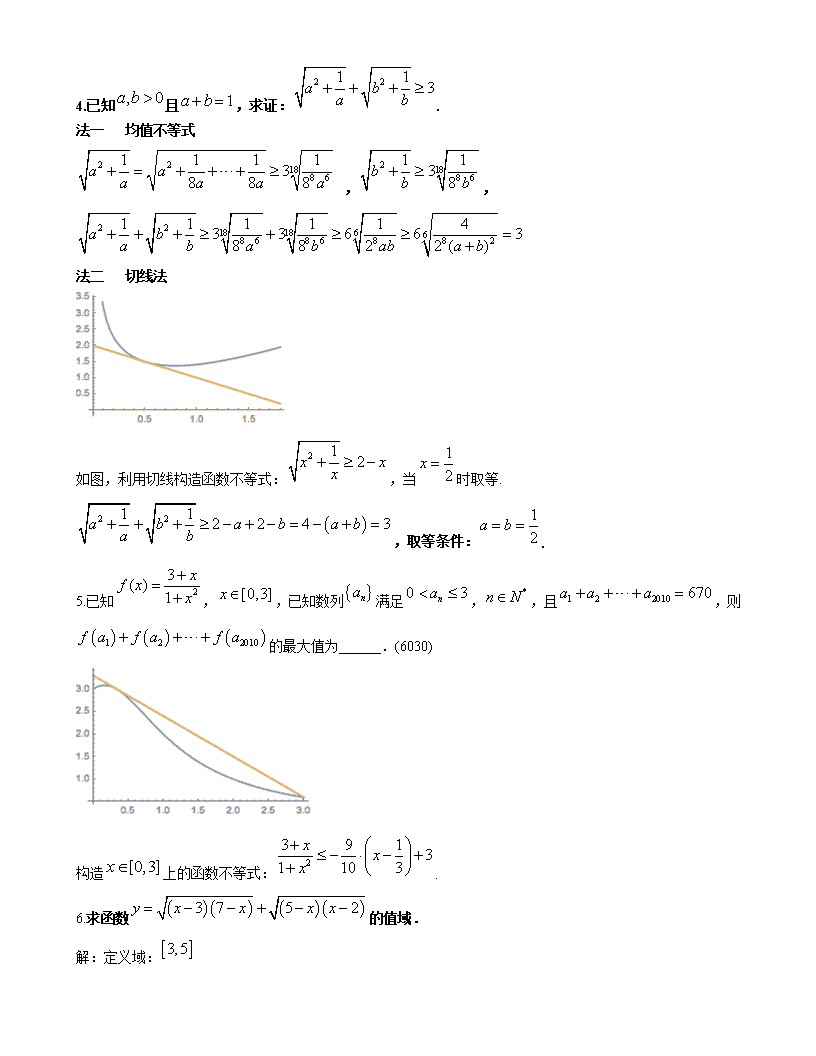【数学】2021届一轮复习人教A版导数专题之切割线放缩学案 14页

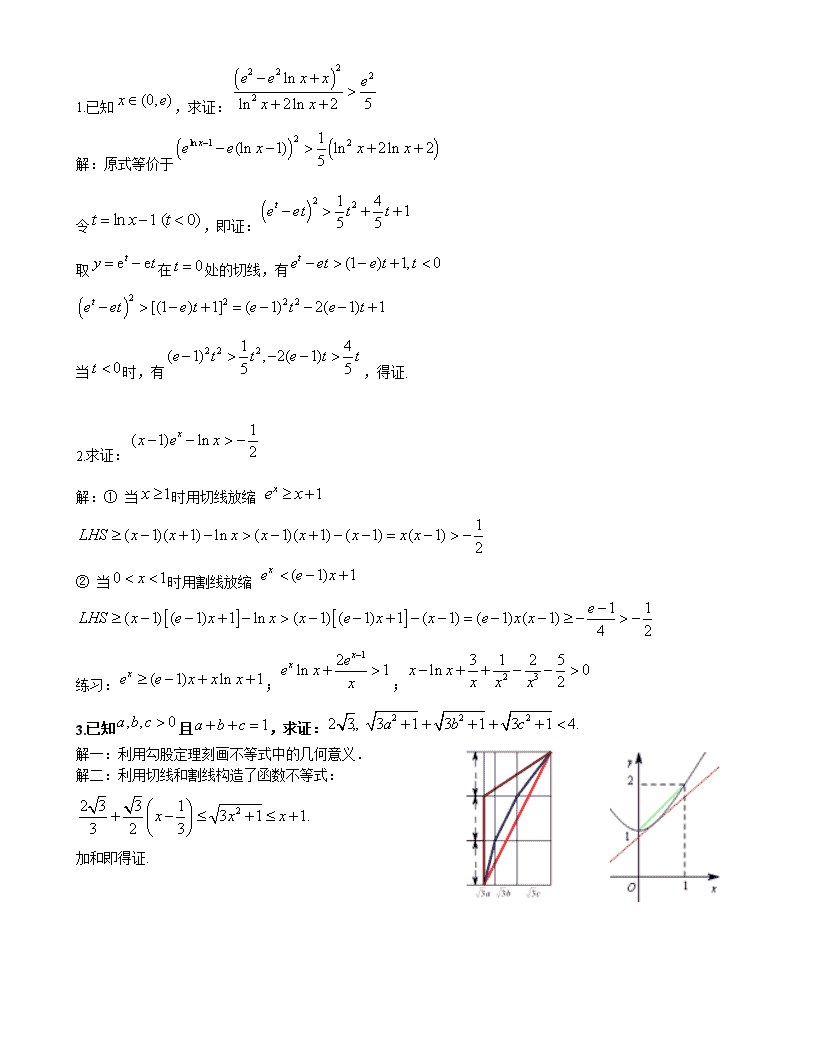
导数专题之切割线放缩 切线放缩 若函数在区间上有凹凸性，可以利用切线进行放缩．‎ ‎（1）若函数的图象在区间下凸（），则有：；‎ ‎（2）若函数的图象在区间上凸（），则有：.‎ 割线放缩 若函数在区间上有凹凸性，可以利用割线进行放缩．‎ ‎（1）若函数的图象在区间下凸（），则有：；‎ ‎（2）若函数的图象在区间上凸（），则有：.‎ 附 函数凹凸性的定义 ‎1、凹函数定义：设函数在区间上连续，对，若恒有，则 称的图象是上凹/下凸的，函数为上凹/下凸函数；二阶导数 ‎2、凸函数定义：设函数在区间上连续，对，若恒有，则 称的图象是下凹/上凸的，函数为下凹/上凸函数. 二阶导数 ‎1.已知，求证：‎ 解：原式等价于 令，即证：‎ 取在处的切线，有 当时，有，得证.‎ ‎2.求证：‎ 解：① 当时用切线放缩 ‎ ‎② 当时用割线放缩 ‎ 练习：；；‎ ‎3.已知且，求证：‎ 解一：利用勾股定理刻画不等式中的几何意义．‎ 解二：利用切线和割线构造了函数不等式：‎ ‎ ‎ 加和即得证.‎ ‎4.已知且，求证：.‎ 法一    均值不等式 ‎ ，，‎ 法二    切线法 如图，利用切线构造函数不等式：，当时取等.‎ ‎，取等条件：.‎ ‎5.已知，，已知数列满足，，且，则的最大值为______．(6030)‎ 构造上的函数不等式：.‎ ‎6.求函数的值域．‎ 解：定义域：‎ ‎， 为上凸函数，于是 ‎，‎ 当且仅当时取等.‎ 当且仅当，即时取等.‎ 于是函数值域为.‎ ‎7.已知且，求的最小值.‎ 解：设函数，‎ ‎，‎ 取这两个函数平行的切线，有 ，即 与联立，解得 ‎8.已知，，则的最大值是______，最小值是_______．‎ 法一　割线放缩处理最大值.‎ ‎， ‎ 等号当时取得．于是有 考虑到，于是当时右边取得最大值．因此所求的最大值为．‎ 切线放缩处理最小值．‎ ‎， ‎ 等号当时取得．令 ‎ ‎ 等号当时取得．因此所求的最小值为．‎ 法二 令 ‎ ‎9.已知满足，求的最值.‎ 解：设函数，，‎ 作出函数的图象，函数的图象在处的切线：，以及函数的图象过点和的割线：，如图．‎ 于是可得： ‎ 左侧等号当或时取得；右侧等号当时取得．因此原式的最大值为，当 时取得；最小值为，当，时取得．‎ ‎10.已知，，求证：.‎ 解：设函数， ‎ 取其在和处的切线，分别为和，如图．‎ 直线与直线，函数的图象和直线分别交于 ，则有： ‎ ‎ ‎ 注1　类似的，我们还可以用割线和来估计的下界，如图．‎ 注2　我们也可以利用函数图象的外接曲线得到更加精确的界，例如用和，如图．‎ ‎11.设为非负实数，满足，则的取值范围是______．‎ 设函数，考虑利用切割线放缩得到辅助不等式：‎ 当时，有：‎ 且左边不等式等号当时取得；右边不等式等号当时取得．‎ 左边不等式为：，右边不等式为：，容易得证.‎ 所以 ‎ 左侧等号当时可以取得；右侧等号当时可以取得．因此所求的取值范围是．‎ ‎12.已知，求证：．‎ 解：先证 ‎ 于是当时，有 ‎ 当时，利用在和之间的割线，有 ‎ 利用在处的展开，有 ‎ 于是当时，有 ‎ 右侧对应的 ，得证.‎ ‎13.已知，，则的最小值是_______．‎ 根据切割线放缩，有 ，于是 进而 ‎ 等号当且仅当时取得．因此所求的最小值为4．‎ ‎14.已知，求的最小值．‎ 解　切线放缩 ‎ ‎ ‎ 当时取到等号，从而得到所求的最小值为2n．‎ 注 切比雪夫不等式亦可解.‎ 例1、，已知数列满足，且满足，则= 6030 ‎ 解析：，当时，=6030‎ 对于函数,,在处的切线方程为即，‎ 则成立，‎ 所以当时，有 例2、已知函数．‎ ‎（1）求在上的最大值；‎ ‎（2）若直线为曲线的切线，求实数的值；‎ ‎（3）当时，设，且，若不等式恒成立，求实数的最小值．‎ 解析：（1）， ‎ 令，解得（负值舍去），由，解得．‎ ‎（ⅰ）当时，由，得，在上的最大值为．‎ ‎（ⅱ）当时，由，得，在上的最大值为．‎ ‎（ⅲ）当时，在时，，在时，，‎ 在上的最大值为． ‎ ‎（2）设切点为，则 由，有，化简得， 即或， …① 由，有，…②‎ 由①、②解得或． ‎ ‎（3）当时，，由（2）的结论直线为曲线的切线，‎ ‎，点在直线上，根据图像分析，曲线在线下方． ‎ 下面给出证明：当时，． ‎ ‎，‎ 当时，，即．‎ ‎ ，‎ ‎， ‎ ‎．‎ 要使不等式恒成立，必须． ‎ 又当时，满足条件，‎ 且，因此，的最小值为． ‎ 例3、若，且，则++≤‎ 证明：设，则 ，，‎ 由得，得或，‎ 故在是上凸的，在区间，是下凸的.‎ 由，则平衡值，由导数知识易求得在处的切线为 ，‎ 因，在是上凸的，故恒成立.‎ 即，，，三式相加并结合即得++≤.‎ 若将该题条件改为：若，且时，解法同理.‎ 此时平衡值，而在处的切线为, 因，在是下凸的，故恒成立.‎ 即，，，三式相加并结合即得++≥.‎ 即得一个新的不等式：若，且，则++≥.‎ 所以，在证明一类多元不等式时，我们经常用到的一个办法就是假设这些变元的和为1.‎ 例4、若实数，证明：.‎ 提示：不妨设，则平衡点是.在处的切线，有.‎ ‎5、若非负，且，证明：‎ 提示：平衡点是.在的切线，有 练习1：已知函数，‎ ‎⑴求函数在定义域上的单调区间.‎ ‎⑵若关于的方程恰有两个不等的实根，求实数的范围；‎ ‎⑶已知实数，，若不等式在上恒成立，求实数的最小值.（可以利用切线求的最大值）‎ 练习2：若非负，且，证明：‎ 提示：平衡点是.在的切线，有 切线放缩法实质就是利用函数的图像性质解决一类多元的问题向一元函数求最值和类型的不等式转化.此时，可以选择先求二阶导看凹凸性，判断这个函数是否能使用切线法，或者能够被用得比较好.也可以直接选择求一阶导，把等号取道条件的切线值求出来，对应不等式常数项配最后的常数系数.其本质相当于求这个一元函数在等号取到条件时（也就是文中的平衡点）的切线值，进一步求对于这个一元函数相对应的某个局部不等式.‎ ‎15.已知函数 ‎（1）求函数的单调区间；‎ ‎（2）若对任意实数都成立，求k的取值范围.‎ 解：（1） ‎ 设，‎ 于是在上单调递减，在上单调递增，在处取得极小值，亦为最小值，因此在R单调递增．‎ ‎（2） ‎ 设 ， ‎ 其极值点在附近．因此考虑在处进行切线放缩，有 ‎ ‎ ‎ 设 ，‎ 在取最小值，，即.‎ 数学小王子王海刚，沈阳飞跃教育首席数学专家，才华横溢，年少有为，被付斌等大神称为“中国导数第一人”、 “放缩大师”。王老师年仅30，已出版两本数学专著：数学小丸子的解题笔记(导数压轴题与放缩应用)、数学小丸子的导数题典（仅就这点而言，已经秒杀众多特高级专家教师）。这两本书都堪称导数经典，尤其是前者，囊括了市面上几乎所有的导数解题技巧，简直是导数中的“圣经”，秒杀数学的创始人唐鑫老师评价这本书独具一格、系统完备、后人难以超越，用前无古人后无来者来形容也不为过。‎ ‎ ‎ 近几年，王老师作为专家多次应邀到各省市顶尖中学指导导数的教学，得到众多优秀教师和学生的顶礼膜拜。‎ 目前，数学小王子王海刚正在闭关研究秒杀高中解析几何的技巧，不出半年，就将出版解析几何的解题笔记，相信届时这本书又将成为解析几何领域开天辟地的圣经级作品。‎ 王老师对数学的爱疯狂到了无以复加的地步，每天至少十五六个小时做数学，仅睡不到6个小时，因此非常高产。他的数学博客访问量已接近两百万人次，可见其水准之高，远超兰琪、张平、郑小彬、王永喜等大神，而且还在持续更新中。这让我想到了莫扎特，大家都只看到莫扎特天才的表演，却不知道他自幼每天十多个小时的辛苦训练。其实王老师的本科专业是社会学，属于文科，他能有今日的数学才华也是归功于近七八年的刻苦钻研。‎ 在小小王子（公主）即将诞生之际，王老师正奋笔疾书，期待早日完成著作，献给可爱的宝宝以及众多的学生、数学教师和数学爱好者。王老师的两本著作预计春节前后面世，让我们一起期待吧！‎ QQ：446903172 电话：15542157349‎