2018届二轮复习第24讲三角函数解析式的求法学案（全国通用） 9页

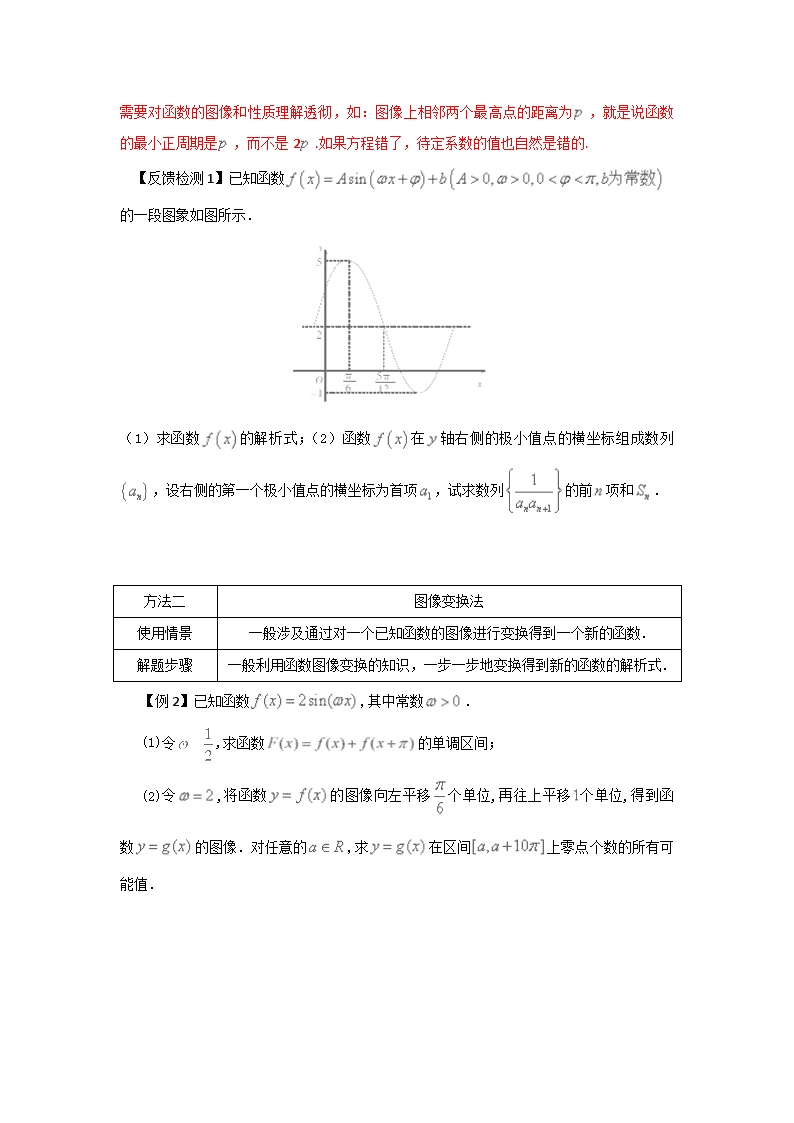
‎【知识要点】‎ 三角函数的解析式的求法一般有三种：待定系数法、图像变换法和代入法.‎ ‎【方法讲评】‎ 方法一 待定系数法 使用情景 一般知道函数的图像或图像的特征.‎ 解题步骤 一般先设出三角函数的解析式，再求待定系数，最值确定函数的,周期确定函数的,非平衡位置的点确定函数的.‎ ‎【例1】 已知函数的图像关于直线对称，且图像上相邻两个最高点的距离为.‎ ‎（1）求函数的解析式；（2）若，求的值.‎ ‎（2）由（1）得所以，又得所以， ‎ ‎.‎ ‎【点评】利用待定系数法求三角函数的解析式，需要建立关于各个待定系数的方程，这需要对函数的图像和性质理解透彻，如：图像上相邻两个最高点的距离为，就是说函数的最小正周期是，而不是2.如果方程错了，待定系数的值也自然是错的.‎ ‎【反馈检测1】已知函数的一段图象如图所示．‎ ‎（1）求函数的解析式；（2）函数在轴右侧的极小值点的横坐标组成数列，设右侧的第一个极小值点的横坐标为首项，试求数列的前项和．‎ 方法二 图像变换法 使用情景 一般涉及通过对一个已知函数的图像进行变换得到一个新的函数.‎ 解题步骤 一般利用函数图像变换的知识，一步一步地变换得到新的函数的解析式.‎ ‎【例2】已知函数,其中常数．‎ ‎(1)令,求函数的单调区间；‎ ‎(2)令,将函数的图像向左平移个单位,再往上平移个单位,得到函数的图像．对任意的,求在区间上零点个数的所有可能值．‎ ‎【点评】利用图像变换法求函数的解析式时，要对函数图像变换（平移变换、伸缩变换、对称变换和翻折变换）比较熟练，不要出错. 学 ‎ ‎【反馈检测2】已知函数的周期为,且 ,将函数图像上的所有点的横坐标伸长为原 的倍（纵坐标不变）,再将所得图像向右平移个单位长度后得到函数的图像.‎ ‎（1）求函数与的解析式；‎ ‎（2）是否存在,使得按照某种顺序成等差数列？若存在,请求出的值，若不存在,说明理由；‎ ‎（3）求实数与正整数,使得在内恰有2013个零点．‎ 方法三 代入法 使用情景 一般知道函数的一部分图像或图像的特征，求另外对称的一半的解析式.‎ 解题步骤 一般先在所求的函数的图像上任意取一点，再求出点的对称点，再把点的坐标代入已知的函数的解析式化简即得所求函数的解析式.‎ ‎【例3】 定义在区间上的函数的图象关于直线对称,当时函数图象如图所示．‎ ‎(1)求函数在的表达式；(2)求方程的解；‎ ‎(3)是否存在常数的值,使得在上恒成立;若存在,求出的取值范围;若不存在,请说明理由．‎ ‎(2)当时, ∴ ‎ ‎ 即,当时, ∴∴方程的解集是 ‎ ‎【点评】(1)这种方法关键在于理解，这种处理方法有点类似求轨迹方程里的“代入法”.可以把已知的图像上的点看作“主动点”，对称图像上的点看作是“被动点”，这样就好理解些了.(2)求对称点的坐标时，一般利用对称的知识列方程求解，不要算错了.‎ ‎【反馈检测3】设函数(－)－．‎ ‎(1)求的最小正周期及单调递增区间；‎ ‎(2)若函数与的图象关于点对称，求当时，函数的值域．‎ 高中数学常见题型解法归纳及反馈检测第24讲：‎ 三角函数解析式的求法参考答案 ‎【反馈检测1答案】（1）；（2）.‎ ‎【反馈检测2答案】（1），；（2）不存在；（3），.学 ‎ ‎【反馈检测2详细解析】（1）由函数的周期为可得，，又由，得，所以；将函数的图像上所有点的横坐标伸长到原 的2倍（保持纵坐标不变）后可得的图像，再将的图象向右平移个单位长度后得到函数 ‎.‎ ‎（3）令，即，当时，显然不成立；当时，‎ ‎，令，则当时，.由函数及，的图像可知，当时，在内有3个解.再由可知，，综上所述，，.‎ ‎【反馈检测3答案】（1）,单调递增区间为[－，＋]，；（2）值域为.‎ ‎【反馈检测3详细解析】(1)由题意知＝sin－cos－1＝sin(－)－1，所以的最小正周期＝＝6．由－≤－≤＋，，得－≤≤＋，，所以的单调递增区间为[－，＋]，．‎ ‎(2)因为函数与的图象关于直线对称，设点是函数图像上一点，则其关于点（0,1）对称的点必在函数的图像上，所以= 所以-‎ 所以函数的值域为.‎