甘肃省白银市靖远县2019届高三第三次联考数学（文）试题 19页

高三数学考试（文科）‎ 一、选择题：本题共12小题每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.下列格式的运算结果为实数的是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 利用复数运算化简每个选项即可求解 ‎【详解】对A,‎ 对B,‎ 对C, ‎ 对D,‎ 故选D ‎【点睛】本题考查复数的运算，熟记运算法则是关键，是基础题 ‎2.设集合，，则集合可以为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 先求得集合A,再依次验证选项即可.‎ ‎【详解】因为，可以依次验证选项，得到当时，.‎ 故答案为D.‎ ‎【点睛】这个题目考查了集合的交集运算，属于基础题目.‎ ‎3.在平行四边形中，,,则点的坐标为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ 分析】‎ 先求,再求,即可求D坐标 ‎【详解】，∴，则D(6,1)‎ 故选A ‎【点睛】本题考查向量的坐标运算，熟记运算法则，准确计算是关键，是基础题 ‎4.若函数，则（ ）‎ A. 2 B. ‎4 ‎C. -2 D. -4‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ ‎，可得，结合，从而求得结果.‎ ‎【详解】∵，∴，‎ ‎∵，∴，‎ 故选A.‎ ‎【点睛】该题考查的是有关函数值的求解问题，在解题的过程中，涉及到的知识点有奇函数的性质，属于简单题目，注意整体思维的运用.‎ ‎5.从某小学随机抽取100名学生，将他们的身高（单位：厘米）分布情况汇总如表：‎ 身高 ‎（100，110]‎ ‎（110，120]‎ ‎（120，130]‎ ‎（130，140]‎ ‎（140，150]‎ 频数 ‎5‎ ‎35‎ ‎30‎ ‎20‎ ‎10‎ 由此表估计这100名小学生身高的中位数为（　　）（结果保留4位有效数字）‎ A. B. C. D. 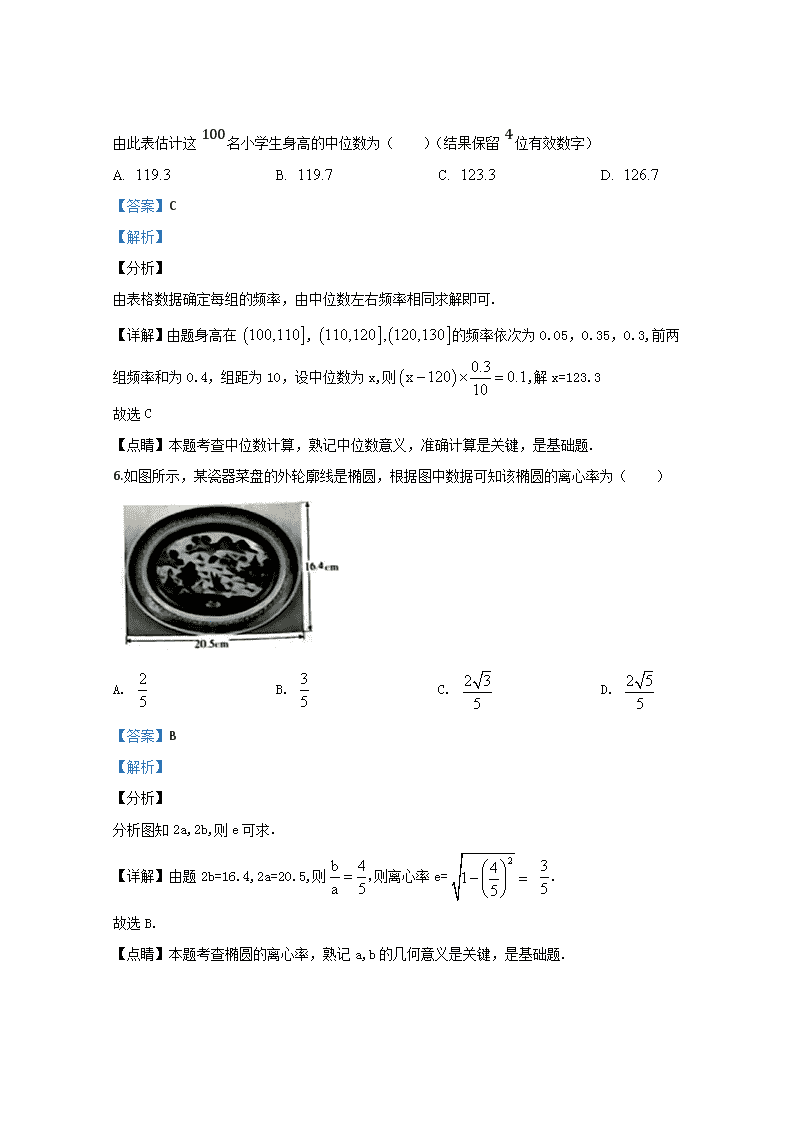‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 由表格数据确定每组的频率，由中位数左右频率相同求解即可.‎ ‎【详解】由题身高在,的频率依次为0.05，0.35，0.3,前两组频率和为0.4，组距为10，设中位数为x,则,解x=123.3‎ 故选C ‎【点睛】本题考查中位数计算，熟记中位数意义，准确计算是关键，是基础题.‎ ‎6.如图所示，某瓷器菜盘的外轮廓线是椭圆，根据图中数据可知该椭圆的离心率为（　　）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 分析图知‎2a,2b,则e可求.‎ ‎【详解】由题2b=16.4,‎2a=20.5,则则离心率e= .‎ 故选B.‎ ‎【点睛】本题考查椭圆的离心率，熟记a,b的几何意义是关键，是基础题.‎ ‎7.设满足约束条件则的最大值为（ ）‎ A. 7 B. ‎5 ‎C. 0 D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 作出约束条件对应的可行域，利用线性规划的知识，通过平移即可求得的最大值.‎ ‎【详解】如图，作出约束条件表示的可行域，‎ 由图可知，当直线经过点时，取得最大值7，‎ 故选A.‎ ‎【点睛】该题考查的是有关线性规划的问题，注意目标函数的形式，属于简单题目.‎ ‎8.在中，为边上一点，若，，，，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 先在三角形中用余弦定理计算出的值，然后在三角形中用余弦定理求得的长.‎ ‎【详解】在三角形中，由余弦定理得.在三角形中，由余弦定理得.故选B.‎ ‎【点睛】本小题主要考查利用余弦定理计算角的余弦值和边长，属于基础题.‎ ‎9.汉朝时，张衡得出圆周率的平方除以16等于，如图，网格纸上的小正方形的边长为1，粗实线画出的是某几何体的三视图，俯视图中的曲线为圆，利用张衡的结论可得该几何体的体积为（　　）‎ A. 32 B. ‎40 ‎C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 将三视图还原，即可求组合体体积 ‎【详解】将三视图还原成如图几何体：半个圆柱和半个圆锥的组合体，底面半径为2，高为4，则体积为，利用张衡的结论可得 故选C ‎【点睛】本题考查三视图，正确还原，熟记圆柱圆锥的体积是关键，是基础题 ‎10.若直线与曲线相切，则（ ）‎ A. 3 B. C. 2 D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 设切点为，对求导，得到，从而得到切线的斜率，结合直线方程的点斜式化简得切线方程，联立方程组，求得结果.‎ ‎【详解】设切点为，‎ ‎∵，∴‎ 由①得，‎ 代入②得，‎ 则，，‎ 故选A.‎ ‎【点睛】该题考查的是有关直线与曲线相切求参数的问题，涉及到的知识点有导数的几何意义，直线方程的点斜式，属于简单题目.‎ ‎11.已知函数，则下列判断错误的是（ ）‎ A. 为偶函数 B. 的图像关于直线对称 C. 值域为 D. 的图像关于点对称 ‎【答案】D ‎【解析】‎ ‎【分析】‎ 化简f（x）＝1+2cos4x后，根据函数的性质可得．‎ ‎【详解】f（x）＝1+cos（4x）sin（4x）＝1+2sin（4x）＝1+2cos4x，‎ f（x）为偶函数，A正确；‎ ‎4x得当k=1时，B正确；‎ 因为2cos4x的值域为 ，C正确；‎ 故D错误．‎ 故选D．‎ ‎【点睛】本题考查三角恒等变换，三角函数的性质，熟记三角函数基本公式和基本性质，准确计算是关键，是基础题 ‎12.在棱长为的正方体中，为棱上一点，且到直线与的距离相等，四面体的每个顶点都在球的表面上，则球的表面积为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 由题，先确定F的位置，由互相垂直，构造以为棱的长方体，求其外接球半径即可求得球的表面积 ‎【详解】过做面B,∴面NF,∴FN为到直线的距离，则,设解得x=,‎ 互相垂直, 以为棱的长方体球心即为O，则 球的表面积为4‎ 故选D ‎【点睛】本题考查椎体的外接球，明确点F的位置是突破点，构造长方体是关键，是中档题 二、填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡中的横线上.‎ ‎13.函数的值域为__________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 将函数按照自变量的范围分两种情形分析，根据一次函数的单调性可以求得函数在上的值域为，结合指数函数的单调性可以求得在上的值域为，两者取并集求得结果.‎ ‎【详解】因为在上的值域为，‎ 在上的值域为，‎ 故的值域为，‎ 故答案是：.‎ ‎【点睛】该题考查的是有关分段函数的值域的求解问题，注意分段来处理即可，属于简单题目.‎ ‎14.小张要从种水果中任选种赠送给好友，其中芒果、榴莲、椰子是热带水果，苹果、葡萄是温带水果，则小张送的水果既有热带水果又有温带水果的概率为________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 确定基本事件个数即可求解 ‎【详解】由题从种水果中任选种的事件总数为 ‎ 小张送的水果既有热带水果又有温带水果的基本事件总数为小张送的水果既有热带水果又有温带水果的概率为 故答案为 ‎15.若，，则__________．‎ ‎【答案】-1‎ ‎【解析】‎ ‎【分析】‎ 根据,利用两角差的正切公式计算即可得结果.‎ ‎【详解】 .‎ ‎【点睛】该题考查的是有关角的正切值的求解，涉及到的知识点有两角差的正切公式，属于简单题目.‎ ‎16.已知，分别是双曲线：的左、右顶点，为上一点，则的外接圆的标准方程为__________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由点为上，求m,由外心设外心坐标M(0,t),M在PB的中垂线上求t即可 ‎【详解】为上一点,,解得m=1,则B(1,0),∴PB中垂线方程为+2,令x=0,则y=3,设外接圆心M(0,t),则M(0,3),,∴ 外接圆的标准方程为 故答案为 ‎【点睛】本题考查圆的标准方程，双曲型方程，熟记外心的基本性质，准确计算是关键，是基础题 三、解答题：本大题共6小题，共70分.‎ 解答应写出文字说明、证明过程或演算步骤第17~21题为必考题，每道试题考生都必须作答第22、23题为选考题，考生根据要求作答.‎ ‎（一）必考题：共60分.‎ ‎17.设为等差数列的前项和，已知，.‎ ‎（1）求；‎ ‎（2）设，求数列的前19项和.‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）首先根据题意，列出关于和方程组，求解之后利用等差数列的求和公式求得结果；‎ ‎（2）求得的通项公式，之后应用裂项相消法求和得结果.‎ ‎【详解】（1）∵，‎ ‎∴，‎ ‎∴.‎ ‎（2）设，‎ 则，‎ 故 .‎ ‎【点睛】该题考查的是有关数列的问题，涉及到的知识点有数列的通项公式和求和公式，以及裂项相消法求和，属于中档题目.‎ ‎18.如图，在三棱柱中，平面，为边上一点，，.‎ ‎（1）证明：平面平面.‎ ‎（2）若，试问：是否与平面平行？若平行，求三棱锥的体积；若不平行，请说明理由.‎ ‎【答案】（1）详见解析；（2）两者平行，且.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用平面，证得平面，得到，利用余弦定理证得，由此证得平面，从而证得平面平面.（2）取的中点，连接，通过证明四边形为平行四边形，证得,同理证得,所以平面平面，由此证得平面.利用求得三棱锥的体积.‎ ‎【详解】(1)证明：因为AA1⊥平面ABC，‎ 所以BB1⊥平面ABC，‎ 因为，‎ 所以AD⊥BB1．‎ 在△ABD中，由余弦定理可得，，‎ 则，‎ 所以AD⊥BC，‎ 又，‎ 所以AD⊥平面BB‎1C1C，‎ 因为，‎ 所以平面ADB1⊥平面BB‎1C1C．‎ ‎(2)解：A‎1C与平面ADB1平行．‎ 证明如下：取B‎1C1的中点E，连接DE，CE，A1E，‎ 因为BD＝CD，所以DE∥AA1，且DE＝AA1，‎ 所以四边形ADEA1为平行四边形，‎ 则A1E∥AD．‎ 同理可证CE∥B1D．‎ 因为，‎ 所以平面ADB1∥平面A1CE，‎ 又，‎ 所以A‎1C∥平面ADB1．‎ 因为AA1∥BB1，‎ 所以，‎ 又，且易证BD⊥平面AA1D，‎ 所以．‎ ‎【点睛】本小题主要考查面面垂直的证明，考查线面垂直的证明以及三棱锥体积的求法，属于中档题.‎ ‎19.某小学举办“父母养育我，我报父母恩”的活动，对六个年级（一年级到六年级的年级代码分别为1，2…，6）的学生给父母洗脚的百分比y%进行了调查统计，绘制得到下面的散点图．‎ ‎（1）由散点图看出，可用线性回归模型拟合y与x的关系，请用相关系数加以说明；‎ ‎（2）建立y关于x的回归方程，并据此预计该校学生升入中学的第一年（年级代码为7）给父母洗脚的百分比．‎ 附注：参考数据： ‎ 参考公式：相关系数，若r＞0.95，则y与x的线性相关程度相当高，可用线性回归模型拟合y与x的关系．回归方程中斜率与截距的最小二乘估计公式分别为＝ ，．‎ ‎【答案】（1）详见解析；（2）见解析.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）计算得，代入计算公式求值即可判断与的线性相关程度；（2）由公式计算求带入回归直线求得进而求得回归方程，将x=7代入直线，即可确定百分比 ‎【详解】（1）因为 所以，‎ 所以，‎ 因为所以，‎ 所以 由于与的相关系数约为，说明与的线性相关程度相当高，从而可用线性回归模型拟合与的关系.‎ ‎(2)‎ 因为，所以 所以回归方程为 将，代入回归方程可得，‎ 所以预计该校学生升入中学的第一年给父母洗脚的百分比为.‎ ‎【点睛】本题考查相关系数r,回归直线方程，熟练运用公式计算是关键，是基础题 ‎20.已知是抛物线上一点，为的焦点．‎ ‎（1）若，是上的两点，证明：，，依次成等比数列．‎ ‎（2）若直线与交于，两点，且，求线段的垂直平分线在轴上的截距．‎ ‎【答案】（1）见解析；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由在抛物线上，求出抛物线方程；根据抛物线焦半径公式可得，，的长度，从而证得依次成等比数列；（2）将直线代入抛物线方程，消去，根据韦达定理求解出，从而可得中点坐标和垂直平分线斜率，从而求得 垂直平分线所在直线方程，代入求得结果.‎ ‎【详解】（1）是抛物线上一点 ‎ ‎ 根据题意可得：，，‎ ‎，，依次成等比数列 ‎（2）由，消可得 ‎，‎ ‎ ‎ 设的中点 ‎，‎ 线段的垂直平分线的斜率为 故其直线方程为 当时，‎ ‎【点睛】本题考查抛物线的几何性质、直线与抛物线综合问题，关键在于能够通过直线与抛物线方程联立，得到韦达定理的形式，从而准确求解出斜率.‎ ‎21.已知函数.‎ 讨论的单调性.‎ 若，求的取值范围.‎ ‎【答案】（1）在上单调递增，在上单调递减，在上单调递增；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎ 讨论当，时导数符号变化情况求得单调性由的讨论知：时，,解；时，<0,解符合；当时，，构造函数，，求导判单调性解a的不等式；时，,解a范围，则问题得解 ‎【详解】（1） ‎ 当时，，；，.‎ 所以上单调递增，在上单调递减，在上单调递增.‎ 当时，对恒成立，所以在上单调递增.‎ 当时，，；，.‎ 所以在上单调递增，在上单调递减，在上单调递增.‎ ‎（2）①当时，由（1）知在上单调递增，则在上单调递增，‎ 所以 ，解得 ‎②当时，由（1）知在上单调递减，在上单调递增.‎ 当时，在上单调递增.‎ 所以 对恒成立，则符合题意；‎ 当时，在上单调递减，在上单调递增.‎ 所以.‎ 设函数，，‎ 易得知时 ，‎ 所以，‎ 故对恒成立，即符合题意.‎ 当时，在上单调递减.‎ 所以 对恒成立，则符合题意.‎ 综上所述：的取值范围为.‎ ‎【点睛】本题考查函数与导数的综合问题，导数与函数单调性与最值，不等式有解问题，分类讨论思想，明确分类标准，不重不漏是关键，是中档题 ‎（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.‎ ‎22.在直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，圆的极坐标方程为．‎ ‎（1）若与相交于两点，，求；‎ ‎（2）圆的圆心在极轴上，且圆经过极点，若被圆截得的弦长为，求圆的半径．‎ ‎【答案】（1）6；（2）13.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）将直线参数方程代入圆的直角坐标方程，利用求解得到结果；（2）写出的普通方程并假设圆的直角坐标方程，利用弦长为建立与的关系，再结合圆心到直线距离公式得到方程，解方程求得，即为圆的半径.‎ ‎【详解】（1）由，得 将代入，得 设两点对应的参数分别为，则 故 ‎（2）直线的普通方程为 设圆的方程为 圆心到直线的距离为 因为，所以 解得：或（舍）‎ 则圆的半径为 ‎【点睛】本题考查直线参数方程中参数的几何意义、极坐标与直角坐标的互化、参数方程化普通方程.解决直线参数方程问题中距离之和或积的关键，是明确直线参数方程标准形式中的参数的几何意义，将距离问题转化为韦达定理的形式.‎ ‎23.设函数.‎ ‎（1）求不等式的解集；‎ ‎（2）证明：.‎ ‎【答案】（1）；（2）详见解析.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）零点分段法去绝对值解不等式即可；（2）零点分段分情况证明再由绝对值不等式证明即可 ‎【详解】（1）∵，∴，即，‎ 当时，显然不合；‎ 当时，，解得；‎ 当时，，解得.‎ 综上，不等式的解集为.‎ ‎（2）证明：当时，；‎ 当时，，‎ 则；‎ 当时，，‎ 则.‎ ‎∵，∴.‎ ‎∵，∴.‎ 故.‎ ‎【点睛】本题考查绝对值不等式的解法，证明不等式，熟练运算是关键，是中档题