数学文卷·2018届云南省临沧市第一中学高三下学期第一次月考（2018 11页

临沧市一中 2017—2018 学年下学期高三第 1 次月考 (文科)数学试卷 一、 选择题：本大题共 12 小题，每小题 5 分，共 60 分.在每个小题给出的四个选项中， 有且只有一项符合题目要求. 1.已知全集U Z ， {0 1 2 3}A  ，，， ， 2{x|x 2x}B   ，则  UA C B 为 A.  1,3 B.  0,2 C.  0,1,3 D.  2 2．若复数 2 i 1 2iz   ,则 z = A. 4 B. 1 C. 0 D. -2 3.为了让大家更好地了解我市的天气变化情况，我市气 象局公布了近年来我市每月的日平均最高气温与日平均 最低气温，现绘成雷达图如图所示，下列叙述不正确的是 A．各月的平均最高气温都不高于 25 度 B．七月的平均温差比一月的平均温差小 C．平均最高气温低于 20 度的月份有 5 个 D．六月、七月、八月、九月的平均温差都不高于 10 度 4.已知函数 3log ( ), 0,( ) ( 2), 0, x xf x f x x      则 (2017)f  A．1 B． 0 C． 1 D． 3log 2 5. 设双曲线 2 2 2 2 1(a 0,b 0)x y a b - = > > 的右焦点是 F，左、右顶点分别是 1 2A ,A ,过 F 做 1 2A A 的垂线与双曲线交于 B，C 两点，若 1 2A B A C , 则双曲线的渐近线的斜率为 A ． 1 2 ± B． 2 2 ± C． 1± D ． 2± 6．已知{an}是公差为 1 的等差数列，Sn 为{an}的前 n 项和．若 S8＝4S4，则 a10＝ A ． 17 2 B. 19 2 C. 10 D. 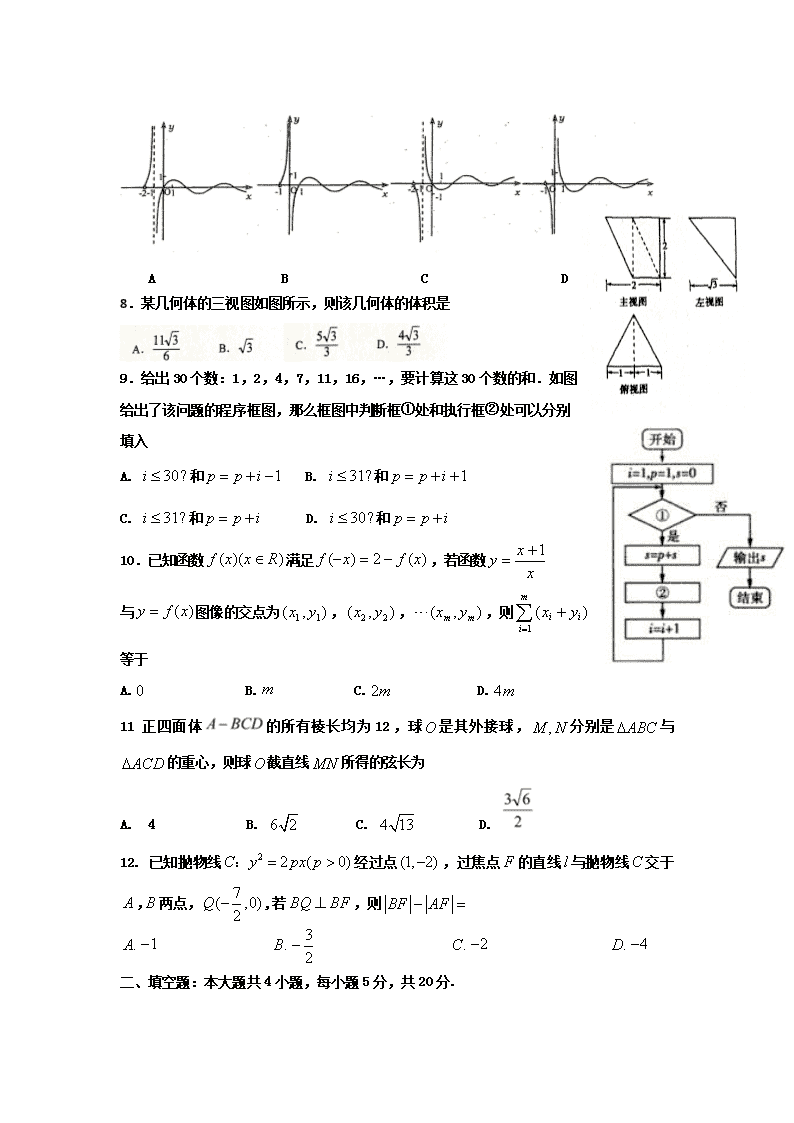12 7. 函数     sin ln 2 xf x x   的图象可能是 A B C D 8．某几何体的三视图如图所示，则该几何体的体积是 9．给出 30 个数：1，2，4，7，11，16，…，要计算这 30 个数的和．如图 给出了该问题的程序框图，那么框图中判断框①处和执行框②处可以分别 填入 A. 30?i  和 1p p i   B. 31?i  和 1p p i   C. 31?i  和 p p i  D. 30?i  和 p p i  10．已知函数 ))(( Rxxf  满足 )(2)( xfxf  ，若函数 x xy 1 与 )(xfy  图像的交点为 ),( 11 yx ， ),( 22 yx ， ),( mm yx ，则    m i ii yx 1 )( 等于 A. 0 B. m C. m2 D. m4 11 正四面体 的所有棱长均为 12，球 O 是其外接球， ,M N 分别是 ABC 与 ACD 的重心，则球 O 截直线 MN 所得的弦长为 A. 4 B. 6 2 C. 4 13 D. 12. 已知抛物线 2 2 ( 0)C y px p ： 经过点 (1, 2) ，过焦点 F 的直线 l 与抛物线 C 交于 A ， B 两点， 7( ,0)2Q  ,若 BQ BF ，则 BF AF  .A 1 .B 3 2  .C 2 .D 4 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分. 13. 已知实数 ,x y 满足条件 1 1 0 4 0 y x y x y          , 则 2z x y  的最大值是 14. 某公司招聘员工，有甲、乙、丙三人应聘并进行面试，结果只有一人被录用，当 三人 被问到谁被录用时， 甲说：丙没有被录用；乙说：我被录用；丙说：甲说的是真话. 事实证明，三人中只有一人说的是假话，那么被录用的人是 15．已知平面向量 a 与 b 的夹角为 3  ，  1 3a , ， 2 2 3 a b ，则 b  . 16. 正整数数列 na 满足 1 1 ,{ 2 3 1, n n n n n a aa a a    是偶 是奇 ，已知 7 2a  ，  na 的前 7 项和的最 大值为 S ，把 1a 的所有可能取值按从小到大排成一个新数列 nb ，  nb 所有项和为T ， 则 S T  . 三、解答题 （本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演算步骤.） 17. （本小题满分 12 分）在 中， 是边 上的点， ， . (Ⅰ)求 ； (Ⅱ)若 ，求 的面积. 18．（本小题满分 12 分）如图，在底面为梯形的四棱锥 S ABCD 中，已知 / /AD BC ， 60ASC   ， 2AD DC  ， 2SA SC SD   ． (Ⅰ)求证： AC SD ； (Ⅱ)求三棱锥 B SAD 的体积． 19．（本小题满分 12 分）一只药用昆虫的产卵数 y 与一定范围内的温度 x 有关, 现收集了 该种药用昆虫的 6 组观测数据如下表： 温度 x/ C 21 23 24 27 29 32 产卵数 y/个 6 11 20 27 57 77 经 计 算 得 ： 6 1 1 266 i i x x    ， 6 1 1 336 i i y y    ，   6 1 ( ) 557i i i x x y y     ，   6 2 1 84i i x x    ， 6 2 1 ( ) 3930i i y y    ，线性回归模型的残差平方和 6 2 1 ( ) 236.ˆ 64i i i y y    ，e8.0605≈3167，其 中 xi, yi 分别为观测数据中的温度和产卵数，i=1, 2, 3, 4, 5, 6. (Ⅰ)若用线性回归模型，求 y 关于 x 的回归方程 ˆy = ˆb x+ ˆa （精确到 0.1）； (Ⅱ)若用非线性回归模型求得 y 关于 x 的回归方程为 ˆy =0.06e0.2303x，且相关指数 R2=0.9522. ( i )试与(Ⅰ)中的回归模型相比，用 R2 说明哪种模型的拟合效果更好. ( ii )用拟合效果好的模型预测温度为 35 C 时该种药用昆虫的产卵数（结果取整数）. 附：一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线 ˆy = ˆb x+ ˆa 的斜率和截距的最小二 乘估计为     1 2 1 ( ) ,ˆ n i ii n ii x x y y b x x         ˆa = y − ˆbx ；相关指数 R2= 2 1 2 1 ( ) 1 ( ) ˆn i ii n ii y y y y        ． 20．（本小题满分 12 分）已知椭圆x2 a2＋y2 b2＝1(a＞b＞0)经过点(0， 3)，离心率为1 2 ，左、右 焦点分别为 F1(－c，0)，F2(c，0)． (Ⅰ)求椭圆的方程； (Ⅱ)若直线 l：y＝－1 2 x＋m 与椭圆交于 A，B 两点，与以 F1F2 为直径的圆交于 C，D 两点， 且满足|AB| |CD| ＝5 3 4 ，求直线 l 的方程． 21. （本小题满分 12 分）已知函数 ln( ) 1 xf x x   ． (Ⅰ)确定函数 ( )f x 在定义域上的单调性； (Ⅱ)若 ( ) xf x ke 在 (1, ) 上恒成立，求实数 k 的取值范围． （二）选考题：共 10 分.请考生在第 22、23 题中任选一题作答，如果多做，则按所做的第 一题计分. 22. [选修 4−4：坐标系与参数方程]（10 分） 已知直线l 的参数方程为 )0(sin2 cos         为参数，tty tx ，以坐标原点 O 为极点， x 轴正半轴为极轴建立极坐标系，曲线 C 的极坐标方程为 1 ， l 与 C 交于不同的两点 21,PP (Ⅰ)求 的取值范围； (Ⅱ)以 为参数，求线段 21PP 中点 M 的轨迹的参数方程. 23. [选修 4−5：不等式选讲]（10 分） 已知函数 |2||4|)(  xxxf (Ⅰ)求不等式 2)( xf 的解集； (Ⅱ)设 )(xf 的最小值为 M , 若 Max 2 的解集包含 ]10[ ，，求 a 的取值范围. 临沧市一中 2017—2018 学年下学期高三第 1 次月考 数学（文科）参考答案 一、选择题：ABCBC BABDB CB 二、填空题：13. 7; 14. 甲; 15.2 16.64 三、解答题 （本大题共 6 小题，共 70 分.解答应写出文字说明、证明过程或演算步骤.） 17．解：（1）在 中， ， 得 由 ，得 在 中，由正弦定理得 ，所以 （2）因为 ， 是锐角，所以 设 ，在 中， 即 化简得： 解得 或 （舍去）则 由 和 互补，得 所以 的面积 18． （Ⅰ）设O 为 AC 的中点，连接 ,OS OD ， ,SA SC OS AC   , ,DA DC DO AC   又 ,OS OD  平面 SOD ，且OS DO O ， AC 平面 SOD ，又 SD  平面 SOD AC SD  （Ⅱ）连接 BD ，在 ASC 中， ,SA SC 060ASC  ，O 为 AC 的中点， ASC 为正三角形，且 2, 3AC OS  ， 在 ASC 中， 2 2 24DA DC AC   ，O 为 AC 的中点， 090ADC  ，且 1OD  ， 在 SOD 中， 2 2 2OS OD SD  SOD 为直角三角形，且 090SOD  SO OD  又OS AC ，且 AC DO O SO  平面 ABCD 1 3 1 1 1 1 32 2 33 2 3 2 3 B SAD S BAD BADV V S SO AD CD SO                   19．(Ⅰ)由题意得，     6 1 6 2 1 ( ) 557 6.6ˆ ,84 i ii ii x x y y b x x           ∴ ˆa 33−6.6 26=−138.6， ∴y 关于 x 的线性回归方程为 ˆy =6.6x−138.6． (Ⅱ) ( i )由所给数据求得的线性回归方程为 ˆy =6.6x−138.6，相关指数为 R2= 6 2 1 6 2 1 ( ) 236.641 1 1 0.0602 0.9398.3930( ) ˆi ii ii y y y y             因为 0.9398＜0.9522， 所以回归方程 ˆy =0.06e0.2303x 比线性回归方程 ˆy =6.6x−138.6 拟合效果更好． ( ii )由( i )得当温度 x=35 C 时， ˆy =0.06e0.2303 35=0.06 e8.0605． 又∵e8.0605≈3167， ∴ ˆy ≈0.06 3167≈190（个）． 即当温度 x=35 C 时，该种药用昆虫的产卵数估计为 190 个． 20．(1)由题设知 b＝ 3， c a ＝1 2 ， b2＝a2－c2， 解得 a＝2， b＝ 3， c＝1， ∴椭圆的方程为x2 4 ＋y2 3 ＝1. (2)由题设，以 F1F2 为直径的圆的方程为 x2＋y2＝1， ∴圆心(0，0)到直线 l 的距离 d＝2|m| 5 . 由 d<1，得|m|< 5 2 ，(*) ∴|CD|＝2 1－d2＝2 1－4 5 m2＝ 2 5 5－4m2. 设 A(x1，y1)，B(x2，y2)， 由 y＝－1 2 x＋m， x2 4 ＋y2 3 ＝1 得 x2－mx＋m2－3＝0， 由根与系数的关系得 x1＋x2＝m，x1x2＝m2－3， ∴|AB|＝ 1＋ －1 2 2 [m2－4（m2－3）]＝ 15 2 4－m2. 由|AB| |CD| ＝5 3 4 ，得 4－m2 5－4m2＝1，解得 m＝± 3 3 ，满足(*)． ∴直线 l 的方程为 y＝－1 2 x＋ 3 3 或 y＝－1 2 x－ 3 3 . 21．解：（1）函数 ( )f x 的定义域为 2 11 ln (0 1) (1 ) ( ) ( 1) xxf x x      ， ， ， ， 令 1( ) 1 lng x xx    ，则有 2 1( ) xg x x   ， 令 2 1( ) 0xg x x    ，解得 1x  ，所以在 (0 1)， 上， ( ) 0g x  ， ( )g x 单调递增， 在 (1 ) ， 上， ( ) 0g x  ， ( )g x 单调递减． 又 (1) 0g  ，所以 ( ) 0g x ≤ 在定义域上恒成立．即 ( ) 0f x  在定义域上恒成立， 所以 ( )f x 在 (0 1)， 上单调递减，在 (1 ) ， 上单调递减． （2）由 ( ) exf x k≤ 在 (1 ) ， 上恒成立得： ln e1 xx kx  ≤ 在 (1 ) ， 上恒成立． 整理得： ln ( 1)e 0xx k x  ≤ 在 (1 ) ， 上恒成立. 令 ( ) ln ( 1)exh x x k x   ，易知，当 0k ≤ 时， ( ) 0h x ≤ 在 (1 ) ， 上恒成立不可能， 0k  ， 又 1( ) exh x kxx    ， (1) 1 eh k   ， 1°当 1 ek ≥ 时， (1) 1 e 0h k   ≤ ，又 1( ) exh x kxx    在 (1 ) ， 上单调递减，所以 ( ) 0h x ≤ 在 (1 ) ， 上恒成立，则 ( )h x 在 (1 ) ， 上单调递减，又 (1) 0h  ，所以 ( ) 0h x ≤ 在 (1 ) ， 上 恒成立． 2°当 10 ek  时， (1) 1 e 0h k    ， 11 e 0kh kk        ，又 1( ) exh x kxx    在 (1 ) ， 上单 调递减， 所以存在 0 (1 )x   ， ，使得 0( ) 0h x  ， 所以在 0(1 )x， 上 ( ) 0h x  ，在 0( )x  ， 上 ( ) 0h x  ， 所以 ( )h x 在 0(1 )x， 上单调递增，在 0( )x  ， 上单调递减， 又 (1) 0h  ，所以 ( ) 0h x  在 0(1 )x， 上恒成立， 所以 ( ) 0h x ≤ 在 (1 ) ， 上恒成立不可能． 综上所述， 1 ek ≥ ． 22.（1） （2） 23.（1） （2）