高中数学（人教A版）必修3能力强化提升及单元测试：1-2-3 7页

‎1.2.3　循环语句 双基达标　(限时20分钟) ‎1．下列的程序执行后输出的结果是 (　　)．‎ A．－1 B．0 C．1 D．2‎ 解析　当S＝5＋4＋3＋2＝14时，n＝2－1＝1，此时S<15继续执行循环体，则S＝5＋4‎ ‎＋3＋2＋1＝15，n＝1－1＝0，此时S＝15，循环结束，输出0.‎ 答案　B ‎2．在循环语句中，下列说法正确的是 (　　)．‎ A．UNTIL型循环可以无限循环 B．WHILE型循环可以无限循环 C．循环语句中必须有判断 D．WHILE型循环不能实现UNTIL型循环的功能 解析　UNTIL型循环和WHILE型循环实现的功能是一样的，只是看不同条件下哪种方 便而已．‎ 答案　C ‎3．下面的程序：‎ 执行完毕后a的值为 (　　)．‎ A．99 B．100 C．101 D．102‎ 解析　a＝99＋1＝100.‎ 答案　B ‎4．运行下面的程序，输出的值为________．‎ 解析　由于循环体是先执行S＝S＋i，再执行i＝i＋1，然后进行判断，当S＝1＋2＋3＋4＋5＝15时，执行i＝5＋1＝6，这时15＜18成立，再循环一次S＝15＋6＝21，i＝6＋1‎ ‎＝7，这时再判断21＜18不成立，于是执行“PRINT i”，即i＝7.‎ 答案　7‎ ‎5．下面的程序运行后第3个输出的数是________．‎ 解析　该程序中关键是循环语句，‎ 第一次输出的数是1，‎ 第二次输出的数是x＝1＋＝，‎ 第三次输出的数是x＝1＋＋＝2.‎ 答案　2‎ ‎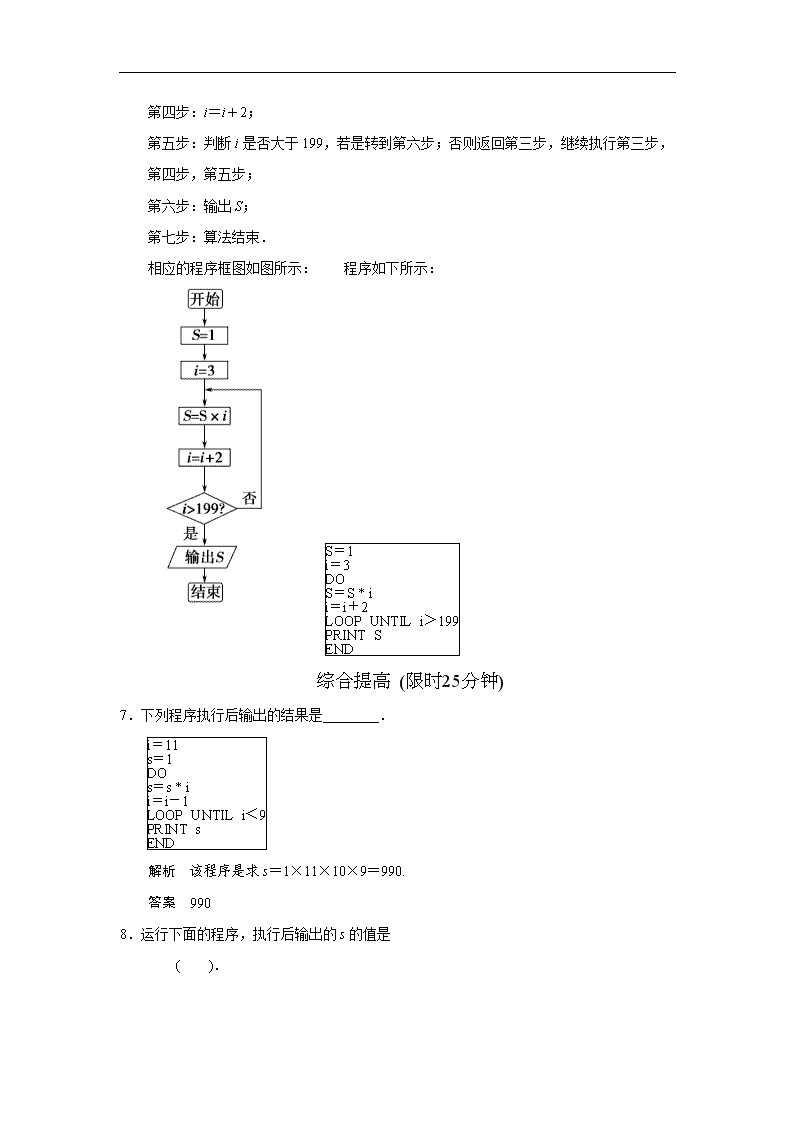6．设计一个计算1×3×5×7×…×199的算法，并写出程序，画出程序框图．‎ 解　算法步骤如下：‎ 第一步：S＝1；‎ 第二步：i＝3；‎ 第三步：S＝S×i；‎ 第四步：i＝i＋2；‎ 第五步：判断i是否大于199，若是转到第六步；否则返回第三步，继续执行第三步，‎ 第四步，第五步；‎ 第六步：输出S；‎ 第七步：算法结束．‎ 相应的程序框图如图所示：　　程序如下所示：‎ ‎　　 　　　 ‎7．下列程序执行后输出的结果是________．‎ 解析　该程序是求s＝1×11×10×9＝990.‎ 答案　990‎ ‎8．运行下面的程序，执行后输出的s的值是 (　　)．‎ A．11 B．15 C．17 D．19‎ 解析　当i＝3时，s＝7，当i＝5时，s＝11，‎ 此时仍满足条件“i＜6”，因此再循环一次，‎ 即i＝7时，s＝15，此时不满足“i＜6”，‎ 所以执行“PRINT s”，即s＝15.‎ 答案　B ‎9．运行下面的程序，输出的结果为________．‎ A＝1‎ B＝1‎ WHILE　B＜15‎ ‎　A＝A＋B ‎　B＝A＋B WEND C＝A＋B PRINT“C＝”；C END 解析　循环结构中，循环体的作用是将前两个数相加，得到后一个数；如果没有循环条件的限制，程序中的循环结构将依次给A，B赋值为：1,1,2,3,5,8,13,21,34，…‎ 其中第1,3,5，…个数为A的值，第2,4,6，…个数为B的值，可见B＝21时，循环结束，此时，A＝13，所以C＝A＋B＝34.‎ 答案　C＝34‎ ‎10．下列程序运行的结果为________．‎ i＝1‎ S＝0‎ WHILE　S＜＝20‎ ‎　S＝S＋i ‎　i＝i＋1‎ WEND PRINT　i END 解析　第一次循环：S＝0＋1＝1，i＝1＋1＝2；第二次循环：S＝1＋2＝3，i＝2＋1＝3；第三次循环：S＝3＋3＝6，i＝3＋1＝4；第四次循环：S＝6＋4＝10，i＝4＋1＝5；第五次循环：S＝10＋5＝15，i＝5＋1＝6；第六次循环：S＝15＋6＝21＞20，i＝6＋1＝7，故输出i的值为7.‎ 答案　7‎ ‎11．设计算法求＋＋＋…＋的值，并画出程序框图及编写程序．‎ 解　算法如下：‎ 第一步：令S＝0，i＝1；‎ 第二步：若i≤99成立，则执行第三步；‎ 否则，输出S，结束算法；‎ 第三步：S＝S＋；‎ 第四步：i＝i＋1，返回第二步．‎ 程序框图：‎ 法一　当型循环程序框图：　　程序如下：‎ S＝0‎ i＝1‎ WHILE i＜＝99‎ S＝S＋1/(i*(i＋1))‎ i＝i＋1‎ WEND PRINT　S END 法二　直到型循环程序框图：‎ S＝0‎ i＝1‎ DO S＝S＋1/(i*(i＋1))‎ i＝i＋1‎ LOOP UNTIL i＞99‎ PRINT　S END 程序如下：‎ ‎12．(创新拓展)某商场第一年销售计算机5 000台，如果平均每年销售量比上一年增加10%，那么从第一年起，大约几年可使总销售量达到30 000台？画出解决此问题的程序框图，并写出程序．‎ 解　程序框图如下图所示：‎ 程序：‎ m＝5 000‎ S＝0‎ i＝0‎ WHILE　S＜30 000‎ S＝S＋m m＝m*(1＋0.1)‎ i＝i＋1‎ WEND PRINT　i END