高中数学选修2-2教学课件4_5_4_1《微积分基本定理（第1课时）》 23页

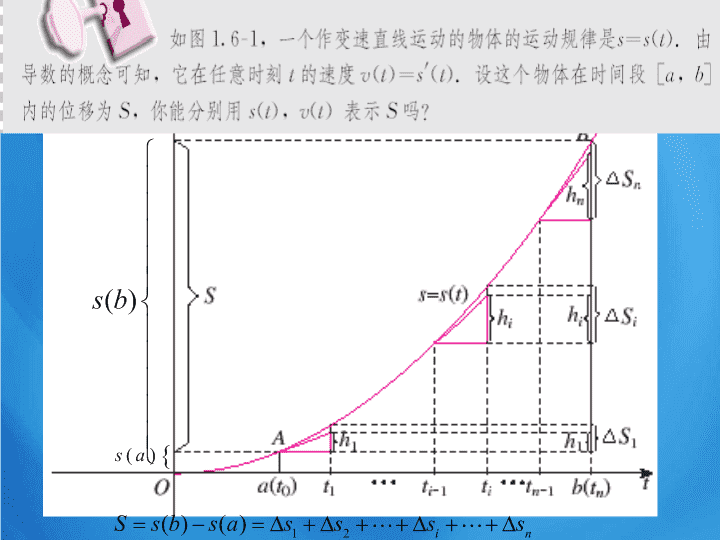
4.5.4.1 微积分基本定理 ( 一） 1. 由定积分的定义可以计算 , 但比较麻烦 ( 四步曲 ), 有没有更加简便有效的方法求定积分呢 ? 引入 引例小结： 在变速直线运动中 , 已知位置函数 与速度函数 之间有关系 : 物体在时间间隔 内经过的路程为 这种积分与原函数的关系在一定条件下具有普遍性 . 定理 （微积分基本定理） 二、牛顿 — 莱布尼茨公式 如果 f(x) 是区间 [a,b] 上的连续函数 , 并且 F ’ (x)=f(x), 则 注意 : 3. 牛顿－莱布尼茨公式沟通了导数与积分之间的关系． 例 1 计算下列定积分 解 （１） ∵ 找出 f(x) 的一个原函数是关键 练习： 1 1/2 1/4 15/4 复习 : 定积分的基本性质 性质 1. 性质 2. 例 ２．计算下列定积分 原式 解 :∵ 练习： =29/6 =1 =9 =e 2 -e+1 例 ３．计算下列定积分 解 （ 1 ） ∵ 思考 : 0 1 解 思考 : 0 0 微积分基本公式 三、小结 牛顿－莱布尼茨公式沟通了导数与定积分之间的关系． F’(x)=f(x) 本讲到此结束，请同学们课后再做好复习 . 谢谢！ 再见！ 作业 P71 拓展：积分上限的函数及其导数 则变上限函数 证 : 则有 定理 1. 若 例 1. 证明 在 内为单调递增函数 . 证 : 只要证 拓展：牛顿 – 莱布尼茨公式 （高等数学推导方法） ( 牛顿 - 莱布尼茨公式 ) 证 : 根据定理 1, 故 因此 得 记作 定理 2. 函数 , 则 或 例 2. 计算 解 : 例 3. 计算正弦曲线 的面积 . 解 : 例 4. 汽车以每小时 36 km 的速度行驶 , 速停车 , 解 : 设开始刹车时刻为 则此时刻汽车速度 刹车后汽车减速行驶 , 其速度为 当汽车停住时 , 即 得 故在这段时间内汽车所走的距离为 刹车 , 问从开始刹 到某处需要减 设汽车以等加速度 车到停车走了多少距离 ? 备用题 解 ： 1. 设 求 定积分为常数 , 设 , 则 故应用积分法定此常数 . 拓展部分内容小结 则有 1. 微积分基本公式 积分中值定理 微分中值定理 牛顿 – 莱布尼茨公式 2. 变限积分求导公式