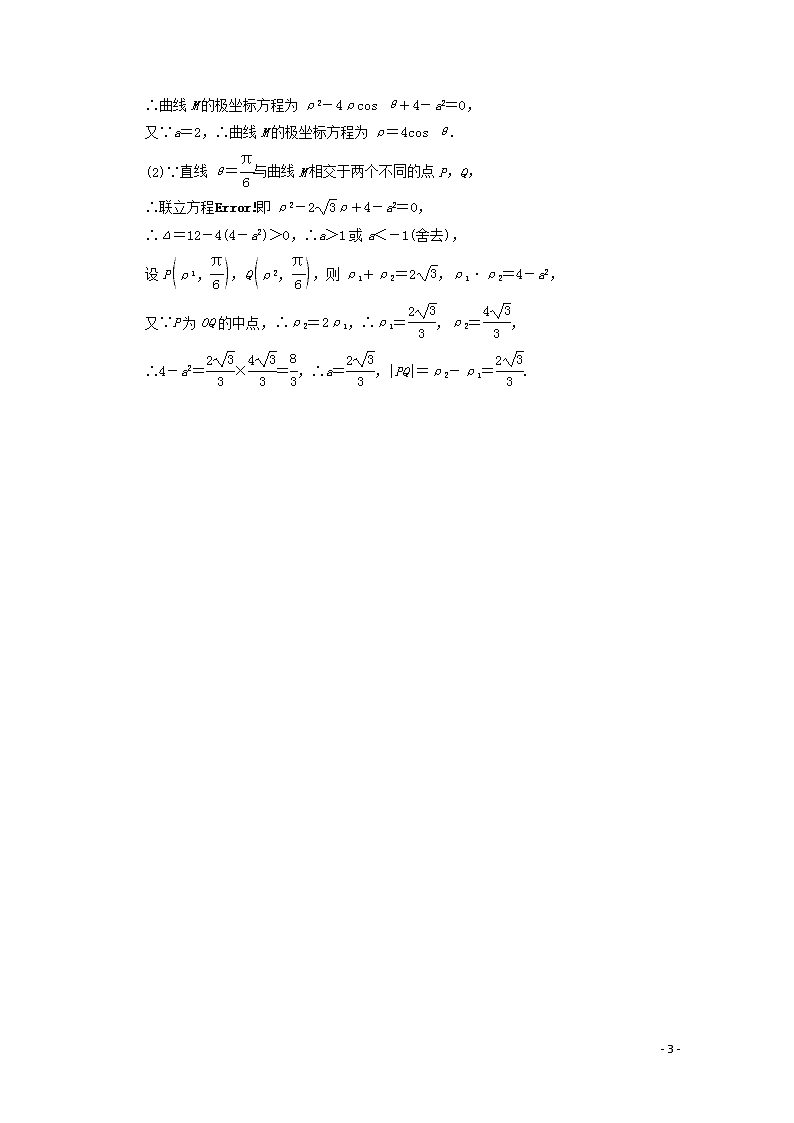2021高考数学一轮复习课后限时集训66坐标系文北师大版2 3页

课后限时集训66‎ 坐标系 建议用时：45分钟 ‎1．在直角坐标系xOy中，曲线C的方程为(x－3)2＋(y－4)2＝25.以坐标原点O为极点，x轴正半轴为极轴建立极坐标系．‎ ‎(1)求曲线C的极坐标方程；‎ ‎(2)设l1：θ＝，l2：θ＝，若l1，l2与曲线C分别交于异于原点的A，B两点，求△AOB的面积．‎ ‎[解](1)∵曲线C的普通方程为(x－3)2＋(y－4)2＝25，即x2＋y2－6x－8y＝0.‎ ‎∴曲线C的极坐标方程为ρ＝6cos θ＋8sin θ.‎ ‎(2)设A，B.‎ 把θ＝代入ρ＝6cos θ＋8sin θ，‎ 得ρ1＝4＋3，‎ ‎∴A.‎ 把θ＝代入ρ＝6cos θ＋8sin θ，‎ 得ρ2＝3＋4，‎ ‎∴B.‎ ‎∴S△AOB＝ρ1ρ2sin∠AOB ‎＝(4＋3)(3＋4)sin ‎＝12＋.‎ ‎2．在极坐标系中，已知圆C经过点P，圆心为直线ρsin＝－与极轴的交点，求圆C的极坐标方程．‎ ‎[解]　在ρsin＝－中，‎ 令θ＝0，得ρ＝1，‎ 所以圆C的圆心坐标为(1,0)．‎ 因为圆C经过点P，‎ - 3 -‎ 所以圆C的半径|PC|＝＝1，于是圆C过极点，所以圆C的极坐标方程为ρ＝2cos θ.‎ ‎3．(2019·哈尔滨模拟)以直角坐标系原点O为极点，x轴正半轴为极轴，已知曲线C1的方程为(x－1)2＋y2＝1，C2的方程为x＋y＝3，C3是一条经过原点且斜率大于0的直线．‎ ‎(1)求C1与C2的极坐标方程；‎ ‎(2)若C1与C3的一个公共点为A(异于点O)，C2与C3的一个公共点为B，求|OA|－的取值范围．‎ ‎[解](1)曲线C1的方程为(x－1)2＋y2＝1，C1的极坐标方程为ρ＝2cos θ，‎ C2的方程为x＋y＝3，其极坐标方程为ρ＝，‎ ‎(2)C3是一条过原点且斜率为正值的直线，C3的极坐标方程为θ＝α，α∈，‎ 联立C1与C3的极坐标方程得ρ＝2cos α，‎ 即|OA|＝2cos α.‎ 联立C2与C3的极坐标方程得 ρ＝，即|OB|＝，‎ 所以|OA|－＝2cos α－cos α－sin α＝cos，‎ 又α∈，所以|OA|－∈(－1,1)．‎ ‎4．在以极点为原点，极轴为x轴正半轴的直角坐标系中，曲线C的参数方程为(a＞0且a≠1，θ为参数)，将曲线C上每一点的横坐标不变，纵坐标变为原来的a倍，得到曲线M.‎ ‎(1)若a＝2，求曲线M的极坐标方程；‎ ‎(2)若直线θ＝与曲线M相交于两个不同的点P，Q，且P为OQ的中点，求a的值及|PQ|的值．‎ ‎[解](1)设(x，y)为曲线M上的任意一点，其在曲线C上相应点的坐标为(x′，y′)，‎ 由题意得即 ‎∵∴ 即消去参数θ得曲线M的普通方程为(x－2)2＋y2＝a2，即x2＋y2－4x＋4＝a2，‎ ‎∴曲线M的极坐标方程为ρ2－4ρcos θ＋4－a2＝0，‎ 又∵a＝2，∴曲线M的极坐标方程为ρ＝4cos θ.‎ - 3 -‎ ‎(2)∵直线θ＝与曲线M相交于两个不同的点P，Q，‎ ‎∴联立方程即ρ2－2ρ＋4－a2＝0，‎ ‎∴Δ＝12－4(4－a2)＞0，∴a＞1或a＜－1(舍去)，‎ 设P，Q，则ρ1＋ρ2＝2，ρ1·ρ2＝4－a2，‎ 又∵P为OQ的中点，∴ρ2＝2ρ1，∴ρ1＝，ρ2＝，‎ ‎∴4－a2＝×＝，∴a＝，|PQ|＝ρ2－ρ1＝.‎ - 3 -‎