数学理·四川省巴中市高中2017届高三毕业班10月零诊考试理数试题 Word版含解析 19页

全*品*高*考*网， 用后离不了！‎ 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1.已知全集，集合，，则图中阴影部分所表示的集合为（ ）‎ A． B． C． D． ‎ ‎【答案】A.‎ ‎【解析】‎ 试题分析：由图可知，，故选A.‎ 考点：集合的运算.‎ ‎2.设，，若：，：，则是的（ ）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎ ‎【答案】D.‎ 考点：1.不等式的性质；2.充分必要条件.‎ ‎3.设为虚数单位，则的展开式中含的项为（ ）‎ A． B． C． D． ‎【答案】A.‎ ‎【解析】‎ 试题分析：由二项展开的通项公式，令，故的系数是，故选A.‎ 考点：1.二项式定理；2.复数的计算.‎ ‎4.若坐标原点到抛物线的准线的距离为2，则（ ）‎ A．8 B． C． D． ‎【答案】D.‎ ‎【解析】‎ 试题分析：将其化为标准方程：，∴，故选D.‎ 考点：抛物线的标准方程及其性质.‎ ‎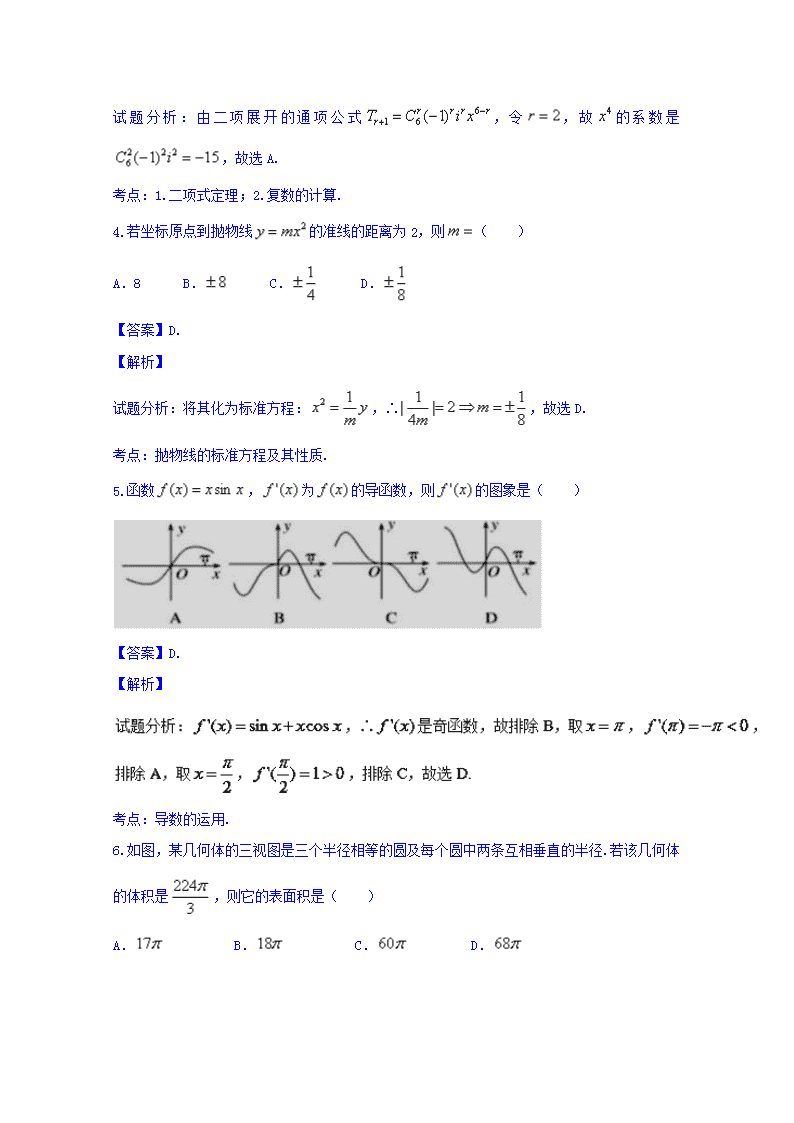5.函数，为的导函数，则的图象是（ ）‎ ‎【答案】D.‎ ‎【解析】‎ 考点：导数的运用.‎ ‎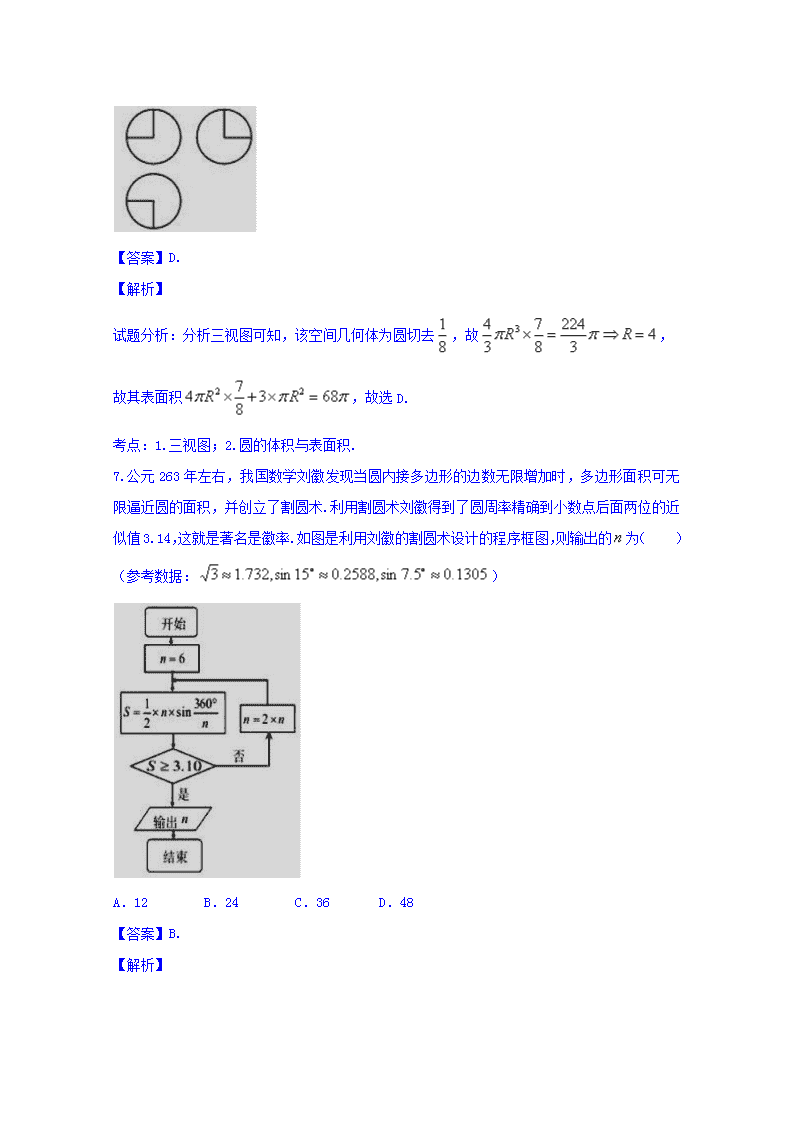6.如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是，则它的表面积是（ ）‎ A． B． C． D． ‎【答案】D.‎ ‎【解析】‎ 试题分析：分析三视图可知，该空间几何体为圆切去，故，‎ 故其表面积，故选D.‎ 考点：1.三视图；2.圆的体积与表面积.‎ ‎7.公元263年左右，我国数学刘徽发现当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了割圆术.利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名是徽率.如图是利用刘徽的割圆术设计的程序框图，则输出的为（ ）‎ ‎（参考数据：）‎ A．12 B．24 C．36 D．48‎ ‎【答案】B.‎ ‎【解析】‎ 考点：1.三角函数；2.程序框图.‎ ‎8.设，为空间两条不同的直线，，为空间两个不同的平面，给出下列命题：‎ ‎①若，，则； ②若，，则；‎ ‎③若，，则；④若，，则.‎ 其中所有正确命题的序号是（ ）‎ A．③④ B．②④ C．①② D．①③‎ ‎【答案】A.‎ ‎【解析】‎ 试题分析：根据线面平行的性质可知①②错误，根据线面垂直的性质可知③④正确，故选A.‎ 考点：1.线面平行的性质；2.线面平行的性质. ‎ ‎9.已知函数，则下列结论正确的是（ ）‎ A．导函数为 ‎ B．函数的图象关于直线对称 ‎ C．函数在区间上是增函数 ‎ D．函数的图象可由函数的图象向右平移个单位长度得到 ‎ ‎【答案】C.‎ ‎【解析】‎ 考点：的图象和性质.‎ ‎【名师点睛】根据，的图象求解析式的步骤：1.首先确定振幅和周期，从而得到与；2.求的值时最好选用最值点求：峰点：，谷点：，‎ 也可用零点求，但要区分该零点是升零点，还是降零点，升零点(图象上升时与轴的交点)：；降零点(图象下降时与轴的交点)：(以上)．‎ ‎10.在中，角，，的对边分别为，，，且，若的面积，则的最小值为（ ）‎ A． B． C． D．3‎ ‎【答案】B.‎ ‎【解析】‎ 考点：1.三角恒等变换与解三角形；2.不等式求最值. ‎ ‎【思路点睛】在判断三角形的形状时，一般将已知条件中的边角关系利用正弦定理或余弦定理转化为角角关系(注意应用这个结论)或边边关系，‎ 再用三角变换或代数式的恒等变形(如因式分解、配方等)求解.‎ ‎11.定义在上的奇函数和偶函数满足：，给出如下结论：‎ ‎①且； ‎ ‎②，总有；‎ ‎③，总有；‎ ‎④，使得.‎ 其中所有正确结论的序号是（ ）‎ A．①②③ B．②③ C．①③④ D．①②③④‎ ‎【答案】A.‎ ‎【解析】‎ 试题分析：由题意得，，①：，故①正确；②：，故②正确；③：，故③正确；④：，故④错误，即正确的结论为①②③，故选A.‎ 考点：函数的性质.‎ ‎12.已知函数，方程有四个实数根，则的取值范围为（ ）‎ ‎ A． B． C． D． ‎【答案】A.‎ ‎【解析】‎ ‎ ‎ 考点：函数与方程.‎ ‎【方法点睛】运用函数图象结合数形结合思想求解问题的类型：1.对一些可通过平移、对称变换作出其图像的对数型函数，在求解其单调性(单调区间)、值域(最值)、零点时，常利用数形结合思想；2.一些函数型方程、不等式问题常转化为相应的函数图像问题，利用数形结合法求解．‎ 二、填空题（本大题共4小题，每小题5分，共20分．）‎ ‎13.已知向量与共线且方向相同，则 .‎ ‎【答案】. ‎ 考点：向量的共线坐标表示.‎ ‎14.若，则 .‎ ‎【答案】. ‎ ‎【解析】‎ 试题分析：由题意得，或，∴或，∴，故填：.‎ 考点：对数的运算.‎ ‎15.正月十六登高是“中国石刻艺术之乡”、“中国民间文化艺术之乡”四川省巴中市沿袭千年的独特民俗.登高节前夕，李大伯在家门前的树上挂了两串喜庆彩灯，这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后，它们第一次闪亮的时刻相差不超过2秒的概率是 .‎ ‎【答案】. ‎ ‎【解析】‎ 考点：几何概型.‎ ‎【思路点睛】1.以面积为度量的几何概型概率计算公式：，其中为事件构成区域的面积，为整个试验的全部结果构成区域的面积；2.解此类问题的主要步骤为：列出条件组，画出图形，计算面积，再求概率；3.多注意数形结合.‎ ‎16.设函数，其中，，若存在使得成立，则实数的值是 . ‎ ‎【答案】. ‎ ‎【解析】‎ 考点：1.导数的综合运用；2.数形结合的数学思想； 3.转化的数学思想.‎ ‎【思路点睛】此类综合题常考虑的方面：1.考虑函数的定义域，保证研究过程有意义；2.弄清常见函数的单调区间；3.函数结构形似联想与几何意义；4.注意恒成立与存在性不等式的等价转化问题．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤） ‎ ‎17.(本小题满分12分)在等差数列中，，.‎ ‎（1）求数列的通项公式； ‎ ‎（2）设数列是首项为，公比为的等比数列，求的前项和.‎ ‎【答案】（1）；（2）详见解析.‎ ‎【解析】‎ 考点：1.等差数列，等比数列的通项公式及其前项和；2.分类讨论的数学思想 ‎18.(本小题满分12分)某中学举行了一次“环保知识竞赛”活动. 为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数(得分取正整数，满分为100分)作为样本(样本容量为)进行统计. 按照的分组作出频率分布直方图，并作出样本分数的茎叶图(图中仅列出了得分在的数据).‎ ‎（1）求样本容量和频率分布直方图中的，的值； ‎ ‎（2）在选取的样本中，从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动，设表示所抽取的3名同学中得分在[80,90)的学生人数，求的分布列及数学期望.‎ ‎【答案】（1），；（2）详见解析.‎ ‎【解析】‎ ‎∴的分布列为 ‎1‎ ‎2‎ ‎3‎ ‎∴.‎ 考点：1.频率分布直方图；2.古典概型及离散型随机变量分布列的求法.‎ ‎19. (本小题满分12分)如图，在直三棱柱中，是的中点.‎ ‎（1）求证：平面；‎ ‎（2）若，，，求平面与平面所成二面角的正弦值.‎ ‎【答案】（1）详见解析；（2）.‎ ‎【解析】‎ 易得平面的法向量为，故，‎ 故平面与平面所成二面角的正弦值为.‎ 考点：1.线面平行的判定；2.二面角的求解. ‎ ‎20. (本小题满分12分) 已知椭圆：()的一个焦点为，左右顶点分别为，经过点的直线与椭圆交于两点.‎ ‎（1）求椭圆方程； ‎ ‎（2）记与的面积分别为和，求的最大值.‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎ ，由可得，当且仅当时等号成立，∴的最大值为.‎ 考点：1.椭圆的标准方程；2.椭圆中的最值问题.‎ ‎【方法点睛】求解范围问题的常见求法：（1）利用判别式来构造不等关系，从而确定参数的取值范围；（2）利用已知参数的范围，求新参数的范围，解这类问题的核心是在两个参数之间建立等量关系；（3）利用隐含或已知的不等关系建立不等式，从而求出参数的取值范围；（4）利用基本不等式求出参数的取值范围；（5）利用函数的值域的求法，确定参数的取值范围．‎ ‎21. (本小题满分12分)已知函数在处取得极值.‎ ‎（1）求的值； ‎ ‎（2）若对任意的，都有成立(其中是函数的导函数)，求实数的最小值；‎ ‎（3）证明：().‎ ‎【答案】（1），；（2）；（3）详见解析.‎ ‎【解析】‎ ‎（2）由（1）得，∴，∴在上恒成立，即在上恒成立，设，则，‎ ，，设，‎ 考点：1.导数的综合运用；2.等价转化的数学思想.‎ ‎【思路点睛】1.可导函数在某点处取得极值的充要条件；2.用求导法、分类讨论思想探寻恒成立有关的逆向求参问题；3.用特殊赋值法构造“零件”不等式，然后通过叠加、放缩证明难度较大的数列不等式.‎ 请考生在第22、23题中任意选一题作答。如果多做，则按所做第一题记分。‎ ‎22.（本小题满分10分）选修4-4：坐标系与参数方程 在平面直角坐标系中，以为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，曲线的参数方程为（为参数）.‎ ‎（1）求曲线的直角坐标方程和曲线的普通方程；‎ ‎（2）当曲线和曲线有两个不同公共点时，求实数的取值范围.‎ ‎【答案】（1）详见解析；（2）.‎ ‎【解析】‎ 考点：1.极坐标、参数方程与普通方程的互化；2.直线与圆的位置关系.‎ ‎23.（本小题满分10分）选修4-5：不等式选讲 已知函数，不等式的解集为.‎ ‎（1）求实数的值；‎ ‎（2）若关于的不等式恒成立，求实数的取值范围.‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ 试题分析：（1）利用绝对值的性质，解含参的绝对值不等式，再根据解集是即可求解，；（2）分析题意，问题等价于恒成立，利用绝对值的几何意义即可求解.‎ 试题解析：（1）∵，∴不等式，即，∴，‎ 而不等式的解集为，∴且，解得；（2）由（1），‎ 关于的不等式恒成立关于的不等式恒成立 恒成立，而，∴只需 ，‎ 则或，解得或，故实数的取值范围为.‎ 考点：1.绝对值不等式；2.恒成立问题．‎ ‎ ‎ ‎ ‎