2020届二轮复习用样本的频率分布估计总体分布(第课时)课件（18张）（全国通用） 18页

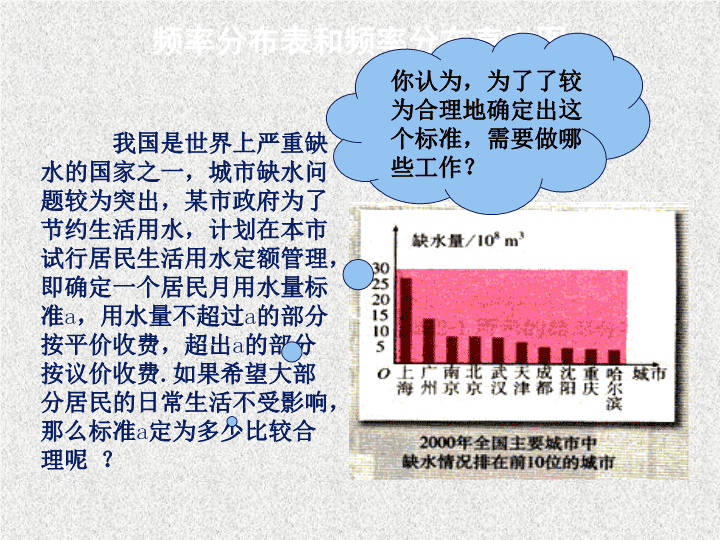
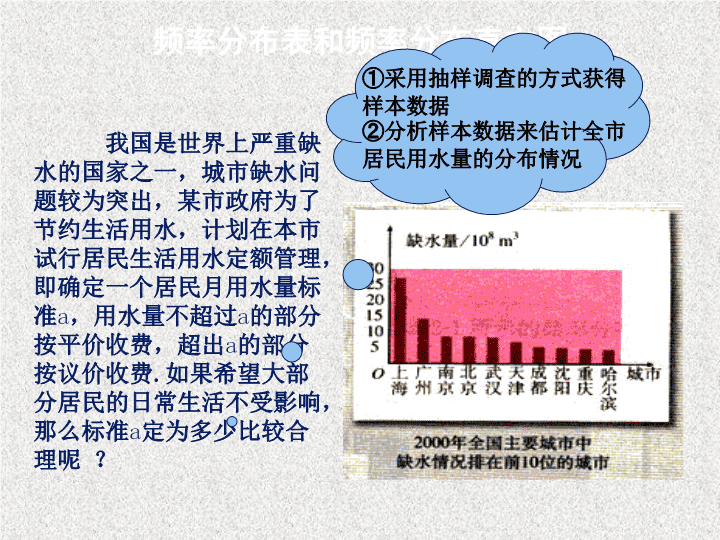
问题提出 1.随机抽样有哪几种基本的抽样方法？ 2.随机抽样是收集数据的方法，如何通 过样本数据所包含的信息，估计总体的 基本特征，即用样本估计总体，是我们 需要进一步学习的内容. 简单随机抽样、系统抽样、分层抽样. 我国是世界上严重缺 水的国家之一，城市缺水问 题较为突出，某市政府为了 节约生活用水，计划在本市 试行居民生活用水定额管理， 即确定一个居民月用水量标 准a，用水量不超过a的部分 按平价收费，超出a的部分 按议价收费.如果希望大部 分居民的日常生活不受影响， 那么标准a定为多少比较合 理呢 ？ 频率分布表和频率分布直方图 你认为，为了了较 为合理地确定出这 个标准，需要做哪 些工作？ 频率分布表和频率分布直方图 我国是世界上严重缺 水的国家之一，城市缺水问 题较为突出，某市政府为了 节约生活用水，计划在本市 试行居民生活用水定额管理， 即确定一个居民月用水量标 准a，用水量不超过a的部分 按平价收费，超出a的部分 按议价收费.如果希望大部 分居民的日常生活不受影响， 那么标准a定为多少比较合 理呢 ？ ①采用抽样调查的方式获得 样本数据 ②分析样本数据来估计全市 居民用水量的分布情况 下表给出100位居民的月均用水量表 分析数据的一种基本方法是用图将它们画出来，或者用紧凑的 表格改变数据的排列方式，作图可以达到两个目的，一是从数 据中提取信息，二是利用图形传递信息.表格则是通过改变数 据的构成形式，为我们提供解释数据的新方式. 讨论：如何分 析数据？ 根据这些数据 你能得出用水 量其他信息吗 ? 为此我们要对这些数据进行整理与分析 〈一〉频率分布的概念： 频率分布是指一个样本数据在各个小 范围内所占比例的大小.一般用频率分 布直方图反映样本的频率分布. 〈二〉画频率分布直方图其一般步骤为 （1）计算一组数据中最大值与最小值的差， 即求极差 （2）决定组距与组数 （3）将数据分组 （4）列频率分布表 （5）画频率分布直方图 第一步: 求极差:(数据组中最大值与最小值的差距) 最大值 = 4.3 最小值 = 0.2 所以极差 = 4.3 - 0.2 = 4.1 第二步: 决定组距与组数:（强调取整） 当样本容量不超过100时,按照数据的多少,常分成5-12组. 为方便组距的选择应力求“取整”. 本题如果组距为0.5(t). 则 所以将数据分成9组较合适. 第三步: 将数据分组：(给出组的界限) [0, 0.5), [0.5, 1), [1, 1.5),…[4, 4.5)共9组. 第四步: 列频率分布表. 分组 频数 频率 频率/组距 [0-0.5) 4 [0.5-1) 8 [1-1.5) 15 [1.5-2) 22 [2-2.5) 25 [2.5-3) 15 [3-3.5) 5 [3.5-4) 4 [4-4.5) 2 合计 100 组距 = 0.5 0.04 0.08 0.08 0.16 0.300.15 0.440.22 0.25 0.50 2.00 0.02 0.04 0.04 0.08 0.10 0.300.15 0.05 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.5 1 1.5 2 2.5 3 3.5 4 4.5 第五步: 画出频率分布直方图. 频率/组距 月均用水量/t (组距 = 0.5) 0.08 0.16 0.3 0.44 0.5 0.3 0.1 0.08 0.04 小长方形的面 积=? 小长方形的面 积总和=? 月均用水量最 多的在哪个区 间? 请大家阅读第 68页,直方图有 哪些优点和缺 点? 频率分布直方图的特征： 从频率分布直方图可以清楚的看出数 据分布的总体趋势. 从频率分布直方图得不出原始的数据 内容，把数据表示成直方图后，原有 的具体数据信息就被抹掉了. 思考1：频率分布表与频率分布直方图的 区别？ 频率分布表列出的是在各个不同区间内取 值的频率. 频率分布直方图是用小长方形面积的大小 来表示在各个区间内取值的频率. 思考2：如果当地政府希望使85%以上的居民 每月的用水量不 超出标准，根据频率分布表2-2和频率分布直 方图2.2-1， 你能对制定月用水量标准（即a的取值）提出 建议吗？ 88%的居民月用水量在3t以下， 可建议取a=3. 思考3：将组距确定为1，作出教材P66页 居民月 均用水量的频率分布直方图. 频率 组距 月均用水量/t 0.4 0.3 0.2 0.1 1 2 3 4 5 O 思考4：谈谈两种组距下，你对图的印象 ？同一个样本数据，绘制出来的分布图是 唯一的吗？ （同样一组数据，如果组距不同，横轴、纵 轴的单位不同，得到的图和形状也会不同. 不同的形状给人以不同的印象，这种印象有 时会影响我们对总体的判断 .） 1.有一个容量为50的样本数据的分组的频数如下： ［12.5, 15.5） 3 ［15.5, 18.5） 83 ［18.5, 21.5） 9 ［21.5, 24.5） 11 ［24.5, 27.5） 10 ［27.5, 30.5） 5 ［30.5, 33.5） 4 (1)列出样本的频率分布表; (2)画出频率分布直方图; (3)根据频率分布直方图估计,数据落在[15.5, 24.5）的百分比是多少? 理论迁移 解: 分组 频数 频率 频率/ 组距 ［12.5, 15.5） 3 0.06 0.020 ［15.5, 18.5） 8 0.16 0.053 ［18.5, 21.5） 9 0.18 0.060 ［21.5, 24.5） 11 0.22 0.073 ［24.5, 27.5） 10 0.20 0.067 ［27.5, 30.5） 5 0.10 0.033 ［30.5, 33.5） 4 0.08 0.027 频率分布直方图如下： 频率 组距 0.010 0.020 0.030 0.040 0.050 12.5 0.060 0.070 24.5O 18.5 30.5 33.5 2.投掷一枚均匀骰子44次的记录是： 3 2 4 1 5 1 3 4 5 6 5 4 2 5 3 1 3 4 1 4 5 1 6 3 3 1 2 4 2 6 3 4 6 6 1 6 2 2 5 2 6 5 4 3 现对这些数据进行整理，试画出频数分布直方图．　 第一步：写出样本可能出现的一切数值，即： 1,2,3,4,5,6 共6个数．(数据分组) 第二步：列出频率分布表： 样本 １ ２ ３ ４ ５ ６ 频数 7 7 8 8 7 7 频率 0.16 0.16 0.18 0.18 0.16 0.16 第三步: 画频率分布直方图 组距 = 1 频率 组距 0.15 0.16 0.17 1 0.18 3O 2 4 5 6 点数