江苏省南通市第一中学2019-2020学年高一上学期期中考试数学试题 19页

www.ks5u.com ‎2019—2020学年度南通一中高一年级第一学期中抽测 数学试题 一、选择题（本大题共12小题，每小题4分，共48分．在每小题给出的四个选项中，只有一个选项是符合题目要求的.）‎ ‎1.若集合，，则（）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 先计算集合M，N，再计算.‎ ‎【详解】集合，‎ ‎∵，，‎ ‎∴.‎ 故答案选C ‎【点睛】本题考查集合的并集与一元二次不等式的解法，考查运算求解能力，属于基础题型.‎ ‎2.扇形周长为6cm，面积为2cm2，则其圆心角的弧度数是（ ）‎ A. 1或5 B. 1或2 C. 2或4 D. 1或4‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 利用扇形弧长和面积计算公式完成求解.‎ ‎【详解】设扇形的半径为cm，圆心角为，则解得或 故选：D.‎ ‎【点睛】扇形的弧长和面积计算公式：‎ 弧长公式：；面积公式：，其中是扇形圆心角弧度数，是扇形的半径.‎ ‎3.函数的定义域为（）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 分别计算两部分的定义域，求交集得到答案.‎ ‎【详解】函数 ‎∵，∴.‎ 故答案选B ‎【点睛】本题考查函数的定义域，考查运算求解能力 ‎4.已知函数是幂函数，且其图象与两坐标轴都没有交点，则实数　　‎ A. B. 2 C. 3 D. 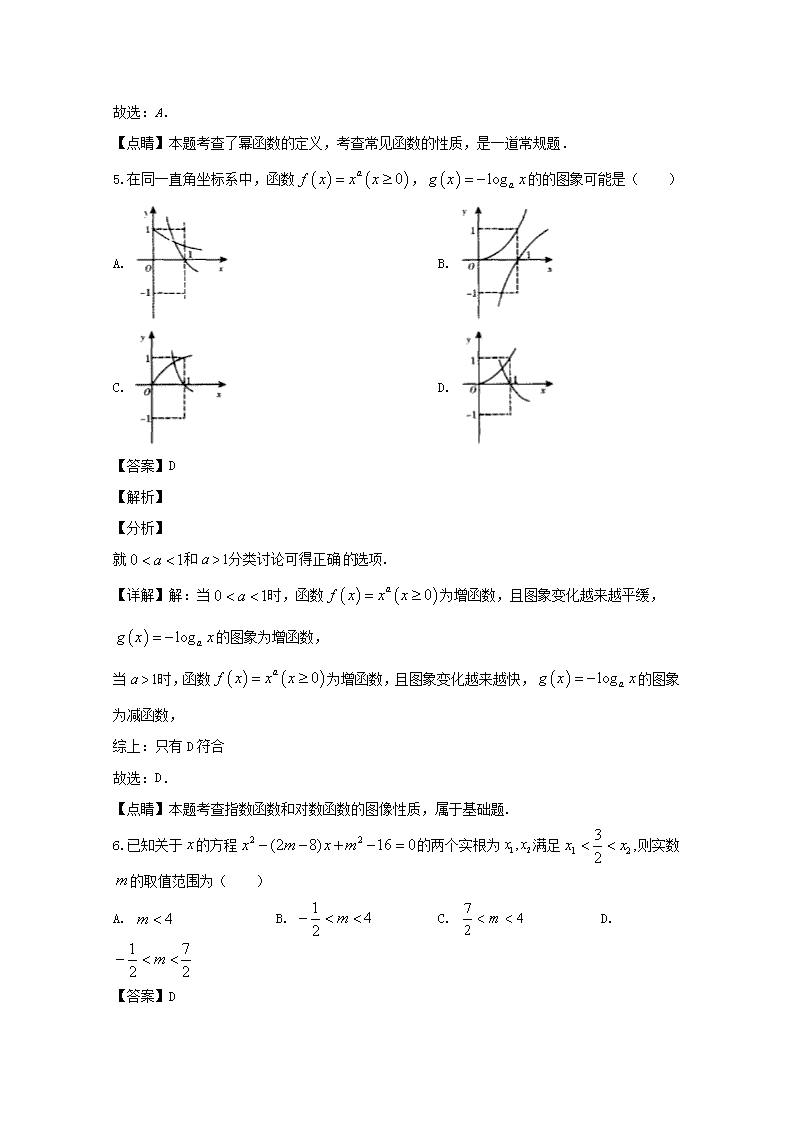2或 ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据幂函数的定义，求出m的值，代入判断即可．‎ ‎【详解】函数是幂函数，‎ ‎，解得：或，‎ 时，，其图象与两坐标轴有交点不合题意，‎ 时，，其图象与两坐标轴都没有交点，符合题意，‎ 故，‎ 故选：A．‎ ‎【点睛】本题考查了幂函数的定义，考查常见函数的性质，是一道常规题．‎ ‎5.在同一直角坐标系中，函数，的的图象可能是（　　）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 就和分类讨论可得正确选项.‎ ‎【详解】解：当时，函数为增函数，且图象变化越来越平缓，‎ 的图象为增函数，‎ 当时，函数为增函数，且图象变化越来越快，的图象为减函数，‎ 综上：只有D符合 故选：D．‎ ‎【点睛】本题考查指数函数和对数函数的图像性质，属于基础题.‎ ‎6.已知关于的方程的两个实根为满足则实数的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 利用二次方程实根分布列式可解得.‎ ‎【详解】设,‎ 根据二次方程实根分布可列式:,即,‎ 即,解得:.‎ 故选D.‎ ‎【点睛】本题考查了二次方程实根分布.属基础题.‎ ‎7.设集合，，则集合M与N的关系是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 将集合和集合整理后可知集合表示的奇数倍的角，集合表示的整数倍的角，从而得到集合之间的包含关系.‎ ‎【详解】‎ 表示所有奇数；表示所有整数 ‎ 本题正确选项：‎ ‎【点睛】本题考查集合间的包含关系，关键是能够将两个集合所表示的角的大小确定，从而得到包含关系.‎ ‎8.已知函数是奇函数，是偶函数，则（）‎ A. B. C. D. 3‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 利用奇函数的性质，可以求出的值，由偶函数的性质，可以求出的值，利用对数的运算公式，可以求出的值.‎ ‎【详解】因为函数是奇函数，所以，即，‎ 因为是偶函数，所以，‎ 因此，故本题选A.‎ ‎【点睛】本题考查了奇偶函数的性质，考查了对数的运算，考查了数学运算能力.‎ ‎9.设函数对的一切实数均有，则（ ）‎ A. － B. 2017 C. 2018 D. 4036‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 将x换成再构造一个等式，然后消去f（），得到f（x）的解析式，最后可求得f（2019）．‎ ‎【详解】∵f（x）+2f（）＝6x①‎ ‎∴f（）+2f（x）②‎ ‎∴①﹣②×2得﹣3f（x）＝6x ‎∴f（x）＝﹣2x，‎ ‎∴f（2019）＝﹣4038+4＝﹣4034.‎ 故选：A．‎ ‎【点睛】本题考查了函数解析式的求法，属中档题．‎ ‎10.已知为角的终边上的一点，且，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 利用三角函数的定义列方程，解方程求得的值，进而求得的值，将所求表达式转化为只含的形式，由此求得表达式的值.‎ ‎【详解】因为，故由正弦函数的定义可得，解得或(舍去),所以，所以，故选B.‎ ‎【点睛】本小题主要考查三角函数的定义，考查同角三角函数的基本关系式，考查齐次方程的运算，考查化归与转化的数学思想方法，属于中档题.‎ ‎11.已知单调函数的定义域为，对于定义域内任意，，则函数的零点所在的区间为（）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据单调性的性质和零点存在定理，可以求解出函数的零点所在的区间，选出正确答案.‎ ‎【详解】因为函数是定义域为上的单调函数，，所以 为一定值，设为，即，而，解得，因此，所以，‎ ‎，故函数的零点所在的区间为，本题选D.‎ ‎【点睛】本题考查了单调函数的性质，考查了零点存在定理，考查了换元法，对数式正负性的判断是解题的关键.‎ ‎12.已知函数,若对任意使得成立，则实数的取值范围为（　　）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 问题转化为对任意的使得恒成立，令，，根据函数的单调性求出的最小值，从而可得结果．‎ ‎【详解】对任意的使得成立，‎ 即对任意的使得恒成立，‎ 令，，‎ 显然在递增，‎ 故的最小值为，‎ 故，，‎ 实数的取值范围为,故选D．‎ ‎【点睛】本题主要考查指数函数的单调性的应用，以及不等式恒成立问题，属于中档题．不等式恒成立问题常见方法：① 分离参数恒成立(即可)或恒成立（即可）；② 数形结合( 图象在 上方即可)；③ 讨论最值或恒成立；④ 讨论参数，排除不合题意的参数范围，筛选出符合题意的参数范围.‎ 二、填空题（本大题共4小题，每小题5分，共20分．）‎ ‎13.函数的单调递增区间为______.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 先求得函数的定义域,再结合复合函数单调性的性质即可求得单调递增区间.‎ ‎【详解】由对数函数真数大于0,可得 ‎,解得 函数是由对数与二次函数的复合函数构成,由”同增异减”的单调性质,可知对数部分为单调递减函数,则二次函数部分为单调递减函数即可 二次函数单调递减区间是 结合函数定义域,所以整个函数单调递减区间为 ‎【点睛】本题考查了复合函数单调性的判断,注意对数函数对定义域的特殊要求.‎ ‎14.已知，当时，其值域________‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 令，因为，所以，得到函数 ‎，利用二次函数的性质，即可求解，得到答案．‎ ‎【详解】由题意，令，因为，所以，‎ 则函数，‎ 所以当时，函数取得最小值，最小值为，‎ 当时，函数取得最大值，最小值为，‎ 所以函数的值域为，‎ 故答案为．‎ ‎【点睛】本题主要考查了指数函数的性质，以及二次函数的图象与性质的应用，着重考查了换元思想，以及推理与运算能力，属于基础题．‎ ‎15.已知定义在上的函数满足，且函数在上是减函数，若，则的大小关系为__________．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 先判断函数的奇偶性，再分析得到，由函数单调性得到，即得解.‎ ‎【详解】，是偶函数，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 又因为在上递减，‎ ‎，‎ 所以，即，‎ 故填：‎ ‎【点睛】本题主要考查函数的奇偶性和单调性的应用，考查指数函数对数函数的单调性，意在考查学生对这些知识的理解掌握水平和分析推理能力，属于较易题目。‎ ‎16.设函数的定义域为，值域为，若的最小值为，则实数的值是_____________。‎ ‎【答案】或 ‎【解析】‎ ‎【分析】‎ 根据题意，利用函数图像的变换，作出的图像，根据图像特点，结合题意，分和进行讨论，列出关于的等式关系，即可求解出结果。‎ ‎【详解】如图所示，做出的图像，‎ 若，当时，时，。‎ 若时， 当时，，。‎ 综上所述，或。‎ ‎【点睛】本题主要考查了对数函数的图像以及性质，在画对数函数图像时要注意强化讨论意识，对底数是还是进行讨。作的图像，应先作出的图像，轴上方的图像保留，轴下方的图像翻折。‎ 三、解答题（本大题共6小题，共82分．解答应写出文字说明、证明过程或演算步骤．）‎ ‎17.计算 ‎（1）；‎ ‎（2）计算：；‎ ‎（3）已知，求.‎ ‎【答案】（1）；（2）；（3）．‎ ‎【解析】‎ ‎【分析】‎ ‎（1）（2）根据分数指数幂的定义，及指数的运算性质，代入计算可得答案；‎ ‎（3）由，可得，即，将所求平方，代入即可得答案．‎ ‎【详解】（1）‎ ‎ ‎ ‎；‎ ‎（2）‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎（3）∵＝3，‎ ‎∴（）2＝x2+x﹣2+2＝9，‎ ‎∴x2+x﹣2＝7．‎ 则（）2＝x2+x﹣2﹣2＝5，‎ ‎∴．‎ ‎【点睛】此题主要考查指对幂的四则运算，熟练掌握指对幂的基本知识点很容易求解，属于简单题目。‎ ‎18.已知函数的定义域是集合,集合是实数集.‎ ‎⑴若，求；‎ ‎⑵若，求实数的取值范围.‎ ‎【答案】（1）（2）‎ ‎【解析】‎ ‎【详解】试题分析：（1）将代入求出集合P，令函数解析式有意义，求出集合，结合集合的交集，补集运算的定理，可得；‎ ‎（2）若P∪Q=Q，则P⊆Q，分P=∅和P≠∅两种情况，分别求出满足条件的实数a的取值范围，综合讨论结果，可得答案．‎ 试题解析：‎ ‎（1）‎ 当 故 ‎.‎ ‎（2）要 则要 ‎(i)当时，即时，要使得.‎ 只需 解得 ‎(ii)当 时，即时，故.‎ 综合(i)(ii)，实数 的取值范围为 ‎19.已知是关于的方程的一个实根，且是第三象限角．‎ ‎（1）求的值；‎ ‎（2）求的值．‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）形如，分子，分母同时除以，运算即可得解. ‎ ‎（2）形如，除以，构造齐次式运算即可.‎ ‎【详解】解：∵是关于的方程个实根，且是第三象限角，∴或（舍去）．‎ ‎（1）．‎ ‎（2）．‎ ‎【点睛】本题考查了同角三角函数的基本关系，中档题.‎ ‎20.某公司生产甲、乙两种产品所得利润分别为和（万元），它们与投入资金（万元）的关系有经验公式，．今将120万元资金投入生产甲、乙两种产品，并要求对甲、乙两种产品的投资金额都不低于20万元．‎ ‎（Ⅰ）设对乙产品投入资金万元，求总利润（万元）关于的函数关系式及其定义域；‎ ‎（Ⅱ）如何分配使用资金，才能使所得总利润最大？最大利润为多少？‎ ‎【答案】（Ⅰ）； （Ⅱ）当对甲产品投入资金84万元，对乙产品投入资金万元时，所得总利润最大，最大利润为71万元.‎ ‎【解析】‎ ‎【分析】‎ ‎（Ⅰ）由题得，再求函数的定义域；（Ⅱ）令，则，则原函数化为关于的函数： ‎ 再利用二次函数求最大利润.‎ ‎【详解】(Ⅰ)对乙产品投入资金万元，则对甲产品投入资万元；‎ 所以， ‎ ‎，‎ 由，解得，所以其定义域为.‎ ‎ (Ⅱ)令，则，则原函数化为关于的函数： , ‎ 所以当，即时，（万元），‎ 答：当对甲产品投入资金84万元，对乙产品投入资金万元时，所得总利润最大，最大利润为71万元.‎ ‎【点睛】本题主要考查函数解析式的求法和定义域的求法，考查函数最值的计算和函数的应用，意在考查学生对这些知识的理解掌握水平和分析推理能力.‎ ‎21.已知函数.‎ ‎(Ⅰ)证明：当变化，函数的图象恒经过定点；‎ ‎ (Ⅱ)当时，设，且，求（用表示）；‎ ‎ (Ⅲ)在(Ⅱ)的条件下，是否存在正整数，使得不等式在区间上有解，若存在，求出的最大值，若不存在，请说明理由.‎ ‎【答案】（Ⅰ）； （Ⅱ）；(Ⅲ) .‎ ‎【解析】‎ ‎【分析】‎ ‎(Ⅰ)令2x-3=1得x=2,即得定点的横坐标，代入函数解析式即得定点坐标；(Ⅱ)先求出，再利用对数的运算运算法则求；(Ⅲ)化为在区间上有解，令，求得解.‎ ‎【详解】(Ⅰ)当时，不论取何值，都有 故函数的图象恒经过定点； ‎ ‎(Ⅱ)当时，，‎ ‎，‎ ‎.‎ ‎(Ⅲ)在(Ⅱ)的条件下，不等式化为 即在区间上有解； ‎ 令，则，‎ ‎，，‎ ‎，‎ 又是正整数，故的最大值为.‎ ‎【点睛】本题主要考查对数函数的定点问题，考查对数的运算法则和对数函数的单调性，考查函数的最值的求法，意在考查学生对这些知识的理解掌握水平和分析推理能力.‎ ‎22.已知定义在区间上的函数，‎ ‎(1)判定函数在的单调性,并用定义证明；‎ ‎(2)设方程有四个不相等的实根．‎ ‎①证明：；‎ ‎②在是否存在实数，使得函数在区间单调，且的取值范围为，若存在，求出的取值范围；若不存在，请说明理由．‎ ‎【答案】(1) 在上单调递增.证明见解析； (2) ①见证明；②存在，的取值范围为 ‎【解析】‎ ‎【分析】‎ ‎(1)先判断后按照定义法证明单调性的步骤进行证明即可;‎ ‎(2) ①根据绝对值的性质，原方程可以转化为：或，利用一元二次方程根与系数的关系，可以证明出；‎ ‎②画出函数的简图，结合①可以确定的取值范围，结合图象可以确定函数的单调性，这样可以进行分类讨论，利用构造新函数、代数式的恒等变形、二次函数的单调性，结合已知函数在区间单调，且的取值范围为，最后可以求出的取值范围.‎ ‎【详解】(1)在上单调递增.‎ 证明:任取,，且.‎ ‎∵‎ 其中，，，‎ ‎∴‎ ‎∴在上单调递增. ‎ ‎(2)①或 即或 ‎∵为方程的四个不相等的实根 ‎∴由根与系数的关系得 ‎②如图，‎ 可知，在区间、上均为单调函数 ‎(i)当时，在上单调递增 则,即,在有两个不等实根 而令,则 由二次函数的单调性，可得， ‎ ‎(ii)当时，在上单调递减 则两式相除整理得 ‎∴,∴,∴‎ 由,得 ‎∴ ‎ 综上，的取值范围为 ‎【点睛】本题考查了用定义证明函数的单调性，考查了方程根之间的关系的证明，考查了二次函数的单调性，考查了构造函数法，考查了函数图象的应用.‎ ‎ ‎