高中数学选修2-3课件2_3_2《期望在生活中的应用》 18页

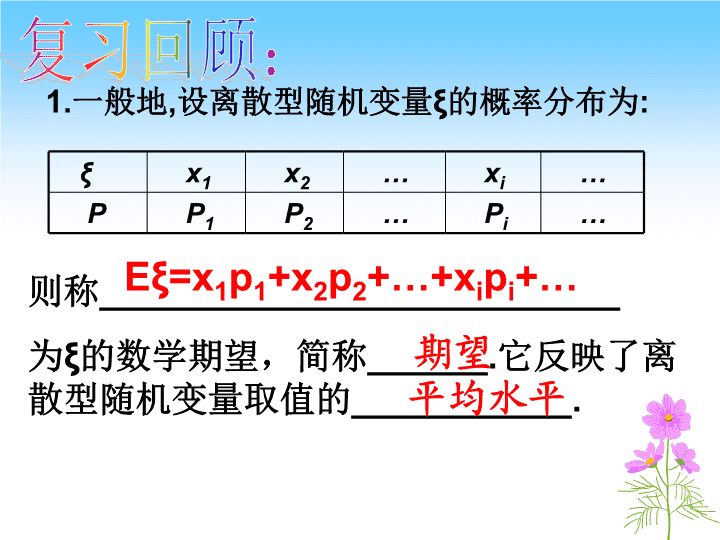
期望在生活中的应用 人人学有价值的数学 Eξ=x 1 p 1 +x 2 p 2 +…+x i p i +… 1. 一般地 , 设离散型随机变量 ξ 的概率分布为 : ξ x 1 x 2 … x i … P P 1 P 2 … P i … 则称 __________________________ 为 ξ 的数学期望， 简称 ______. 它反映了离散型随机变量取值的 ___________. 平均水平 期望 复习回顾： 1 . 若 ξ 是随机变量 ,η=aξ+b, 则 E(aξ+b)=________. 2. 若 ξ~B(n,p), 则 Eξ=____. 3. 若随机变量 ξ 服从几何分布 , 且 P(ξ=k)=g(k,p), 则 Eξ=____. aEξ+b np p 1 ２ . 期望的性质 : 姚明的投篮命中率为 0.8 ，假设他每次命中率相同 , 他在某次训练中连续投篮， 直到 进球为止，则他的平均投篮次数 是多少 ? 一 . 投篮次数问题 （ 2006. 湖南 ) 某安全生产监督部门对 5 家小型煤矿进行安全检查 ( 简称安检 ). 若安检不合格 , 则必须整改 . 若整改后经复查仍不合格 , 则强行关闭 . 设每家煤矿安检是否合格是相互独立的 , 且每家煤矿整改前安检合格的概率是 0.5. 则 平均有多少家煤矿必须整改 ? 解 : 由题设 , 必须整改的煤矿数 从而 的数学期望是 答 : 平均有 2.5 家煤矿必须整改 . 二 . 安全生产问题 例 . 目前由于各种原因 , 许多人选择租车代步 , 租车行业生意十分兴隆 , 但由于租车者以新手居多 , 车辆受损事故频频发生 . 据统计 , 一年中一辆车受损的概率为 0.03 . 现保险公司拟开设一年期租车保险 , 一辆车一年的保险费为 1000 元 , 若在一年内该车受损 , 则保险公司需赔偿 3000 元 , 求保险公司收益的期望 . 两点分布 三 . 保险公司收益问题 0.03 0.97 P -2000 1000 一年内保险公司收益 的分布列： 假如你 是一位商场经理 , 在 十一那天想举行促销活动 , 根据统计资料显示 : (1). 若在商场内举行促销活动 , 可获利 2 万元 (2). 若在商场外举行促销活动 , 则要看天气情况 : 不下雨可获利 10 万元 , 下雨则要损失 4 万元 . 气象台预报十一那天有雨的概率是 40%, 你应选择哪种促销方式？ 四 . 商场促销问题 商场促销问题 解：设商场在商场外的促销活动中获得经济效益为 万元 , 则 的分布列为： 0.4 0.6 P － 4 10 E = 10×0.6 ＋ ( － 4) ×0.4 = 4.4 万元 变式 1 ： 若下雨的概率为 0.6 呢 ? 变式 2: 下雨的概率为多少时 , 在商场内、外搞 促销没有区别 . ＞ 2 万元 , 故应选择在商场外搞促销活动 . B 队队员胜的概率 现按表中对阵方式出场，每场胜队得 1 分，负队得 0 分 . 设 A 队最后所得总分为 , 求 A 队最后所得总分的期望 . 五 . 比赛得分问题 六 . 摸彩中奖问题 一个布袋内装有 6 个红球与 6 个黄球，除颜色不同外，六个球完全一样，每次从袋中摸 6 个球，输赢的规则为： 6 个全红 赢得 100 元 5 红 1 黄 赢得 50 元 4 红 2 黄 赢得 20 元 3 红 3 黄 输 100 元 2 红 4 黄 赢得 20 元 1 红 5 黄 赢得 50 元 6 个全黄 赢得 100 元 其中只有一种情况输，而对于其它六种情况 你均能赢得相应的钱数，而不用花其它的钱。 摸奖人赢钱的期望有多大？ 设 ξ 为赢得的钱数 , 则 ξ 的分布列如下 : 所以每摸一次，平均输掉 29.34 元 解 : ξ 100 50 20 -100 p 说明 : 事实上 , 任何赌博、彩票都是不公平的 , 否则赌场的巨额开销和业主的高额利润从何而来 ? 在我国 , 彩票发行只有当收益主要用于公益事业时才允许 . 概率 核心 , 难点 分清问题实质，解决问题 ! 二项分布 分布列 　几何分布 期望 应用 思考题 北 京 广 州 3 2 2 1 4 1 如图 , 广州到北京之间有 6 条不同的网络线路并联 , 它们能通过的最大信息量分别为 1 、 1 、 2 、 2 、 3 、 4. 现从中任取三条网线且使每条网线通过最大信息量 , 三条网线可通过的信息总量即为三条网线各自的最大信息量之和 . (1) 求选取的三条网线可通过信息 总量 ξ 的数学期望 ; (2) 当 ξ≥6 时 , 则保证信息畅通 , 求线路信息畅 通的概率 ; (3) 2008 年北京奥运会 , 为保证广州网络在 ξ≥6 时信息畅通的概 率超过 85%, 需要增加一条网线且最大信息量不低于 3, 问增加 的这条网线的最大信息量最少应为多少 ? ξ 4 5 6 7 8 9 P 解 : ξ 的分布列为 (3) 2008 年北京奥运会 , 为保证广州网络在 ξ≥6 时信息畅通的概率超过 85%, 需要增加一条网线且最大信息量不低于 3, 问增加的这条网线的最大信息量最少应为多少 ? 北 京 广州 3 2 2 1 4 1