2012高中数学人教A版必修3综合测试题及答案 1 10页

必修3综合模块测试（人教A版必修3）‎ 一、选择题：‎ 1. 高二年级有14个班，每个班的同学从1到50排学号，为了交流学习经验，要求每班学号为14的同学留下来进行交流，这里运用的是（ ）‎ ‎ A．分层抽样 B．抽签抽样 C．随机抽样 D．系统抽样 ‎ 2. 五进制数转化为八进制数是（ ）‎ A. B. C. D.‎ 3. 计算机执行下面的程序，输出的结果是( )‎ a=1 ‎ b=3 ‎ a=a+b ‎ b=ba ‎ PRINT a，b END A、1，3 B、4，‎9 C、4，12 D、4，8 ‎ 4. 甲,乙两人随意入住两间空房,则甲乙两人各住一间房的概率是 ( )‎ A.　 　 B.　　 　 C. 　　 D.无法确定 5. 如下四个游戏盘,现在投镖,投中阴影部分概率最大的是 ( )‎ 开始 i=1‎ s=0‎ i=i+1‎ s=s+i i≤5?‎ 输出s 结束 ①‎ ②‎ a ‎ 是 ‎ 否 6. 下图是2013年我校举办“激扬青春,勇担责任”演讲比赛大赛上,‎ 七位评委为某位选手打出的分数的茎叶图,去掉一个最高分和一 个最低分后,所剩数据的中位数和平均数分别为 ( ) ‎ ‎7 9‎ ‎8 4 4 4 6 7‎ ‎9 3 ‎ A.85;87 B.84; ‎86 ‎‎ ‎C.84;85 D.85;86 ‎ 7. 如右图的程序框图(未完成).设当箭头a指向①时,输出的结果 s=m,当箭头a指向②时,输出的结果s=n,则m+n= ( )‎ A.30 B‎.20 ‎‎ C.15 D.5‎ 8. ‎10个正数的平方和是370，方差是33，那么平均数为（ ）‎ A．1　　 　B．‎2　‎ 　C．3　　 　D．4‎ 1. 读程序　　　　　　　　　　　　　　　　　　　　　‎ 甲：INPUT i＝1 乙：INPUT i＝1000‎ ‎ S＝0 S＝0‎ ‎ WHILE i＜＝1000 DO ‎ S＝S＋i S＝S＋i ‎ i＝i＋l i＝i一1‎ ‎ WEND LOOP UNTIL i＜1‎ ‎ PRINT S PRINT S END END 对甲乙两程序和输出结果判断正确的是（ ）‎ A．程序不同，结果不同 B．程序不同，结果相同　‎ C．程序相同，结果不同 D．程序相同，结果相同 2. 已知点P是边长为4的正方形内任一点，则P到四个顶点的距离均大于2的概率是（ ）‎ ‎ A. B. C. D. ‎ 3. 甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为,再由乙猜甲刚才所想的数字,把乙猜的数字记为,其中,若,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( ) A. B. C. D.‎ 4. 如右的程序框图可用来估计圆周率的值.设是产生随机数的函数,它能随机产生区间内的任何一个数,如果输入1000,输出的结果为786,则运用此方法,计算的近似值为 ( )‎ A.3.144 B.‎3.141 C.3.142 D.3.143‎ 二、填空题：‎ 5. 语句“PRINT 37 MOD ‎5 ”‎运行的结果是＿＿＿＿.‎ 6. 阅读右边的流程图，‎ 若则输出的数是_＿___；‎ 7. ‎5280和2155的最大公约数是＿＿＿＿.‎ 8. 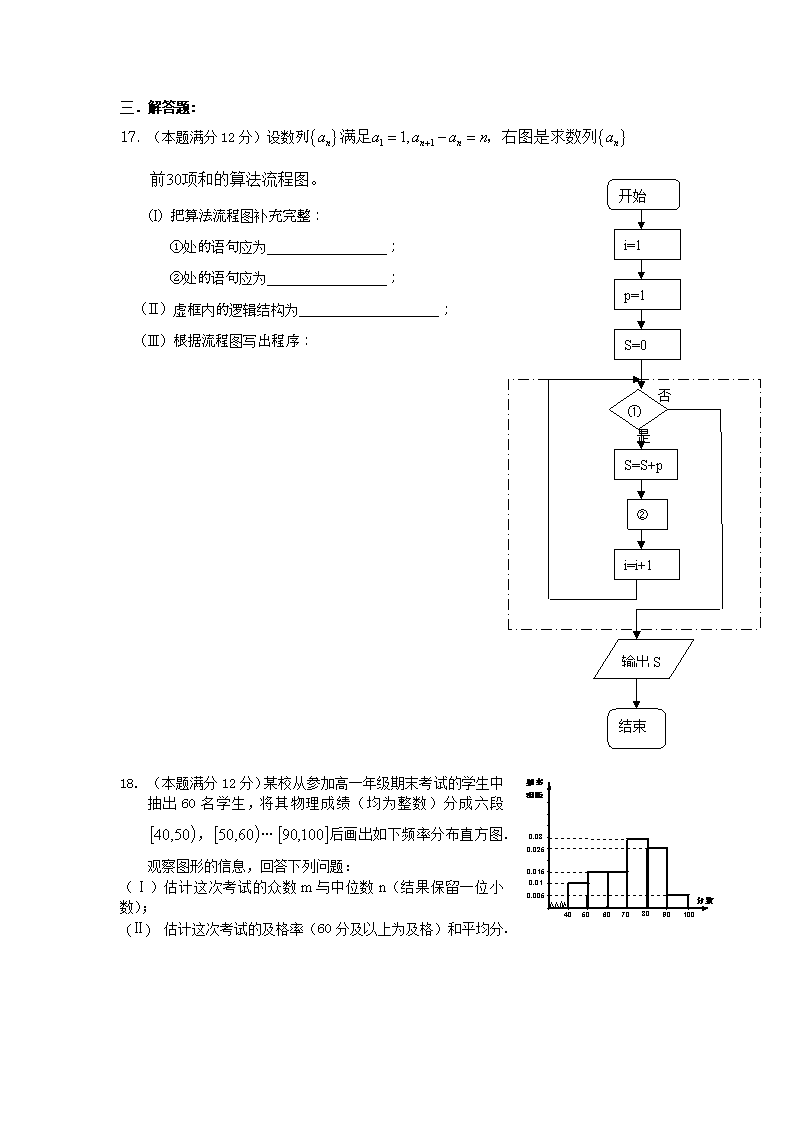乙两艘轮船都要停靠同一个泊位，它们可以在一昼夜（零点至24点）的任意时刻到达，设甲、乙两艘轮船停靠泊位的时间分别是3小时和5小时，则有一艘轮船停靠泊位时必须等待一段时间的概率为＿＿＿＿（用分数表示）．‎ 三．解答题: ‎ 1. ‎（本题满分12分）设数列 i=1‎ p=1‎ S=0‎ ‎ 否 ‎ 是 ‎①‎ S=S+p ‎②‎ i=i+1‎ 结束 开始 输出S ‎。‎ ‎(I) 把算法流程图补充完整：‎ ‎①处的语句应为 ；‎ ‎②处的语句应为 ；‎ ‎(Ⅱ) 虚框内的逻辑结构为 ；‎ ‎(Ⅲ) 根据流程图写出程序：‎ ‎ ‎ ‎ ‎ 2. ‎（本题满分12分）某校从参加高一年级期末考试的学生中抽出60名学生，将其物理成绩（均为整数）分成六段，…后画出如下频率分布直方图.观察图形的信息，回答下列问题：‎ ‎（Ⅰ）估计这次考试的众数m与中位数n（结果保留一位小数）；‎ ‎(Ⅱ) 估计这次考试的及格率（60分及以上为及格）和平均分.‎ 1. ‎（本题满分12分）假设关于某设备的使用年限和所支出的维修费用(万元),有如下的统计数据由资料知对呈线性相关,并且统计的五组数据得平均值分别为,,若用五组数据得到的线性回归方程去估计,使用8年的维修费用比使用7年的维修费用多1.1万元,‎ ‎（1）求回归直线方程;‎ ‎（2）估计使用年限为10年时,维修费用是多少?‎ 2. ‎（本题满分12分）设函数，若a是从1，2，3三个数中任取一个数，b是从2，3，4，5四个数中任取一个数，⑴求的最小值；⑵求恒成立的概率.‎ 3. ‎（本题满分13分）在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球，现从甲、乙两个盒子中各取出1个球，每个球被取出的可能性相等．‎ ‎（Ⅰ）求取出的两个球上标号为相同数字的概率；‎ ‎（Ⅱ）求取出的两个球上标号之积能被3整除的概率．‎ 1. ‎（本题满分13分）请认真阅读下列程序框图：‎ ‎ 已知程序框图中的函数关系式为，程序框图中的D为函数的定义域，把此程序框图中所输出的数组成一个数列.‎ ‎⑴若输入，请写出数列的所有项； ‎ ‎⑵若输出的无穷数列是一个常数列，试求输入的初始值的值； ‎ ‎ ⑶若输入一个正数时，产生的数列满足：任意一项，都有，试求 正数的取值范围. ‎ 开始 输出xi 结束 i＝1‎ i＝i＋1‎ 是 否 输入x0‎ 是 否 参考答案 一.选择题（60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A D C C A C B B B A D A 二．填空题（16分）‎ ‎13、 2 . 14、 .‎ i=1‎ p=1‎ S=0‎ ‎ 否 ‎ 是 ‎①‎ S=S+p ‎②‎ i=i+1‎ 结束 开始 输出S ‎15、 5 . 16、 . ‎ ‎17.解 (Ⅰ)① i≤30 ② p=p+i ‎ ‎(Ⅱ)当型循环结构 ‎ ‎(Ⅲ) ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎18.解：（Ⅰ）众数是最高小矩形中点的横坐标，所以众数为m＝75分；‎ ‎ 前三个小矩形面积为，‎ ‎∵中位数要平分直方图的面积，∴‎ ‎（Ⅱ）依题意，60及以上的分数所在的第三、四、五、六组，‎ 频率和为 ‎ 所以，抽样学生成绩的合格率是% ‎ 利用组中值估算抽样学生的平均分 ‎ ‎ ‎＝‎ ‎＝71‎ 估计这次考试的平均分是71分 ‎19.解：(1)因为线性回归方程经过定点,将,代入回归方程得; 又;解得, 线性回归方程 ………………6分 ‎(2)将代入线性回归方程得(万元)‎ ‎ ∴线性回归方程;使用年限为10年时,维修费用是21(万元).……………12分 ‎20.解：⑴‎ ‎…………………………2分 ‎……………4分 ‎……………………6分 ‎⑵恒成立就转化为成立.‎ 设事件A：“恒成立”，则 基本事件总数为12个，即 ‎（1，2），（1，3），（1，4），（1，5）；‎ ‎（2，2），（2，3），（2，4），（2，5）；‎ ‎（3，2），（3，3），（3，4），（3，5）；…………………………8分 事件A包含事件：（1，2），（1，3）；‎ ‎（2，2），（2，3），（2，4），（2，5）；‎ ‎（3，2），（3，3），（3，4），（3，5）共10个……………………10分 由古典概型得……………………12分 备注：利用加法、乘法原理同样给分.‎ ‎21.解：设从甲、乙两个盒子中各取1个球，其数字分别为，‎ 用表示抽取结果，则所有可能的结果有16种，即 ‎，，，，，，，，‎ ‎，，，，，，，． ‎ ‎（Ⅰ）设“取出的两个球上的标号相同”为事件A，‎ 则． ‎ 事件A由4个基本事件组成，故所求概率． ‎ 答：取出的两个球上的标号为相同数字的概率为． ‎ ‎（Ⅱ）设“取出的两个球上标号的数字之积能被3整除”为事件B，‎ 则． ‎ 事件B由7个基本事件组成，故所求概率．‎ 答：取出的两个球上标号之积能被3整除的概率为． ‎ ‎22. 解：（1）当时，‎ ‎ 所以输出的数列为 ‎ （2）数列是一个常数列，则有 ‎ 即 ，解得：‎ ‎ 所以输入的初始值为1或2时输出的为常数列.‎ ‎ (3)由题意知 ，因，‎ ‎ ，有： 得 ‎ 即，即 ‎ 要使任意一项，都有，须，解得：，‎ ‎ 所以当正数在(1，2)内取值时，所输出的数列对任意正整数n满足。‎ ‎ ‎