高一数学（人教A版）必修4能力提升：1-4-2-2 正、余弦函数的性质 7页

能 力 提 升 一、选择题 ‎1．y＝2sinx2的值域是(　　)‎ A．[－2,2] B．[0,2]‎ C．[－2,0] D．R ‎[答案]　A ‎[解析]　∵x2≥0，∴sinx2∈[－1,1]，‎ ‎∴y＝2sinx2∈[－2,2]．‎ ‎2．函数y＝是(　　)‎ A．奇函数 B．偶函数 C．既是奇函数又是偶函数 D．既不是奇函数也不是偶函数 ‎[答案]　A ‎[解析]　定义域为R，f(－x)＝＝＝－f(x)，则f(x)是奇函数．‎ ‎3．已知a∈R，函数f(x)＝sinx－|a|，x∈R为奇函数，则a等于(　　)‎ A．0　　　　B．‎1　‎　　　C．－1　　　D．±1‎ ‎[答案]　A ‎[解析]　解法一：易知y＝sinx在R上为奇函数，‎ ‎∴f(0)＝0，∴a＝0.‎ 解法二：∵f(x)为奇函数，∴f(－x)＝－f(x)，即sin(－x)－|a|＝－sinx＋|a|，－sinx－|a|＝－sinx＋|a|.‎ ‎∴|a|＝0，即a＝0.‎ ‎4．(重庆高考)下列函数中，周期为π，且在[，]上为减函数的是(　　)‎ A．y＝sin(2x＋) B．y＝cos(2x＋)‎ C．y＝sin(x＋) D．y＝cos(x＋)‎ ‎[答案]　A ‎[解析]　C、D两项中函数的周期都为2π，不合题意，排除C、D；B项中y＝cos(2x＋)＝－sin2x，该函数在[，]上为增函数，不合题意；A项中y＝sin(2x＋)＝cos2x，该函数符合题意，选A.‎ ‎5．(陕西高考)对于函数f(x)＝sin2x，下列选项中正确的是(　　)‎ A．f(x)在(，)上是递增的 B．f(x)的图象关于原点对称 C．f(x)的最小正周期为2π D．f(x)的最大值为2‎ ‎[答案]　B ‎[解析]　由于函数y＝sinx在(，π)上是递减的，所以f(x)＝sin2x在(，)上是递减的，故A选项错误．‎ 因为f(－x)＝sin2(－x)＝sin(－2x)＝－sin2x＝－f(x)，所以f(x)为奇函数，图象关于原点对称，故B选项正确．‎ ‎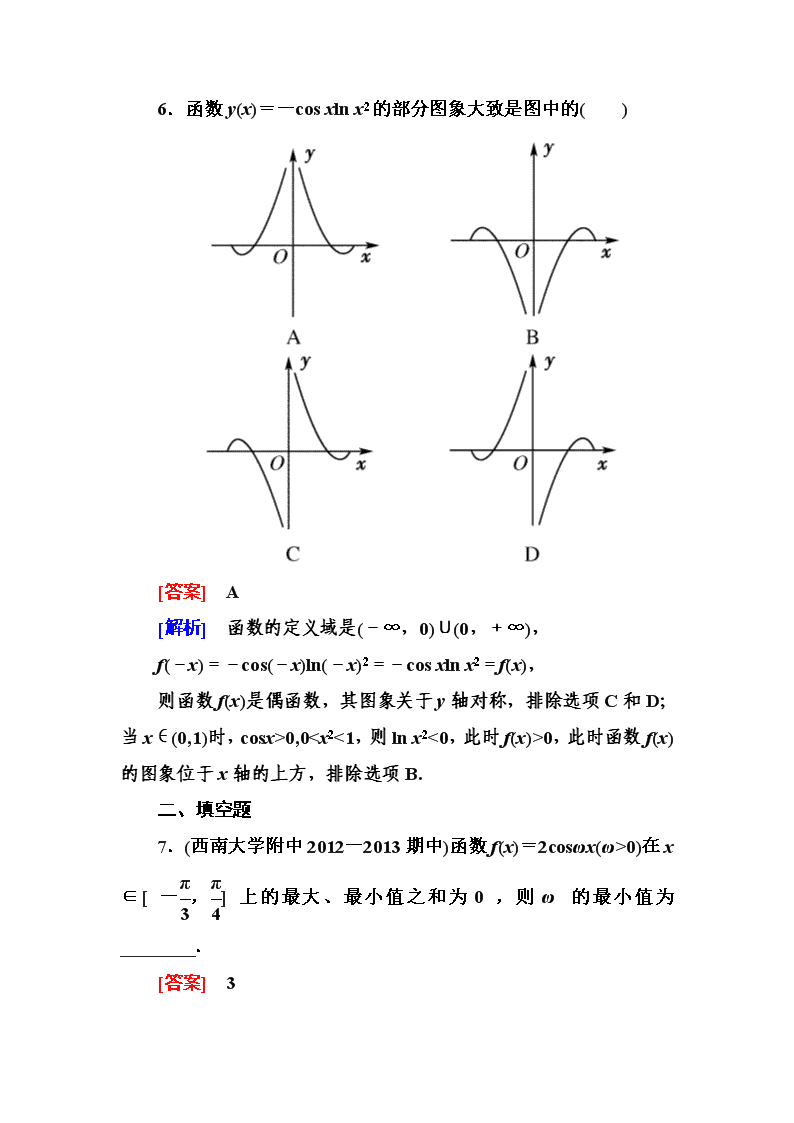6．函数y(x)＝－cos xln x2的部分图象大致是图中的(　　)‎ ‎[答案]　A ‎[解析]　函数的定义域是(－∞，0)∪(0，＋∞)，‎ f(－x)＝－cos(－x)ln(－x)2＝－cos xln x2＝f(x)，‎ 则函数f(x)是偶函数，其图象关于y轴对称，排除选项C和D；当x∈(0,1)时，cosx>0,00，此时函数f(x)的图象位于x轴的上方，排除选项B.‎ 二、填空题 ‎7．(西南大学附中2012－2013期中)函数f(x)＝2cosωx(ω>0)在x∈[－，]上的最大、最小值之和为0，则ω的最小值为________．‎ ‎[答案]　3‎ ‎8．(2012·长沙调研)已知函数f(x)＝3sin(ωx－)(ω>0)和g(x ‎)＝2cos(2x＋φ)＋1的图象的对称轴完全相同，若x∈[0，]，则f(x)的取值范围是____________．‎ ‎[答案]　[－，3]‎ ‎[解析]　∵f(x)与g(x)的图象的对称轴完全相同，‎ ‎∴f(x)与g(x)的最小正周期相等，‎ ‎∵ω>0，∴ω＝2，∴f(x)＝3sin(2x－)，‎ ‎∵0≤x≤，∴－≤2x－≤，‎ ‎∴－≤sin(2x－)≤1，‎ ‎∴－≤3sin(2x－)≤3，‎ 即f(x)的取值范围是[－，3]．‎ ‎9．(2011～2012·无锡高一检测)函数y＝sin(x－)，x∈[0，π]的值域为________．‎ ‎[答案]　[－，1]‎ 三、解答题 ‎10．求函数y＝cos＋1的最大值，及此时自变量x的取值集合．‎ ‎[解析]　∵x∈R，∴－1≤cos≤1.‎ ‎∴≤cos＋1≤.‎ ‎∴函数y＝cos＋1的最大值是.‎ 此时2x－＝2kπ(k∈Z)，∴x＝kπ＋.‎ 即此时自变量x的取值集合是 .‎ ‎11．已知函数f(x)＝log|sinx|.‎ ‎(1)求其定义域和值域；‎ ‎(2)判断其奇偶性；‎ ‎(3)求其周期；‎ ‎(4)写出单调区间．‎ ‎[解析]　(1)由|sinx|>0得sinx≠0，∴x≠kπ(k∈Z)．‎ 即函数定义域为{x∈R|x≠kπ，k∈Z}．‎ 又0<|sinx|≤1，∴log|sinx|≥0.‎ ‎∴函数的值域为[0，＋∞)．‎ ‎(2)∵f(x)的定义域关于原点对称，‎ 且f(－x)＝log|sin(－x)|＝log|－sinx|‎ ‎＝log|sinx|＝f(x)．‎ ‎∴f(x)为偶函数．‎ ‎(3)函数f(x)是周期函数，‎ ‎∵f(x＋π)＝log|sin(x＋π)|＝log|－sinx|‎ ‎＝log|sinx|＝f(x)，‎ ‎∴f(x)的周期T＝π.‎ ‎(4)∵y＝logu在(0，＋∞)上是减函数，‎ u＝|sinx|在(k∈Z)上是增函数，‎ 在(k∈Z)上是减函数．‎ ‎∴f(x)在(k∈Z)上是增函数，‎ 在(k∈Z)上是减函数．‎ 即f(x)的单调增区间是(k∈Z)，‎ 单调减区间是(k∈Z)．‎ ‎12．设函数f(x)＝sin2x＋acosx＋a－，x∈[0，]的最大值是1，试确定a的值．‎ ‎[解析]　f(x)＝sin2x＋acosx＋a－＝1－cos2x＋acosx＋a－＝－(cosx－)2＋(‎2a2＋‎5a－4)．(1)若0≤≤1，即0≤a≤2，当cosx＝时，‎ f(x)最大，此时(‎2a2＋‎5a－4)＝1，解得a＝；‎ ‎(2)若>1，即a>2，当x＝0时，即cosx＝1时，‎ f(x)最大，此时－(1－)2＋(‎2a2＋‎5a－4)＝1，‎ 解得a＝(不符合条件，舍去)；‎ ‎(3)若<0，即a<0，当x＝时，即cosx＝0时，‎ f(x)最大，此时－(0－)2＋(‎2a2＋‎5a－4)＝1，‎ 解得a＝(不符合条件，舍去)．综上可得a＝.‎