- 549.17 KB
- 2021-06-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
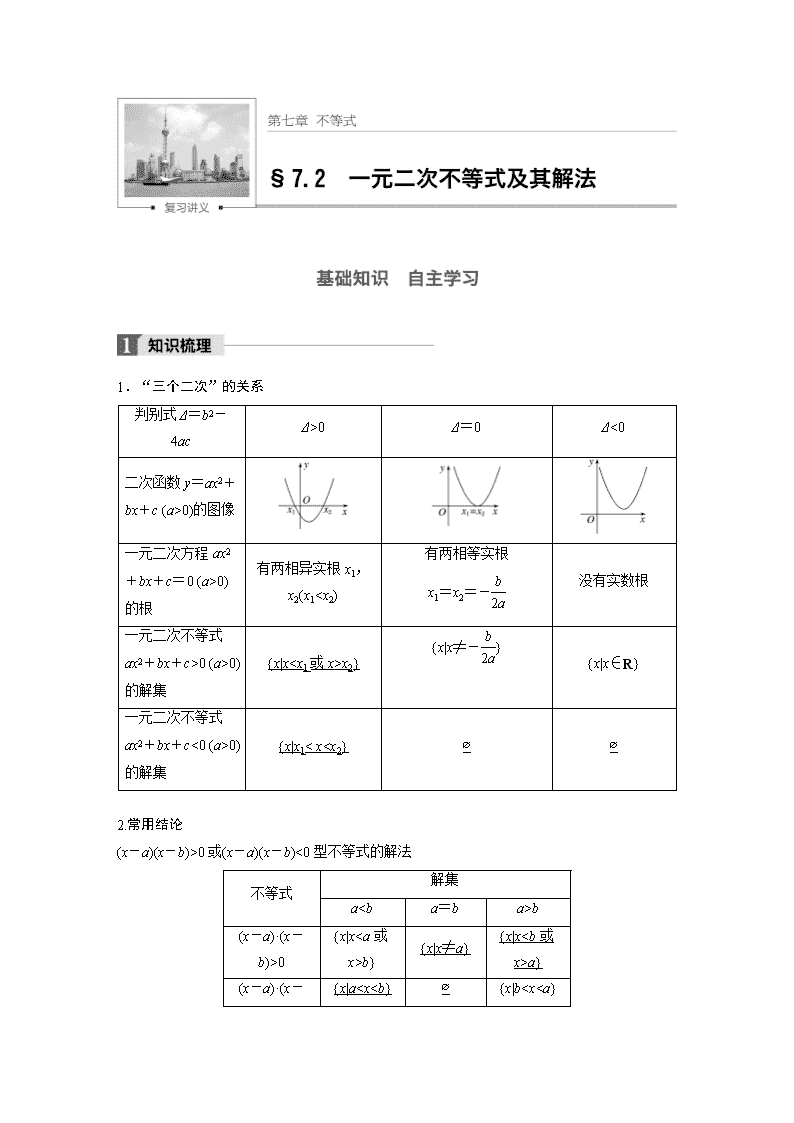
1.“三个二次”的关系
判别式Δ=b2-4ac
Δ>0
Δ=0
Δ<0
二次函数y=ax2+bx+c (a>0)的图像
一元二次方程ax2+bx+c=0 (a>0)的根
有两相异实根x1,x2(x10 (a>0)的解集
{x|xx2}
{x|x≠-}
{x|x∈R}
一元二次不等式ax2+bx+c<0 (a>0)的解集
{x|x1< x0或(x-a)(x-b)<0型不等式的解法
不等式
解集
ab
(x-a)·(x-b)>0
{x|xb}
{x|x≠a}
{x|xa}
(x-a)·(x-
{x|a0(<0)⇔f(x)·g(x)>0(<0).
(2)≥0(≤0)⇔f(x)·g(x)≥0(≤0)且g(x)≠0.
以上两式的核心要义是将分式不等式转化为整式不等式.
【思考辨析】
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)若不等式ax2+bx+c<0的解集为(x1,x2),则必有a>0.( √ )
(2)若不等式ax2+bx+c>0的解集是(-∞,x1)∪(x2,+∞),则方程ax2+bx+c=0的两个根是x1和x2.( √ )
(3)若方程ax2+bx+c=0(a≠0)没有实数根,则不等式ax2+bx+c>0的解集为R.( × )
(4)不等式ax2+bx+c≤0在R上恒成立的条件是a<0且Δ=b2-4ac≤0.( × )
(5)若二次函数y=ax2+bx+c的图像开口向下,则不等式ax2+bx+c<0的解集一定不是空集.( √ )
1.(教材改编)不等式x2-3x-10>0的解集是( )
A.(-2,5) B.(5,+∞)
C.(-∞,-2) D.(-∞,-2)∪(5,+∞)
答案 D
解析 解方程x2-3x-10=0得x1=-2,x2=5,
由于y=x2-3x-10的图像开口向上,所以x2-3x-10>0的解集为(-∞,-2)∪(5,+∞).
2.设集合M={x|x2-3x-4<0},N={x|0≤x≤5},则M∩N等于( )
A.(0,4] B.[0,4)
C.[-1,0) D.(-1,0]
答案 B
解析 ∵M={x|x2-3x-4<0}={x|-10,
令3x2-2x-2=0,得x1=,x2=,
∴3x2-2x-2>0的解集为(-∞,)∪(,+∞),即函数y=log2(3x2-2x-2)的定义域是(-∞,)∪(,+∞).
4.(教材改编)若关于x的不等式ax2+bx+2>0的解集是(-,),则a+b=________.
答案 -14
解析 ∵x1=-,x2=是方程ax2+bx+2=0的两个根,∴解得∴a+b=-14.
5.不等式x2+ax+4≤0的解集不是空集,则实数a的取值范围是________________.
答案 (-∞,-4]∪[4,+∞)
解析 ∵x2+ax+4≤0的解集不是空集,
∴x2+ax+4=0一定有解.
∴Δ=a2-4×1×4≥0,即a2≥16,∴a≥4或a≤-4.
题型一 一元二次不等式的求解
命题点1 不含参数的不等式
例1 求不等式-2x2+x+3<0的解集.
解 化-2x2+x+3<0为2x2-x-3>0,
解方程2x2-x-3=0,得x1=-1,x2=,
∴不等式2x2-x-3>0的解集为(-∞,-1)∪(,+∞),即原不等式的解集为(-∞,-1)∪(,+∞).
命题点2 含参数的不等式
例2 解关于x的不等式:x2-(a+1)x+a<0.
解 由x2-(a+1)x+a=0,得(x-a)(x-1)=0,
∴x1=a,x2=1,
①当a>1时,x2-(a+1)x+a<0的解集为{x|11.
若a<0,原不等式等价于(x-)(x-1)>0,
解得x<或x>1.
若a>0,原不等式等价于(x-)(x-1)<0.
①当a=1时,=1,(x-)(x-1)<0无解;
②当a>1时,<1,解(x-)(x-1)<0,
得1,解(x-)(x-1)<0,
得11};
当a=0时,解集为{x|x>1};
当01时,解集为{x|0,则a的取值范围是( )
A.(0,4) B.[0,4)
C.(0,+∞) D.(-∞,4)
答案 (1)D (2)B
解析 (1)∵2kx2+kx-<0为一元二次不等式,
∴k≠0,
又2kx2+kx-<0对一切实数x都成立,
则必有解得-30,则必有或a=0,∴0≤a<4.
命题点2 在给定区间上的恒成立问题
例4 设函数f(x)=mx2-mx-1.若对于x∈[1,3],f(x)<-m+5恒成立,求m的取值范围.
解 要使f(x)<-m+5在x∈[1,3]上恒成立,
即m2+m-6<0在x∈[1,3]上恒成立.
有以下两种方法:
方法一 令g(x)=m2+m-6,x∈[1,3].
当m>0时,g(x)在[1,3]上是增加的,
所以g(x)max=g(3)⇒7m-6<0,
所以m<,所以00,
又因为m(x2-x+1)-6<0,所以m<.
因为函数y==在[1,3]上的最小值为,所以只需m<即可.
所以,m的取值范围是.
命题点3 给定参数范围的恒成立问题
例5 对任意m∈[-1,1],函数f(x)=x2+(m-4)x+4-2m的值恒大于零,求x的取值范围.
解 由f(x)=x2+(m-4)x+4-2m
=(x-2)m+x2-4x+4,
令g(m)=(x-2)m+x2-4x+4.
由题意知在[-1,1]上,g(m)的值恒大于零,
∴
解得x<1或x>3.
故当x的取值范围为(-∞,1)∪(3,+∞)时,对任意的m∈[-1,1],函数f(x)
的值恒大于零.
思维升华 (1)对于一元二次不等式恒成立问题,恒大于0就是相应的二次函数的图像在给定的区间上全部在x轴上方,恒小于0就是相应的二次函数的图像在给定的区间上全部在x轴下方.另外常转化为求二次函数的最值或用分离参数法求最值.
(2)解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.
(1)已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是________.
答案 (-,0)
解析 作出二次函数f(x)的草图,
对于任意x∈[m,m+1],都有f(x)<0,
则有
即解得-,不满足题意;
当m≠0时,函数f(x)=mx2-2x-m+1为二次函数,
需满足开口向下且方程mx2-2x-m+1=0无解,即
不等式组的解集为空集,
即m无解.
综上可知,不存在这样的m.
题型三 一元二次不等式的应用
例6 某商品每件成本价为80元,售价为100元,每天售出100件.若售价降低x成(1成=10%),售出商品数量就增加x成.要求售价不能低于成本价.
(1)设该商店一天的营业额为y,试求y与x之间的函数关系式y=f(x),并写出定义域;
(2)若再要求该商品一天营业额至少为10 260元,求x的取值范围.
解 (1)由题意得,y=100·100.
因为售价不能低于成本价,所以100-80≥0.
所以y=f(x)=40(10-x)(25+4x),定义域为x∈[0,2].
(2)由题意得40(10-x)(25+4x)≥10 260,
化简得8x2-30x+13≤0,解得≤x≤.
所以x的取值范围是.
思维升华 求解不等式应用题的四个步骤
(1)阅读理解,认真审题,把握问题中的关键量,找准不等关系.
(2)引进数学符号,将文字信息转化为符号语言,用不等式表示不等关系,建立相应的数学模型.
(3)解不等式,得出数学结论,要注意数学模型中自变量的实际意义.
(4)回归实际问题,将数学结论还原为实际问题的结果.
甲厂以x千克/小时的速度匀速生产某种产品(生产条件要求1≤x≤10),每小时可获得的利润是100·(5x+1-)元.
(1)要使生产该产品2小时获得的利润不低于3 000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润.
解 (1)根据题意,得200(5x+1-)≥3 000,
整理得5x-14-≥0,即5x2-14x-3≥0,
又1≤x≤10,可解得3≤x≤10.
即要使生产该产品2小时获得的利润不低于3 000元,x的取值范围是[3,10].
(2)设利润为y元,则
y=·100(5x+1-)
=9×104(5+-)
=9×104[-3(-)2+],
故当x=6时,ymax=457 500元.
即甲厂以6千克/小时的生产速度生产900千克该产品时获得的利润最大,最大利润为457 500元.
思维升华 求解不等式应用题的四个步骤
(1)阅读理解,认真审题,把握问题中的关键量,找准不等关系.
(2)引进数学符号,将文字信息转化为符号语言,用不等式表示不等关系,建立相应的数学模型.
(3)解不等式,得出数学结论,要注意数学模型中自变量的实际意义.
(4)回归实际问题,将数学结论还原为实际问题的结果.
14.转化与化归思想在不等式中的应用
典例 (1)已知函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞),若关于x的不等式f(x)0恒成立,则实数a的取值范围是________.
思想方法指导 函数的值域和不等式的解集转化为a,b满足的条件;不等式恒成立可以分离常数,转化为函数值域问题.
解析 (1)由题意知f(x)=x2+ax+b
=2+b-.
∵f(x)的值域为[0,+∞),
∴b-=0,即b=.
∴f(x)=2.
又∵f(x)0恒成立,
即x2+2x+a>0恒成立.
即当x≥1时,a>-(x2+2x)=g(x)恒成立.
而g(x)=-(x2+2x)=-(x+1)2+1在[1,+∞)上是减少的,
∴g(x)max=g(1)=-3,故a>-3.
∴实数a的取值范围是{a|a>-3}.
答案 (1)9 (2){a|a>-3}
1.不等式(x-1)(2-x)≥0的解集为( )
A.{x|1≤x≤2} B.{x|x≤1或x≥2}
C.{x|12}
答案 A
解析 由(x-1)(2-x)≥0可知(x-2)(x-1)≤0,
所以不等式的解集为{x|1≤x≤2}.
2.(2016·潍坊模拟)函数f(x)=的定义域是( )
A.(-∞,1)∪(3,+∞) B.(1,3)
C.(-∞,2)∪(2,+∞) D.(1,2)∪(2,3)
答案 D
解析 由题意得-x2+4x-3>0,即x2-4x+3<0,
∴1f(1)的解集是( )
A.(-3,1)∪(3,+∞)
B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞)
D.(-∞,-3)∪(1,3)
答案 A
解析 由题意得或
解得-33.
5.已知不等式x2-2x-3<0的解集为A,不等式x2+x-6<0的解集为B,不等式x2+ax+b<0的解集为A∩B,那么a+b等于( )
A.-3 B.1
C.-1 D.3
答案 A
解析 由题意,A={x|-10)的解集为(x1,x2),且x2-x1=15,则a等于( )
A. B.
C. D.
答案 A
解析 由x2-2ax-8a2<0,
得(x+2a)(x-4a)<0,因为a>0,
所以不等式的解集为(-2a,4a),
即x2=4a,x1=-2a,由x2-x1=15,
得4a-(-2a)=15,解得a=.
7.已知不等式ax2-bx-1≥0的解集是,则不等式x2-bx-a<0的解集是( )
A.(2,3) B.(-∞,2)∪(3,+∞)
C. D.∪
答案 A
解析 由题意知-,-是方程ax2-bx-1=0的根,所以由根与系数的关系得-+=,-×=-.解得a=-6,b=5,不等式x2-bx-a<0,
即x2-5x+6<0,解集为(2,3).
8.已知函数f(x)=-x2+ax+b2-b+1(a∈R,b∈R),对任意实数x都有f(1-x)=f(1+x)成立,当x∈[-1,1]时,f(x)>0恒成立,则b的取值范围是( )
A.-12
C.b<-1或b>2 D.不能确定
答案 C
解析 由f(1-x)=f(1+x)知f(x)图像的对称轴为直线x=1,
则有=1,故a=2.
由f(x)的图像可知f(x)在[-1,1]上是增加的.
∴x∈[-1,1]时,f(x)min=f(-1)=-1-2+b2-b+1=b2-b-2,
令b2-b-2>0,解得b<-1或b>2.
9.若不等式-2≤x2-2ax+a≤-1有唯一解,则a的值为________.
答案
解析 若不等式-2≤x2-2ax+a≤-1有唯一解,
则x2-2ax+a=-1有两个相等的实根,
所以Δ=4a2-4(a+1)=0,解得a=.
10.设f(x)是定义在R上的以3为周期的奇函数,若f(1)>1,f(2)=,则实数a的取值范围是________.
答案 (-1,)
解析 ∵f(x+3)=f(x),
∴f(2)=f(-1+3)=f(-1)=-f(1)<-1.
∴<-1⇔<0⇔(3a-2)(a+1)<0,
∴-10,∵x≥0时,f(x)=x2-4x,∴f(-x)=(-x)2-4(-x)=x2+4x,又f(x)为偶函数,∴f(-x)=f(x),∴x<0时,f(x)=x2+4x,故有f(x)=再求f(x)<5的解,
由得0≤x<5;由
得-50的解集;
(2)若a>0,且00,
即a(x+1)(x-2)>0.
当a>0时,不等式F(x)>0的解集为{x|x<-1或x>2};
当a<0时,不等式F(x)>0的解集为{x|-10,且00.
∴f(x)-m<0,即f(x)-,解不等式(a-2b)x2+2(a-b-1)x+(a-2)>0.
解 因为(a+b)x+(2a-3b)<0,
所以(a+b)x<3b-2a,
因为不等式的解为x>-,
所以a+b<0,且=-,
解得a=3b<0,
则不等式(a-2b)x2+2(a-b-1)x+(a-2)>0
等价为bx2+(4b-2)x+(3b-2)>0,
即x2+(4-)x+(3-)<0,
即(x+1)(x+3-)<0.
因为-3+<-1,
所以不等式的解为-3+