2020年高考数学(理)二轮复习讲练测 专题09 立体几何（练）（原卷板） 5页

专题09 立体几何(练)‎ ‎1．【2019年高考全国Ⅲ卷理数】如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则( )‎ A．BM=EN，且直线BM，EN 是相交直线 B．BM≠EN，且直线BM，EN 是相交直线 C．BM=EN，且直线BM，EN 是异面直线 D．BM≠EN，且直线BM，EN 是异面直线 ‎2、【2019年高考全国Ⅰ卷理数】已知三棱锥P−ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF=90°，则球O的体积为( )‎ A． B．‎ C． D．‎ ‎3、【2019年高考浙江卷】设三棱锥V–ABC的底面是正三角形，侧棱长均相等，P是棱VA上的点(不含端点)．记直线PB与直线AC所成的角为α，直线PB与平面ABC所成的角为β，二面角P–AC–B的平面角为γ，则( )‎ A．β<γ，α<γ B．β<α，β<γ ‎ C．β<α，γ<α D．α<β，γ<β ‎ ‎4．【2019年高考全国Ⅲ卷理数】学生到工厂劳动实践，利用3D打印技术制作模型.如图，该模型为长方体挖去四棱锥O—EFGH后所得的几何体，其中O为长方体的中心，E，F，G，H分别为所在棱的中点，，3D打印所用原料密度为0.9 g/cm3，不考虑打印损耗，制作该模型所需原料的质量______g.‎ ‎ ‎ ‎5、【2019年高考北京卷理数】已知l，m是平面外的两条不同直线．给出下列三个论断：‎ ‎①l⊥m； ②m∥； ③l⊥．‎ 以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．‎ ‎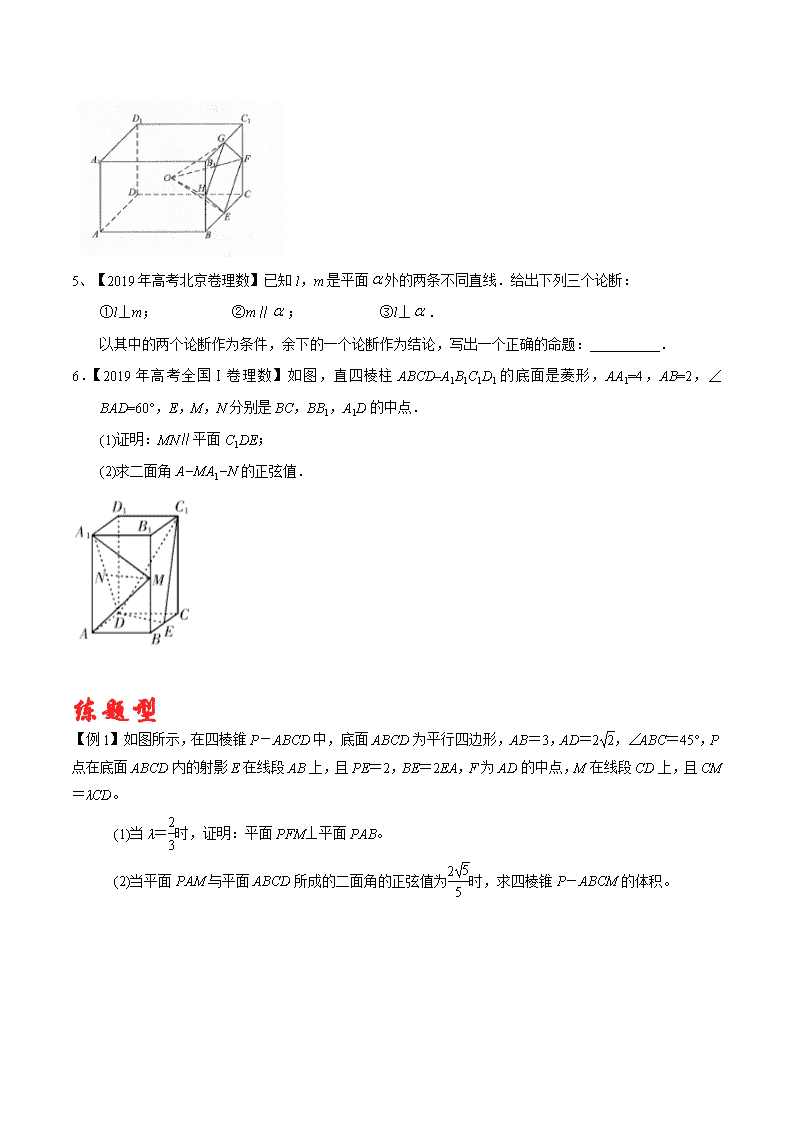6．【2019年高考全国Ⅰ卷理数】如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．‎ ‎(1)证明：MN∥平面C1DE；‎ ‎(2)求二面角A−MA1−N的正弦值．‎ ‎【例1】如图所示，在四棱锥P－ABCD中，底面ABCD为平行四边形，AB＝3，AD＝2，∠ABC＝45°，P点在底面ABCD内的射影E在线段AB上，且PE＝2，BE＝2EA，F为AD的中点，M在线段CD上，且CM＝λCD。‎ ‎(1)当λ＝时，证明：平面PFM⊥平面PAB。‎ ‎(2)当平面PAM与平面ABCD所成的二面角的正弦值为时，求四棱锥P－ABCM的体积。‎ ‎【例2】如图①所示，正△ABC的边长为4，CD是AB边上的高，E，F分别是AC和BC边的中点，现将△ABC沿CD翻折成直二面角A－DC－B，如图②所示。‎ ‎(1)试判断直线AB与平面DEF的位置关系，并说明理由。‎ ‎(2)求二面角E－DF－C的余弦值。‎ ‎(3)在线段BC上是否存在一点P，使AP⊥DE？证明你的结论。‎ ‎1、【云南省昆明市2019届高三高考5月模拟数学试题】已知直线平面，直线平面，若，则下列结论正确的是( )‎ A．或 B．‎ C． D．‎ ‎2．【陕西省2019届高三年级第三次联考数学试题】已知三棱柱的侧棱与底面边长都相等，‎ 在底面上的射影为的中点，则异面直线与所成的角的余弦值为( )‎ A． B． C． D．‎ ‎3．【四川省宜宾市2019届高三第三次诊断性考试数学试题】如图，边长为2的正方形中，分别是的中点，现在沿及把这个正方形折成一个四面体，使三点重合，重合后的点记为，则四面体的高为( )‎ A． B．‎ C． D．1‎ ‎4、【2019年高考北京卷理数】某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为1，那么该几何体的体积为__________．‎ ‎5．【2019年高考江苏卷】如图，长方体的体积是120，E为的中点，则三棱锥E−BCD的体积是 .‎ ‎6．【广东省深圳市高级中学2019届高三适应性考试(6月)数学试题】在三棱锥中，平面 平面，是边长为6的等边三角形，是以为斜边的等腰直角三角形，则该三棱锥外 接球的表面积为_______．‎ ‎7．【2019年高考浙江卷】如图，已知三棱柱，平面平面,，分别是AC，A1B1的中点.‎ ‎(1)证明：；‎ ‎(2)求直线EF与平面A1BC所成角的余弦值.‎ ‎8．【2019北京市通州区三模数学试题】如图，在四棱柱中，侧棱，，，，点为线段上的点，且．‎ ‎(1)求证：平面；‎ ‎(2)求二面角的余弦值；‎ ‎(3)判断棱上是否存在点，使得直线平面，若存在，求线段的长；若不存在，说明理由．‎