数学文卷·2018届四川省南充市高三第二次高考适应性考试（2018 10页

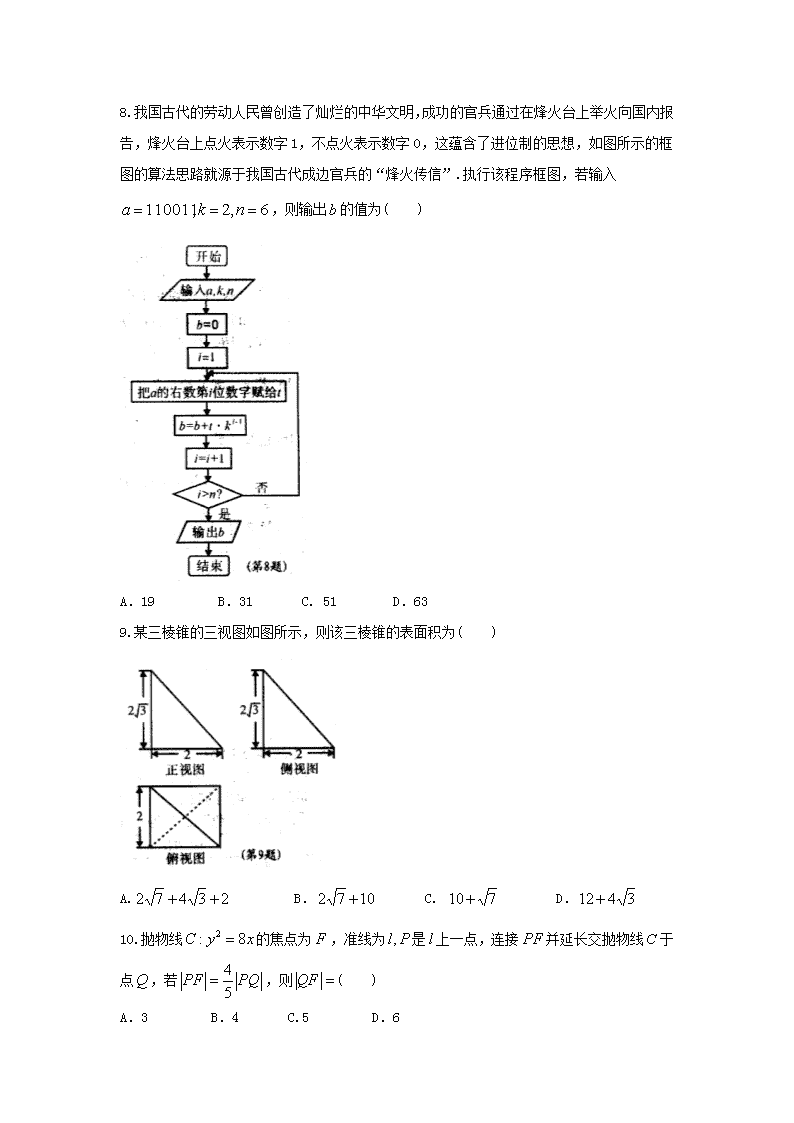
南充市高2018届第二次高考适应性考试 数学试题（文科）‎ 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知集合，，则( )‎ A． B． C． D．‎ ‎2.复数（是虚数单位）的虚部为( )‎ A． B． C． D．‎ ‎3.若函数是幂函数，且满足，则( )‎ A． B． C． D．-3 ‎ ‎4.命题“”的否定是( )‎ A． B． ‎ C. D．‎ ‎5.为了得到函数的图象，只需将的图象( )‎ A．向左平移个单位 B．向右平移个单位 ‎ C.向右平移个单位 D．向左平移个单位 ‎6.设是周期为4的奇函数，当时，，则( )‎ A． B． C. D．‎ ‎7.式子等于( )‎ A．0 B． C.-1 D．‎ ‎8.我国古代的劳动人民曾创造了灿烂的中华文明，成功的官兵通过在烽火台上举火向国内报告，烽火台上点火表示数字1，不点火表示数字0，这蕴含了进位制的思想，如图所示的框图的算法思路就源于我国古代成边官兵的“烽火传信”.执行该程序框图，若输入，则输出的值为( )‎ A．19 B．31 C. 51 D．63‎ ‎9.某三棱锥的三视图如图所示，则该三棱锥的表面积为( )‎ A. B． C. D．‎ ‎10.抛物线的焦点为，准线为是上一点，连接并延长交抛物线于点，若，则( )‎ A．3 B．4 C.5 D．6‎ ‎11.已知点为内一点，且有,记的面积分别为，则等于( )‎ A．6：1：2 B．3：1：2 C. 3：2：1 D．6：2：1‎ ‎12.在平面直角坐标系中，已知，，则的最小值为( )‎ A．1 B．2 C.3 D．4‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.已知向量，且，则实数 ．‎ ‎14.在中，若，则 ．‎ ‎15.若满足约束条件，则的最小值为 ．‎ ‎16.已知函数，函数对任意的都有成立，且与的图象有个交点为，则 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. 在等差数列中，公差，记数列的前项和为.‎ ‎(Ⅰ)求；‎ ‎(Ⅱ)设数列的前项和为，求.‎ 18. 某校开展“翻转合作学习法”教学试验，经过一年的实践后，对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试，按照大于或等于120分为“成绩优秀”，120分以下为“成绩一般”统计，得到如下的列联表：‎ 成绩优秀 成绩一般 合计 对照班 ‎20‎ ‎90‎ ‎110‎ 翻转班 ‎40‎ ‎70‎ ‎110‎ 合计 ‎60‎ ‎160‎ ‎220‎ ‎(Ⅰ)根据上面的列联表判断，能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关；‎ ‎(Ⅱ)为了交流学习方法，从这次测试数学成绩优秀的学生中，用分层抽样方法抽出6名学生，再从这6名学生中抽3名出来交流学习方法，求至少抽到1名“对照班”学生交流的概率.‎ 附表：‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎19.如图，再多面体中，是等边三角形，是等腰直角三角形，，平面平面，平面，点为的中点.‎ ‎(Ⅰ)求证：平面；‎ ‎(Ⅱ)若,求三棱锥的体积.‎ ‎20. 已知椭圆的离心率为，点在椭圆上.‎ ‎(Ⅰ)求椭圆的方程；‎ ‎(Ⅱ)直线平行于为坐标原点），且与椭圆交于两个不同的点，若为钝角，求直线在轴上的截距的取值范围.‎ ‎21.已知函数.‎ ‎(Ⅰ)若函数与的图象无公共点，求实数的取值范围；‎ ‎(Ⅱ)若存在两个实数，且，满足，求证：. ‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22.选修4-4：坐标系与参数方程 在直角坐标系中，曲线的参数方程为（其中为参数），曲线，以坐标原点为极点，以轴正半轴为极轴建立极坐标系.‎ ‎(Ⅰ)求曲线的普通方程和曲线的极坐标方程；‎ ‎(Ⅱ)若射线与曲线，分别交于两点，求.‎ ‎23.选修4-5：不等式选讲 已知函数.‎ ‎(Ⅰ)解关于的不等式；‎ ‎(Ⅱ)若关于的不等式的解集不是空集，求的取值范围.‎ 南充市高 2018 届第二次高考适应性考试 数学试题（文科）参考答案 一、选择题 ‎1-5: DCABD 6-10:DACBC 11、12：AB 二、填空题 ‎13.8 14. 15. -6 16.‎ 三、解答题 ‎17.解：（Ⅰ）由可得，‎ 又，所以.于是.‎ 则.‎ ‎（Ⅱ）因为.‎ 所以.‎ ‎18.解：（Ⅰ）‎ 所以，在犯错误的概率不超过 0.001 的前提下，不能认为“成绩优秀与翻转合作学习法”有关.‎ ‎（Ⅱ）设从“对照班”中抽取人，从“翻转班”中抽取人，由分层抽样可知：在这 6 名学生中，设“对照班”的两名学生分别为,“翻转班”的 4 名学生分别为，则所有抽样情况如下：‎ ‎,共 20 种.‎ 其中至少有一名“对照班”学生的情况有 16 种，‎ 记事件为至少抽到 1 名“对照班”学生交流，则.‎ ‎19.‎ ‎（Ⅰ）证明：∵是等腰直角三角形，‎ ‎，点为的中点，∴.‎ ‎∵ 平面平面，‎ 平面平面，‎ 平面,‎ ‎∴平面.‎ ‎∵平面，∴.‎ ‎∵平面，平面，‎ ‎∴平面.‎ ‎(Ⅱ)由(Ⅰ)知平面，‎ ‎∴点到平面的距离等于点到平面的距离.‎ ‎∵是等边三角形,点为 的中点 ‎∴‎ ‎∴‎ ‎20.解：（Ⅰ）因为椭圆的离心率为,点在椭圆上 所以，解得.‎ 故椭圆的标准方程为.‎ ‎（Ⅱ）由直线平行于得直线的斜率为,又在轴上的截距，故的方程为.‎ 由得，又直线与椭圆交于两个不同的点，‎ 设，则.‎ 所以，于是.‎ 为钝角等价于,且 则 即，又，所以的取值范围为.‎ ‎21.解：（Ⅰ）因为函数与的图象无公共点，所以方程 无实数解，‎ 即无实数解，令，.‎ 当时，，当时，‎ 在单增，在单减，‎ 故时，取得极大值，也为最大值.‎ 所以，实数的取值范围.‎ ‎（Ⅱ）证明：令，因为.‎ 所以.‎ 则，.‎ 所以等价于，即，‎ 即，‎ 令，则等价于，‎ 令.‎ 所以在上递增, 即有，‎ 即成立，故.‎ ‎22.解：（Ⅰ）由得，‎ 所以曲线的普通方程为.‎ 把，代入，得到，化简得到曲线的极坐标方程为.‎ ‎（Ⅱ）依题意可设,曲线的极坐标方程为.‎ 将代入的极坐标方程得，解得.‎ 将代入的极坐标方程得.‎ 所以.‎ ‎23.解：（Ⅰ）由可得.‎ 所以或或 于是或，‎ 即.所以原不等式的解集为.‎ ‎（Ⅱ）由条件知，不等式有解，则即可.‎ 由于，‎ 当且仅当，即当时等号成立，故.‎ 所以，的取值范围是.‎