江西省上饶中学2018-2019学年高二（实验、重点、体艺班）上学期第一次月考数学（理）试卷（理科实验、重点） 9页

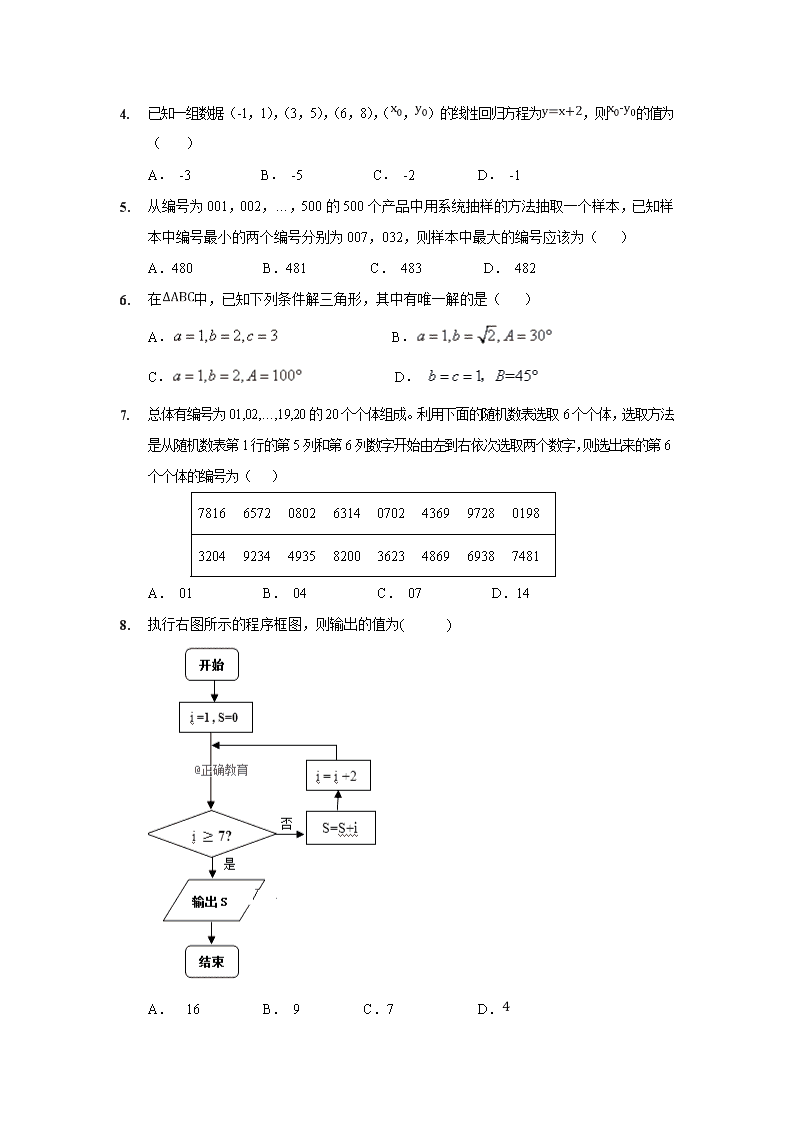
上饶中学2018-2019学年高二上学期第一次月考 数 学 试 卷（理科实验、重点班）‎ 命题人：章 琪 考试时间：120分钟 分值：150分 一、选择题(本大题共12小题，每小题5分，共60分)‎ 1. 若，则下列不等式成立的是（ ）‎ A． B． C． D．‎ 2. 某班级有男生20人，女生30人，从中抽取10人作为样本，其中一次抽样结果是：抽到了4名男生、6名女生，则下列命题正确的是（ ）‎ A．这次抽样中每个女生被抽到的概率大于每个男生被抽到的概率 ‎ B．这次抽样中每个女生被抽到的概率小于每个男生被抽到的概率 C．这次抽样一定没有采用系统抽样 D．这次抽样可能采用的是简单随机抽样 3. 如右饼图，某学校共有教师120人，从中选出一个30人的样本，其中被选出的青年女教师的人数为（　　）‎ A． 3 ‎ B． 4 ‎ C． 6 ‎ D． 12‎ 1. 已知一组数据（-1，1），（3，5），（6，8），（，）的线性回归方程为，则的值为（　　）‎ A． -3 B． -5 C． -2 D． -1‎ 2. 从编号为001，002，…，500的500个产品中用系统抽样的方法抽取一个样本，已知样本中编号最小的两个编号分别为007，032，则样本中最大的编号应该为（ ）‎ A．480 B．481 C． 483 D． 482‎ 3. 在中，已知下列条件解三角形，其中有唯一解的是（ ）‎ A． B．‎ C． D． ‎ 4. 总体有编号为01,02,…,19,20的20个个体组成。利用下面的随机数表选取6个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第6个个体的编号为（ ）‎ ‎7816 6572 0802 6314 0702 4369 9728 0198‎ ‎3204 9234 4935 8200 3623 4869 6938 7481‎ A． 01 B． 04 C． 07 D．14‎ 5. 执行右图所示的程序框图，则输出的值为( ) ‎ A． 16 B． 9 C．7 D．‎ 1. 在中，角A、B、C所对的边分别为a、b、c，且 若  ，则的形状是　　‎ A． 等边三角形 B． 直角三角形 ‎ C． 等腰三角形 D． 等腰直角三角形 2. 定义算式：，若不等式对任意都成立，则实数的取值范围是（　　）．‎ A． B． C． D． ‎ 3. 已知的三边长分别为a,b,c,且满足b+c3a，则的取值范围为（　　）．‎ A． B． C． D．‎ 4. 设点为区域内任意一点，则使函数在区间上是增函数的概率为（　　）．‎ A． B． C． D． ‎ 二、填空题（本大题共4小题，每题5分，共20分）‎ 5. 不等式的解集为__________．‎ 6. 已知点，点满足线性约束条件 ，为坐标原点，那么的最小值为_______________．‎ 7. 在正六边形的6个顶点中随机选取4个顶点，则构成的四边形是梯形的概率为_______________．‎ 8. 已知二次函数f（x）=ax2+2x+c（x∈R）的值域为[0，+∞），则的最小值为_____．‎ 三、解答题（本大题共6小题，共70分）‎ 9. ‎(10分)利用基本不等式求最值。‎ ‎（1）已知求函数的最小值．‎ （2） 已知，求函数的最大值．‎ 使用年数 ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ 销售价格 ‎16‎ ‎13‎ ‎9.5‎ ‎7‎ ‎4.5‎ 1. ‎(12分)某二手交易市场对某型号的二手汽车的使用年数与销售价格（单位：万元/辆）进行整理，得到如下的对应数据： ‎ ‎（Ⅰ）试求关于的回归直线方程 ‎（参考公式：，）‎ ‎（Ⅱ）已知每辆该型号汽车的收购价格为万元，根据（Ⅰ）中所求的回归方程，预测为何值时，销售一辆该型号汽车所获得的利润最大？（利润=销售价格-收购价格）‎ 2. ‎(12分)如图，在中，点边上， , ‎ ‎（Ⅰ）求的面积．‎ ‎（Ⅱ）若，求的长．‎ 3. ‎(12分)某车间将名技工平均分成甲、乙两组加工某种零件，在单位时间内每个技工加工的合格零件数的茎叶图如图，已知两组技工在单位时间内加工的合格零件的平均数都为.‎ ‎（1）求的值；‎ ‎（2）求甲、乙两组技工在单位时间内加工的合格零件的方差，并由此分析两组技工的加工水平；‎ ‎（3）质检部门从该车间甲、乙两组技工中各随机抽取一名，对其加工的零件进行检测，若两人加工的合格零件个数之和大于，则称该车间“质量合格”，求该车间“质量合格”的概率.‎ 1. ‎ (12分)某班100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100]． ‎ 分数段 ‎[50,60)‎ ‎[60,70)‎ ‎[70,80)‎ ‎[80,90)‎ x∶y ‎1∶1‎ ‎2∶1‎ ‎3∶4‎ ‎4∶5‎ ‎ ‎ ‎(1)求图中a的值；‎ ‎(2)根据频率分布直方图，估计这100名学生语文成绩的平均分；‎ ‎(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如上表所示，求数学成绩在[50,90)之外的人数．‎ 2. ‎(12分)已知函数．‎ ‎（1）解不等式；‎ ‎（2）若函数在区间上存在零点，求实数的取值范围；‎ ‎（3）若函数，其中为奇函数，为偶函数，若不等式对任意恒成立，求实数的取值范围．‎ 参考答案 ‎1．B 2．D 3．A 4．C 5．D ‎6．D 7．B 8．B 9．A 10．C ‎11．D ‎12．B ‎13．‎ ‎14．-3‎ ‎15．‎ ‎16．4‎ ‎17．（1）‎ 当且仅当即时，等号成立，故函数的最小值为6‎ ‎（2） ，，则 当且仅当即时，‎ ‎18．（Ⅰ）由由表中数据，计算，‎ ‎，‎ ‎ ；‎ ‎，‎ 由最小二乘法求得，‎ ‎，‎ 关于的回归直线方程为；‎ ‎（Ⅱ）根据题意利润函数为 ‎ ‎ 当时，利润取得最大值．‎ ‎19．（Ⅰ）由题意，‎ 在中，由余弦定理可得 即或（舍）,‎ ‎∴的面积.‎ ‎（Ⅱ）在中，由正弦定理得，‎ 代入得，由为锐角，故 ,‎ 所以,‎ 在中，由正弦定理得，‎ ‎∴，解得.‎ ‎20．详解：（1）根据题意可知：，‎ ‎，‎ 解得，.‎ ‎（2），‎ ‎，‎ ‎∵，，‎ ‎∴甲、乙两组的整体水平相当，乙组更稳定一些.‎ ‎（3）质检部门从该车间甲、乙两组技工中各随机抽取一名，对其加工的零件进行检测，设两人加工的合格零件数分别为，，则所有的可能为，，，，，，，，，，，，，，，，，，，，，，，，，共计个.‎ 而的基本事件有，，，，，共计个，‎ 故满足的基本事件共有（个），‎ 故该车间“质量合格”的概率为.‎ ‎21．(1)由频率分布直方图知(2a＋0.02＋0.03＋0.04)×10＝1，解得a＝0.005．‎ ‎(2)由频率分布直方图知这100名学生语文成绩的平均分为55×0.005×10＋65×0.04×10＋75×0.03×10＋85×0.02×10＋95×0.005×10＝73(分)．‎ ‎(3)由频率分布直方图知语文成绩在[50,60)，[60,70)，[70,80)，[80,90)各分数段的人数依次为0.005×10×100＝5；0.04×10×100＝40；0.03×10×100＝30；0.02×10×100＝20．‎ 由题中给出的比例关系知数学成绩在上述各分数段的人数依次为5；40×＝20；30×＝40；20×＝25．‎ 故数学成绩在[50,90)之外的人数为100－(5＋20＋40＋25)＝10．‎ ‎22．（1）原不等式即为，设t=2x，则不等式化为t﹣t2＞16﹣9t，‎ 即t2﹣10t+16＜0，解得2＜t＜8，即2＜2x＜8，∴1＜x＜3，∴原不等式的解集为（1，3）．‎ ‎（2）函数在上有零点，∴在上有解，即在有解．‎ 设，∵，∴，‎ ‎∴当时，；当时，，∴．‎ ‎∵在有解，∴，故实数m的取值范围为．‎ ‎（3）由题意得，解得．‎ 由题意得，即 对任意恒成立，令，则．‎ 则得对任意的恒成立，∴对任意的恒成立，∵在上单调递减，∴．‎ ‎∴，∴实数的取值范围．‎