上海市17区县2013届高三一模（数学理科）分类汇编：专题十二 应用题 7页

专题十二 应用题 ‎2013年2月 ‎（杨浦区2013届高三一模 理科）12．如图，已知边长为‎8米的正方形钢板有一个角锈蚀，‎ ‎ 其中米，米. 为了合理利用这块钢板,将在五边 ‎ 形内截取一个矩形块，使点在边上. ‎ ‎ 则矩形面积的最大值为____ 平方米 . 12． 48；‎ ‎（松江区2013届高三一模 理科）21．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分 ‎“活水围网”养鱼技术具有养殖密度高、经济效益好的特点．研究表明：“活水围网”养鱼时，某种鱼在一定的条件下，每尾鱼的平均生长速度（单位：千克/年）是养殖密度（单位：尾/立方米）的函数．当不超过4（尾/立方米）时，的值为（千克/年）；当时，是的一次函数；当达到（尾/立方米）时，因缺氧等原因，的值为（千克/年）。‎ ‎（1）当时，求函数的表达式；‎ ‎（2）当养殖密度为多大时，鱼的年生长量（单位：千克/立方米）可以达到最大，并求出最大值．‎ ‎21．解：（1）由题意：当时，； …………………………2分 当时，设，显然在是减函数，‎ 由已知得，解得 …………………………4分 故函数= …………………………6分 ‎（2）依题意并由（1）可得 ………8分 当时，为增函数，故； …………10分 当时，，‎ ‎． …………………………12分 所以，当时，的最大值为． ‎ 当养殖密度为10尾/立方米时，鱼的年生长量可以达到最大，最大值约为千克/立方米．‎ ‎ ‎ ‎（浦东新区2013届高三一模 理科）20．（本小题满分14分，第1小题满分6分，第2小题满分8分）‎ 世博中学为了落实上海市教委推出的“阳光运动一小时”活动，计划在一块直角三角形的空地上修建一个占地面积为的矩形健身场地，如图点M在上，点N在上，且P点在斜边上，已知且米，，.‎ ‎（1）试用表示，并求的取值范围；‎ ‎（2）设矩形健身场地每平方米的造价为，再把矩形以外（阴影部分）铺上草坪， ‎ ‎ 每平方米的造价为（为正常数），求总造价关于的函数；‎ ‎ 试问如何选取的长使总造价最低（不要求求出最低造价）.‎ 解：（1）在中，显然，，‎ ‎，………………2分 ‎ 矩形的面积，…4分 于是为所求.……………………………6分 ‎（2） 矩形健身场地造价 ……………………7分 又的面积为，即草坪造价，……………8分 由总造价，，.…10分 ‎，……………………………………………………11分 当且仅当即时等号成立，……………………………12分 此时，解得或，‎ 所以选取的长为‎12米或‎18米时总造价最低.………………………14分 ‎（黄浦区2013届高三一模 理科）21．（本题满分14分）本题共有2个小题，第1小题满分8分，第2小题满分6分．‎ 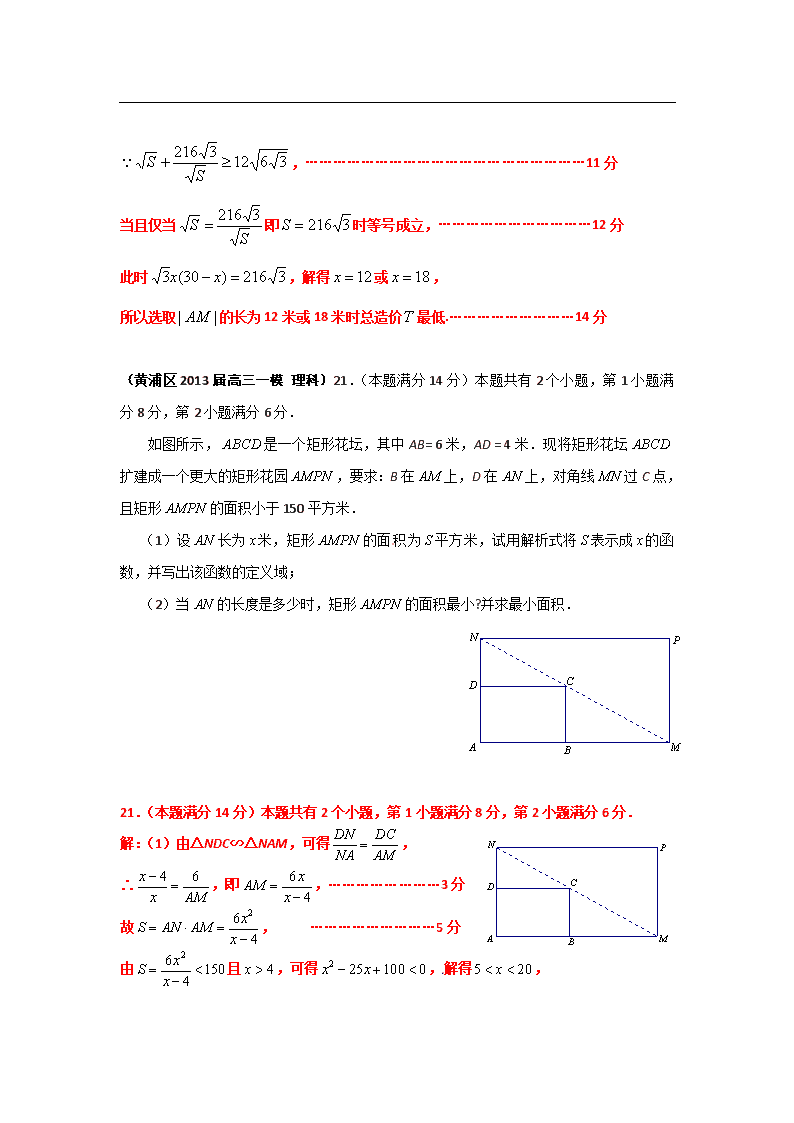如图所示，是一个矩形花坛，其中AB= ‎6米，AD = ‎4米．现将矩形花坛扩建成一个更大的矩形花园，要求：B在上，D在上，对角线过C点， 且矩形的面积小于‎150平方米． ‎ ‎（1）设长为米，矩形的面积为平方米，试用解析式将表示成的函数，并写出该函数的定义域；[来源:Zxxk.Com]‎ ‎（2）当的长度是多少时，矩形的面积最小?并求最小面积．[来源:学#科#网]‎ ‎21．（本题满分14分）本题共有2个小题，第1小题满分8分，第2小题满分6分．‎ 解：（1）由△NDC∽△NAM，可得，‎ ‎∴，即，……………………3分 故， ………………………5分 由且，可得，解得，‎ 故所求函数的解析式为，定义域为． …………………………………8分 ‎（2）令，则由，可得，‎ 故 …………………………10分 ‎， …………………………12分 当且仅当，即时．又，故当时，取最小值96．‎ 故当的长为时，矩形的面积最小，最小面积为平方米． …………14分 ‎（长宁区2013届高三一模）21、（本题满分14分）（理）经过统计分析，公路上的车流速度（单位：千米/小时）是车流密度（单位：辆/千米）的函数，当公路上的车流密度达到200辆/千米时，造成堵塞，此时车速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时，研究表明：当时，车流速度是车流密度的一次函数.‎ ‎(1)当时，求函数的表达式；‎ ‎(2)当车流密度为多大时，车流量（单位时间内通过公路上某观测点的车辆数，单位：辆/小时）可以达到最大，并求出最大值.（精确到1辆/小时）‎ ‎（文）某工厂生产一种产品的原材料费为每件40元，若用x表示该厂生产这种产品的总件数，则电力与机器保养等费用为每件0.05x元，又该厂职工工资固定支出12500元。‎ ‎ （1）把每件产品的成本费P（x）（元）表示成产品件数x的函数，并求每件产品的最低成本费；‎ ‎ （2）如果该厂生产的这种产品的数量x不超过3000件，且产品能全部销售，根据市场调查：每件产品的销售价Q（x）与产品件数x有如下关系：，试问生产多少件产品，总利润最高？（总利润=总销售额-总的成本）‎ ‎21、（理）解（1）由题意：当时，；‎ 当时，设 …………………………2分 ‎ 再由已知得解得 …………………………4分 ‎ ‎ 故函数v(x)的表达式为………………7分 ‎（2）依题意并由（1）可得， …………9分 ‎ 当时，为增函数.故当x=20时，其最大值为60×20=1200；‎ ‎ 当时，‎ ‎ 当且仅当，即时，等号成立. ‎ ‎ 所以，当时，在区间[20，200]上取得最大值. …12分 ‎ 综上，当时，在区间[0，200]上取得最大值. ‎ 即当车流密度为100辆/千米时，车流量可以达到最大，最大值约为3333辆/小时. ‎ ‎ …………………………14分 ‎（文）解：（1） ………………………………………3分 ‎ 由基本不等式得 ‎ ‎ 当且仅当，即时，等号成立 ……………………6分 ‎∴，成本的最小值为元． ……………………7分 ‎（2）设总利润为元，则 ‎ ……………10分 ‎ ‎ 当时, ……………………………………………………13分 答：生产件产品时，总利润最高，最高总利润为元．… ……14分 ‎（奉贤区2013届高三一模）21、某海域有、两个岛屿，岛在岛正东4海里处。经多年观察研究发现，某种鱼群洄游的路线是曲线，曾有渔船在距岛、岛距离和为8海里处发现过鱼群。以、所在直线为轴，的垂直平分线为轴建立平面直角坐标系。‎ ‎（1）求曲线的标准方程；（6分）‎ ‎（2）某日，研究人员在、两岛同时用声纳探测仪发出不同频率的探测信号（传播速度相同），、两岛收到鱼群在处反射信号的时间比为，问你能否确定处的位置（即点的坐标）？（8分）‎ ‎[来源:Zxxk.Com]‎ ‎21、解（1）由题意知曲线是以、为焦点且长轴长为8的椭圆 3分 ‎ 又，则，故 5分 ‎ 所以曲线的方程是 6分 ‎（2）由于、两岛收到鱼群发射信号的时间比为，‎ 因此设此时距、两岛的距离分别比为 7分 即鱼群分别距、两岛的距离为5海里和3海里。 8分 设，，由 ， 10分 ‎， 12分 ‎ ‎ 13分 点的坐标为或 14分