人教版高三数学总复习第六章单元质量检测 11页

第六章单元质量检测 时间：90分钟　分值：100分 一、选择题(每小题4分，共40分)‎ ‎1．若x>0，y>0，则“x＋y>1”是“x2＋y2>1”的(　　)‎ A．充分非必要条件 B．必要非充分条件 C．充要条件 D．非充分非必要条件 解析：在平面坐标系中，画出x＋y>1与x2＋y2>1表示的图形区域，可知x2＋y2>1成立可以得到x＋y>1成立，反过来则不成立，所以“x＋y>1”是“x2＋y2>1”的必要非充分条件，故选B.‎ 答案：B ‎2．设a，b∈R，若a－|b|>0，则下列不等式中正确的是(　　)‎ A．b－a>0 B．a3＋b3<0‎ C．a2－b2<0 D．b＋a>0‎ 解析：由a－|b|>0得a>|b|≥0，‎ 所以a>0且a＋b>0，故选D.‎ 答案：D ‎3．函数y＝(x>1)的最小值是(　　)‎ A．2＋2 B．2－2‎ C．2 D．2‎ 解析：由y＝＝ ‎＝(x＋1)＋＝(x－1)＋＋2≥2＋2.‎ 等号成立的条件是x＝1＋.‎ 答案：A ‎4．条件p：<2x<16，条件q：(x＋2)(x＋a)<0，若p是q的充分而不必要条件，则a的取值范围是(　　)‎ A．(4，＋∞) B．[－4，＋∞)‎ C．(－∞，－4] D．(－∞，－4)‎ 解析：由<2x<16，得2－2<2x<24，即－24得a<－4，故选D.‎ 答案：D ‎5．已知x，y满足则z＝x－y的取值范围是(　　)‎ A．[－，1] B．[－1,1]‎ C．[－，] D．[－1，]‎ 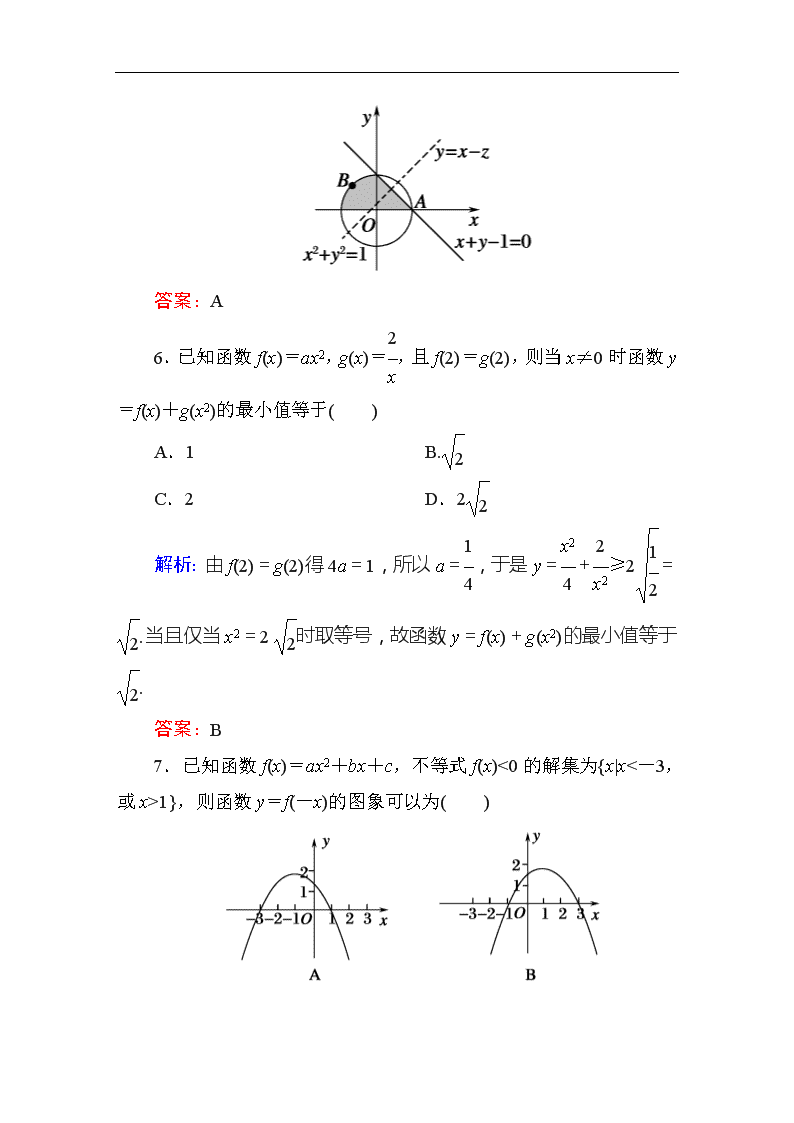解析：因为x，y满足所以得到可行域如图阴影部分所示，目标函数y＝x－z过点A(1,0)时在y轴的截距最小，此时zmax＝1；过点B时，目标函数在y轴的截距最大，此时zmin＝－最小．所以z∈[－，1]．‎ 答案：A ‎6．已知函数f(x)＝ax2，g(x)＝，且f(2)＝g(2)，则当x≠0时函数y ‎＝f(x)＋g(x2)的最小值等于(　　)‎ A．1 B. C．2 D．2 解析：由f(2)＝g(2)得4a＝1，所以a＝，于是y＝＋≥2＝.当且仅当x2＝2时取等号，故函数y＝f(x)＋g(x2)的最小值等于.‎ 答案：B ‎7．已知函数f(x)＝ax2＋bx＋c，不等式f(x)<0的解集为{x|x<－3，或x>1}，则函数y＝f(－x)的图象可以为(　　)‎ 解析：由f(x)<0的解集为{x|x<－3，或x>1}知a<0，y＝f(x)的图象与x轴交点为(－3,0)，(1,0)，∴f(－x)图象开口向下，与x轴交点为(3,0)，(－1,0)．‎ 答案：B ‎8．在平面内，设半径分别为r1，r2的两个圆相离且圆心距为d，若点M，N分别在两个圆的圆周上运动，则|MN ‎|的最大、最小值分别为d＋r1＋r2和d－r1－r2，若空间中，设半径分别为R1，R2的两个球相离且球心距为d，若点M，N分别在两个球的球面上运动，则|MN|的最大、最小值分别为(　　)‎ A．d－R1－R2和d＋R1＋R2‎ B．d＋R1＋R2和d－R1－R2‎ C．d－R1＋R2和d＋R1－R2‎ D．R1＋R2－d和0‎ 解析：因为在由平面图形到空间图形的类比推理中，圆对应球．“在平面内，设半径分别为r1，r2的两个圆相离且圆心距为d，若点M，N分别在两个圆的圆周上运动，则|MN|的最大、最小值分别为d＋r1＋r2和d－r1－r2”，我们可类比推理出：“在空间中，设半径分别为R1，R2的两个球相离且球心距为d，若点M，N分别在两个球的球面上运动，则|MN|的最大、最小值分别为d＋R1＋R2和d－R1－R2”．‎ 答案：B ‎9．将正奇数按如图所示的规律排列，则第21行从左向右的第5个数为(　　)‎ ‎1‎ ‎3　5　7‎ ‎9　11　13　15　17‎ ‎19　21　23　25　27　29　31‎ ‎…　　…　　…‎ A．809 B．852‎ C．786 D．893‎ 解析：前20行共有正奇数1＋3＋5＋…＋39＝202＝400个，则第21行从左向右的第5个数是第405个正奇数，所以这个数是2×‎ ‎405－1＝809.‎ 答案：A ‎10．已知函数f(x)＝x2，g(x)＝x－m，当x∈[1,2]时，不等式f(x)≥g(x)恒成立，则实数m的取值范围是(　　)‎ A. B. C．(3，＋∞) D．(4，＋∞)‎ 解析：不等式f(x)≥g(x)，即x2≥x－m，因此m≥x－x2.令h(x)＝x－x2，由于h(x)在[1,2]上单调递减，所以h(x)的最大值是h(1)＝－，因此实数m的取值范围是.‎ 答案：B 二、填空题(每小题4分，共16分)‎ ‎11．已知关于x的不等式ax2＋2x＋c>0的解集为，则不等式－cx2＋2x－a>0的解集为________．‎ 解析：由ax2＋2x＋c>0的解集为知a<0，且－，为方程ax2＋2x＋c＝0的两个根，由根与系数的关系得－＋＝－，×＝，解得a＝－12，c＝2，∴－cx2＋2x－a>0，即2x2－2x－12<0，其解集为(－2,3)．‎ 答案：(－2,3)‎ ‎12．给出下列等式：＝2cos，＝2cos，＝2cos ，请从中归纳出第n个等式：＝________.‎ 答案：2cos ‎13．已知O为坐标原点，A(1,2)，点P的坐标(x，y)满足约束条件则z＝·的最大值为________．‎ 解析：作可行域如图阴影部分所示，z＝·＝x＋2y，显然在B(0,1)处zmax＝2.‎ 答案：2‎ ‎14．(2014·辽宁卷)对于c>0，当非零实数a，b满足4a2－2ab＋4b2－c＝0且使|2a＋b|最大时，－＋的最小值为________．‎ 解析：要求|2a＋b|最大值，只需求(2a＋b)2的最大值．‎ ‎∵4a2－2ab＋4b2－c＝0，‎ ‎∴4a2＋b2＝c＋2ab－3b2.‎ ‎∴(2a＋b)2＝4a2＋b2＋4ab＝c＋2ab－3b2＋4ab＝c＋6ab－3b2＝c＋3b(2a－b)＝c＋·2b(2a－b)≤c＋2＝c＋2.‎ 即(2a＋b)2≤c，当且仅当2b＝2a－b，即3b＝2a时取到等号，即(2a＋b)2取到最大值．‎ 故3b＝2a时，|2a＋b|取到最大值．‎ 把3b＝2a时，即b＝代入4a2－2ab＋4b2－c＝0，可得c＝a2.‎ ‎∴－＋＝－＋＝－＋＝＝2－2.‎ ‎∴当＝时，－＋取到最小值－2.‎ 答案：－2‎ 三、解答题(共4小题，共44分，解答应写出必要的文字说明、计算过程或证明步骤．)‎ ‎15．(10分)已知x>0，y>0，且2x＋5y＝20.‎ ‎(1)求u＝lgx＋lgy的最大值；‎ ‎(2)求＋的最小值．‎ 解：(1)∵x>0，y>0，‎ ‎∴由基本不等式，得2x＋5y≥2.‎ ‎∵2x＋5y＝20，‎ ‎∴2≤20，xy≤10，当且仅当2x＝5y时，等号成立．‎ 因此有解得 此时xy有最大值10.‎ ‎∴u＝lgx＋lgy＝lg(xy)≤lg10＝1.‎ ‎∴当x＝5，y＝2时，u＝lgx＋lgy有最大值1.‎ ‎(2)∵x>0，y>0，‎ ‎∴＋＝·＝≥＝，‎ 当且仅当＝时，等号成立．‎ 由解得 ‎∴＋的最小值为.‎ ‎16．(10分)已知等差数列{an}的公差d＝2，首项a1＝5.‎ ‎(1)求数列{an}的前n项和Sn；‎ ‎(2)设Tn＝n(2an－5)，求S1，S2，S3，S4，S5；T1，T2，T3，T4，T5，并归纳出Sn与Tn的大小规律．‎ 解：(1)由于a1＝5，d＝2，‎ ‎∴Sn＝5n＋×2＝n(n＋4)．‎ ‎(2)∵Tn＝n(2an－5)＝n[2(2n＋3)－5]＝4n2＋n.‎ ‎∴T1＝5，T2＝4×22＋2＝18，T3＝4×32＋3＝39，‎ T4＝4×42＋4＝68，T5＝4×52＋5＝105.‎ S1＝5，S2＝2×(2＋4)＝12，S3＝3×(3＋4)＝21，‎ S4＝4×(4＋4)＝32，S5＝5×(5＋4)＝45.‎ 由此可知S1＝T1，当n≥2时，Snx，求实数a的取值范围；‎ ‎(3)已知a<1，c1>0，且cn＋1＝f′(cn)(n＝1,2，…)，证明：数列{cn}是单调递增数列．‎ 解：(1)当a＝2时，f(x)＝x2－2x＋ln(x＋1)，‎ f′(x)＝2x－2＋＝，‎ 令f′(x)＝0，得x＝±.‎ 又x>－1，且x∈(－1，－)∪(，＋∞)时，f′(x)>0，x∈(－，)时，f′(x)<0，‎ ‎∴函数f(x)的极大值点为x＝－，极小值点为x＝.‎ ‎(2)∵f′(x)＝2x－a＋，由f′(x)>x，得2x－a＋>x，即a1，∴a≤1.‎ ‎(3)①当n＝1时，c2＝f′(c1)＝2c1－a＋，‎ ‎∵c1>0，∴c1＋1>1，又a<1，‎ ‎∴c2－c1＝c1－a＋＝c1＋1＋－(a＋1)>2－(a＋1)＝1－a ‎>0，‎ ‎∴c2>c1，即当n＝1时结论成立．‎ ‎②假设当n＝k(k∈N*)时，有ck＋1>ck>0.‎ 则当n＝k＋1时，ck＋2－ck＋1＝ck＋1－a＋＝ck＋1＋1＋－(a＋1)>2－(a＋1)＝1－a>0.‎ ‎∴ck＋2>ck＋1，即当n＝k＋1时结论成立．‎ 由①，②知数列{cn}是单调递增数列．‎