2017-2018学年辽宁省六校协作体高二下学期期初考试数学（理）试题（Word版） 10页

‎2017-2018学年辽宁省六校协作体高二下学期期初考试 数学（理科）‎ 命题学校：东港市第二中学命题人： 阮征 校对人：任明刚 第Ⅰ卷（共60分）‎ 一 选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎（1）若集合A={x|x2+5x+4＜0}，集合B={x|x＜﹣2}，则A∩（∁RB）等于（　　）‎ A．（﹣2，﹣1） B．[﹣2，4） C．[﹣2，﹣1） D．‎ ‎（2）抛物线的焦点坐标是 A. B. C. D. ‎ ‎（3）已知向量，，，若与共线，则的值为（　　）‎ A.4 B‎.8 C.0 D.2‎ ‎（4）已知平面α∩平面β=m，直线l⊂α，则“l⊥m”是“l⊥β”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎（5）已知函数的图象经过定点，若幂函数的图象过点，则的值等于 A. B. C. 2 D. 3‎ ‎（6）几何体的三视图如图，则该几何体的体积是 A． B． C． D．‎ ‎（7）设数列的前项和,‎ A. 124 B. ‎120 C. 128 D. 121‎ ‎（8）双曲线离心率为，左右焦点分别为为双曲线右支上一点，的平分线为，点关于的对称点为,，则双曲线方程为（ ）‎ A. B. C. D. ‎ ‎（9）已知，，则的值为（）‎ A. B. C. D.‎ ‎（10）在中，，边上的高等于,则（ ）‎ A. B. C. D. ‎ ‎（11）已知在矩形中，，在其中任取一点，满足的概率为（ ）‎ A． B． C． D．不确定 ‎（12）设椭圆与直线相交于，两点，若在椭圆上存在点，使得直线，斜率之积为，则椭圆离心率为（ ）‎ A． B． C． D． 二 填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎（13）函数的部分图象如图所示，则将的图象向右平移个单位后，得到的图象对应的函数解析式 为__ __.‎ ‎（14）已知，并且成等差数列，则的最小值为_ __.‎ ‎（15）已知三棱锥中，，，，，，则三棱锥的外接球的表面积为__________．‎ ‎（16）函数，且，，则的取值范围是__________．‎ 三 解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎（17）（本小题满分10分）‎ 已知函数（其中），若的一条对称轴离最近的对称中心的距离为 ‎（I）求的单调递增区间；‎ ‎（II）在中角A、B、C的对边分别是满足恰是的最大值，试判断的形状.‎ ‎（18）（本小题满分12分）‎ 某高中有高一新生500名，分成水平相同的两类教学实验，为对比教学效果，现用分层抽样的方法从两类学生中分别抽取了40人，60人进行测试 ‎（1）求该学校高一新生两类学生各多少人？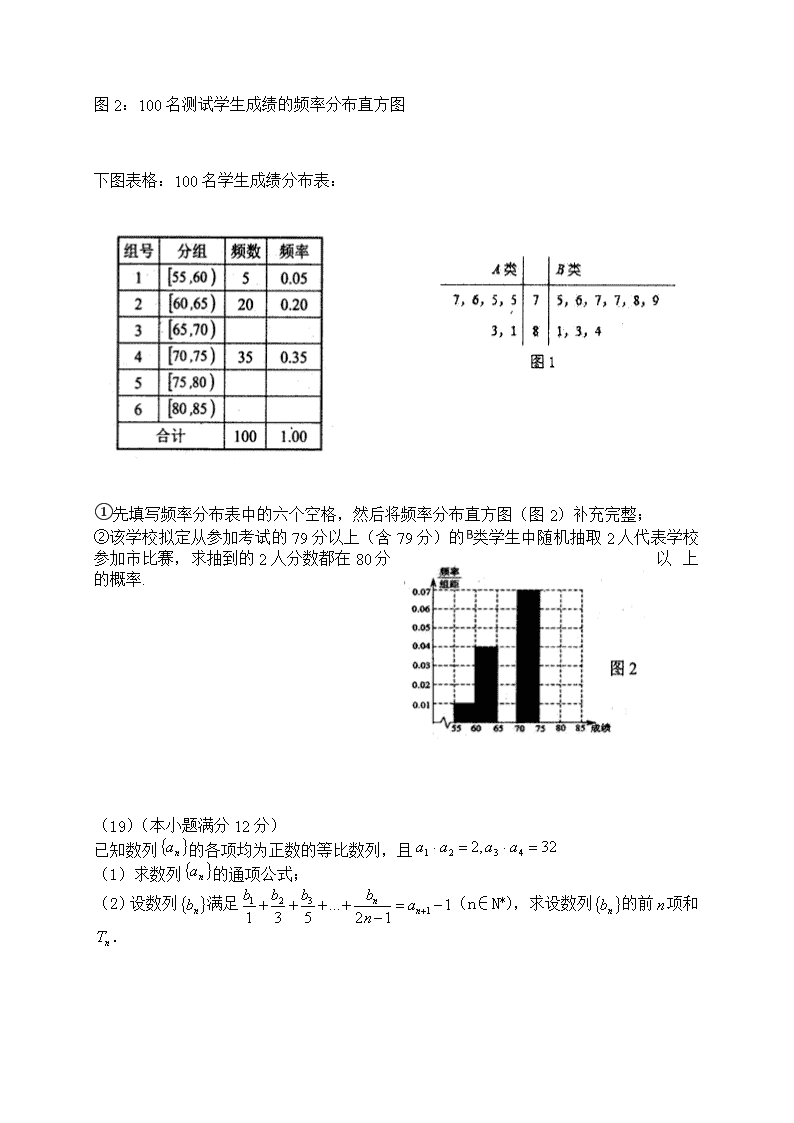‎ ‎（2）经过测试，得到以下三个数据图表：‎ 图1：75分以上两类参加测试学生成绩的茎叶图 图2：100名测试学生成绩的频率分布直方图 下图表格：100名学生成绩分布表：‎ ‎①先填写频率分布表中的六个空格，然后将频率分布直方图（图2）补充完整；‎ ‎②该学校拟定从参加考试的79分以上（含79分）的类学生中随机抽取2人代表学校参加市比赛，求抽到的2人分数都在80分以上的概率.‎ ‎（19）（本小题满分12分）‎ 已知数列的各项均为正数的等比数列，且 ‎（1）求数列的通项公式；‎ ‎（2）设数列满足（n∈N*），求设数列的前项和.‎ ‎（20）（本小题满分12分）‎ 在如图所示的几何体中，正方形所在的平面与正三角形ABC所在的平面互相垂直，，且，是的中点．‎ ‎（1）求证：∥平面；‎ ‎（2）求二面角的余弦值．‎ ‎（21）（本小题满分12分）已知圆的圆心在坐标原点，且与直线相切.‎ ‎（1）求直线被圆C所截得的弦AB的长；‎ ‎（2）过点作两条与圆相切的直线，切点分别为，求直线的方程；‎ ‎（3）若与直线垂直的直线不过点，且与圆C交于不同的两点.若为钝角，求直线的纵截距的取值范围．‎ ‎（22）（本小题满分12分）已知抛物线C：的焦点为F，直线与y轴的交点为P，与C的交点为Q，且.‎ ‎（1）求C的方程；‎ ‎（2）过F的直线与C相交于A，B两点，若AB的垂直平分线与C相较于M，N两点，且A，M，B，N四点在同一圆上，求的方程.‎ ‎2017-2018学年度下学期省六校协作体高二期初考试理科数学答案 选择题：‎1C 2B ‎3A 4B 5B ‎6C 7D ‎8C ‎9A ‎10C ‎11A 12B 填空题：13 14 16 15 16 ‎ 解答题：17解：(Ⅰ)因为 的对称轴离最近的对称中心的距离为所以，所以，所以 ‎………………………………3分 解 得：‎ 所以函数单调增区间为……………………5分 ‎(Ⅱ) 因为，由正弦定理，‎ 得 因为 ‎，所以 所以，所以……………………8分 所以 根据正弦函数的图象可以看出，无最小值,有最大值，‎ 此时，即,所以所以为等边三角形…………………………10分 ‎18解：（1）由题意知A类学生有（人）则B类学生有500－200=300（人）. …2分 ‎（2）①表一 ‎…………………5分 图二 组号 分组 频数 频率 ‎1‎ ‎5‎ ‎0.05‎ ‎2‎ ‎20‎ ‎0.20‎ ‎3‎ ‎25‎ ‎0.25‎ ‎4‎ ‎35‎ ‎0.35‎ ‎5‎ ‎10‎ ‎0.10‎ ‎6‎ ‎5‎ ‎0.05‎ 合计 ‎100‎ ‎1.00‎ ‎…………………8分 ‎②79分以上的B类学生共4人，记80分以上的三人分别是，79分的学生为.‎ 从中抽取2人，有（12）、（13）、（‎1a）、（23）、（‎2a）、（‎3a）共6种抽法；‎ 抽出2人均在80分以上有：（12）、（13）、（23）共3种抽法 则抽到2人均在80分以上的概率为…………………12分 ‎19（1）设等比数列的公比为，由已知得2分 又∵，解得3分 ∴； 5分 ‎（2）由题意可得①‎ ‎ ②‎ 相减得，，（） 7分 当时，，符合上式， 8分 设 则，‎ 两式相减得：‎ ‎∴． 12分 ‎20证明：（1）连接AE交BF于点N，连接MN．‎ 因为ABEF是正方形，所以N是AE的中点，‎ 又M是ED的中点，所以MN∥AD．‎ 因为AD⊄平面BFM，MN平面BFM，‎ 所以AD∥平面BFM．…………………6分 ‎（2）因为ABEF是正方形，所以BE⊥AB，‎ 因为平面ABEF⊥平面ABC，平面ABEF∩平面ABC=AB，‎ 所以BE⊥平面ABC，因为CD∥BE，所以取BC的中点O，‎ 连接OM，则OM⊥平面ABC，因为△ABC是正三角形，所以OA⊥BC，‎ 所以以O为坐标原点建立如图所示的空间直角坐标系：‎ 设CD=1，则B（0，1，0），E（0，1，2），D（0，﹣1，1），‎ ‎，．‎ 设平面BMF的一个法向量为，‎ 则，所以，‎ 令，则z=﹣6，y=﹣9，所以．‎ 又因为是平面BME的法向量，‎ 所以．‎ 所以二面角E﹣BM﹣F的余弦值为．…………………12分 ‎21试题解析：（1）由题意得：圆心到直线的距离为圆的半径，‎ 所以圆的标准方程为：所以圆心到直线的距离d=1‎ ‎…………………4分 ‎（2）因为点,所以,‎ 所以以点为圆心，线段长为半径的圆方程：（1）‎ 又圆方程为：（2），由得直线方程：…………………8分 ‎（3）设直线的方程为：联立得：，‎ 设直线与圆的交点，‎ 由，得，（3）‎ 因为为钝角，所以,‎ 即满足，且与不是反向共线，‎ 又，‎ 所以（4）‎ 由（3）（4）得，满足，即，‎ 当与反向共线时，直线过（1，-1），此时，不满足题意，‎ 故直线纵截距的取值范围是，且…………………12分 ‎22（1）设，代入，得．由题设得，解得（舍去）或，∴C的方程为；…………………3分 ‎（2）由题设知与坐标轴不垂直，故可设的方程为，代入得．设则 ‎．故的中点为．…………………6分 又的斜率为的方程为．将上式代入，并整理得．设则．故的中点为．…………………9分 由于垂直平分线，故四点在同一圆上等价于，从而 即，化简得，解得或．所求直线的方程为或．‎ ‎…………………12分