山西省忻州市岢岚县中学2019-2020学年高一上学期期中考试数学试卷 13页

数学期中测试卷 一、选择题（每小题 5 分，共 12 小题 60 分） 1. 若集合 , ,则 ( ) A. B. C. D. 2. 设集合 ， ，下面的对应关系 能构成从 到 的映射的是（ ） A. B. C. D. 3. 已知 ,则 的值是( ) A. B. C. D. 4. 已知函数 ,则 等于( ) A. B. C. D. 5. 如图所示的是定义域在区间 上的函数 的图像,则下列关于函数 的说法错误 的是( ) A. 函数在区间 上单调递增 B. 函数在区间 上单调递增 C. 函数在区间 上单调递增 D. 函数在区间 上不单调. 6. 已知函数 为奇函数,且当 时, ,则 等于( ) A. B. C. D. 7. 设 ,且 ,则 等于( ) A. B. C. D. 8. 已知函数 是幂函数,且在 是减函数,则 ( ) A. B. C. D. 9. 函数 在 上的最大值与最小值之和为 ,则函数 在 上的最大值与最小值 的差是 ( ) A. B. C. D. 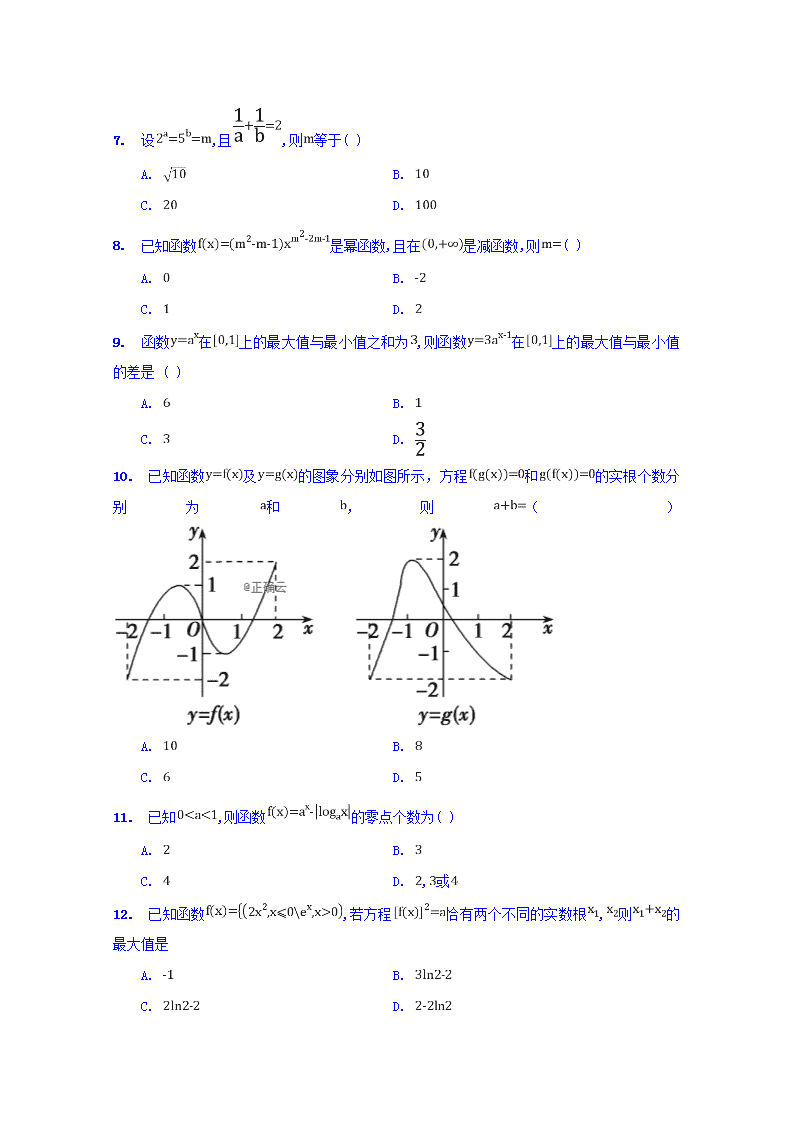10. 已知函数 及 的图象分别如图所示，方程 和 的实根个数分 别 为 和 ， 则 （ ） A. B. C. D. 11. 已知 ,则函数 的零点个数为( ) A. B. C. D. , 或 12. 已知函数 ,若方程 恰有两个不同的实数根 , 则 的 最大值是 A. B. C. D. 二、填空题（每小题 5 分，共 4 小题 20 分） 13. 已知函数 的图象经过点 ，则函数 的图象经过点__________． 14. 函数 的定义域为__________.（用区间形式表示） 15. 已知全集 , , , , 若 ,则 __________. 16. 化简： __________． 三、解答题（第 17 题 10 分，第 18 题 12 分，第 19 题 12 分，第 20 题 12 分，第 21 题 12 分， 第 22 题 12 分，共 6 小题 70 分） 17. 设 ．求： (1) ； (2) ． 18. 计算下列各式： （1） ； （2） . 19. 已知函数 ,其中 为常数,且函数 的图像过点 . (1)求 的值; (2)判断函 数 的奇偶性; (3)求证函数 在 上是单调递减函数. 20. 已知函数 . (1)若 ,求 ; (2)若 在 内存在零点,求 的取值 范围; (3)若 对 恒成立,求 的取值范围. 21. 已知 是定义在 上的偶函数,且当 时, . (1)求 的值; (2) 求 的解析式. 22. 已知函数 且 在 上的最大值与最小值之差为 . (1)求实数 的值; (2) 若 ,当 时,解不等式 . 数学期中测试卷 一、选择题（每小题 5 分，共 12 小题 60 分） 1. 若集合 , ,则 ( ) A. B. C. D. 【答案】B 【解析】 , ,∴ .故选:B. 2. 设集合 ， ，下面的对应关系 能构成从 到 的映射的是（ ） A. B. C. D. 【答案】B 【解析】A 中 ，D 中 .C 明显不符合，故选 B. 3. 已知 ,则 的值是( ) A. B. C. D. 【答案】A 【解析】依题意得 . 4. 已知函数 ,则 等于( ) A. B. C. D. 【答案】C 【解析】∵ ,∴ ,∴ . 5. 如图所示的是定义域在区间 上的函数 的图像,则下列关于函数 的说法错误 的是( ) A. 函数在区间 上单调递增 B. 函数在区间 上单调递增 C. 函数在区间 上单调递增 D. 函数在区间 上不单调. 【答案】C 【解析】当一个函数出现两个或两个以上的单调区间时不能用“ ”连接. 6. 已知函数 为奇函数,且当 时, ,则 等于( ) A. B. C. D. 【答案】A 【解析】由题 . 7. 设 ,且 ,则 等于( ) A. B. C. D. 【答案】A 【解析】∵ , ,∴ , ,且 ,∵ ,∴ ,∴ . 8. 已知函数 是幂函数,且在 是减函数,则 ( ) A. B. C. D. 【答案】D 【解析】∵函数 是幂函数, ∴ ,解得 或 , 当 时, 函数为 在区间 上单调递增,不满足条件. 当 时,函数为 在 上是递减 的,满足题意.故选 D. 9. 函数 在 上的最大值与最小值之和为 ,则函数 在 上的最大值与最小值 的差是 ( ) A. B. C. D. 【答案】D 【解析】∵函数 在 上的最大值与最小值之和为 ,∴ ,解得 . ∴函数 在 上的最大值是 ,最小值是 ;∴最大值与最小值的差是 . 10. 已知函数 及 的图象分别如图所示，方程 和 的实根个数分 别 为 和 ， 则 （ ） A. B. C. D. 【答案】A 【解析】由图象知， 有 个根，分别为 ， （ ），其中 ； 有 个根， ， ，由 ，得 或 ， 由图象可知当 所对应的值为 ， 时， 其都有 个根，因而 ； 由 ，知 或 ， 由图象可以看出当 时，有 个根， 而当 时，有 个根，即 . 所以 . 11. 已知 ,则函数 的零点个数为( ) A. B. C. D. , 或 【答案】A 【解析】函数 的零点个数,等于函数 和函数 的图象的交点个数.如 图所示,数形结合可得,函数 和函数 的图象的交点个数为 , 故 时,函数 的零点个数为 ,故选 A. 12. 已知函数 ,若方程 恰有两个不同的实数根 , 则 的 最大值是 A. B. C. D. 【答案】B 【解析】作出 的函数图像如图所示: 由 可得 ,由 已知方程 恰有两个不同的实数根,∴ ,即 . 不妨设 ,则 , 令 ,则 , ,∴ ,令 ,则 ,∴当 时, ,当 时, , ∴当 时, 取得最大值 . 二、填空题（每小题 5 分，共 4 小题 20 分） 13. 已知函数 的图象经过点 ，则函数 的图象经过点__________． 【答案】 . 【解析】因为 ，令 ，则 过点 ，所以 过点 . 14. 函数 的定义域为__________.（用区间形式表示） 【答案】 【解析】要使函数式有意义，需 ，即 且 ， 所以函数 的定义域为 . 15. 已知全集 , , , , 若 ,则 __________. 【答案】 【解析】 , ,由题意知 ,所以 . 16. 化简： __________． 【答案】 【解析】原式 ． 三、解答题（第 17 题 10 分，第 18 题 12 分，第 19 题 12 分，第 20 题 12 分，第 21 题 12 分， 第 22 题 12 分，共 6 小题 70 分） 17. 设 ．求： (1) ； (2) ． 【答案】(1) ； (2) . 【解析】由题意可得 ． (1) ， ； (2) ， . 18. 计算下列各式： （1） ； （2） . 【答案】略 【解析】（1） . （2） 原式 . 19. 已知函数 ,其中 为常数,且函数 的图像过点 . (1)求 的值; (2)判断函 数 的奇偶性; (3)求证函数 在 上是单调递减函数. 【答案】见解析 【解析】(1)∵函数 的图像过点 ,∴ ,∴ . (2)由(1)知 ,又 ,所以 ,其定义域为 , ,所以 为奇函数. (3) 证明:设 ,且 ,则 ,∵ ,∴ , , ,∴ ,∴函数 在 上是单调递减函数. 20. 已知函数 . (1)若 ,求 ; (2)若 在 内存在零点,求 的取值 范围; (3)若 对 恒成立,求 的取值范围. 【答案】见解析 【解析】(1)函数 . 由于 ,所以 ,解得 . 所以 . 故 , ,即 . (2) 在 内存在零点,且函数 在 上递增, 所以 ,即 , 解得 ,即 . (3)由于 , 即 , 即 对 恒成立, 所以 , 解得 ,由最初的解析式知 ， 所以 的取值范围是 . 21. 已知 是定义在 上的偶函数,且当 时, . (1)求 的值; (2) 求 的解析式. 【答案】(1) ; (2) . 【解析】本题考查函数的性质的应用. (1)∵ , ,∴ . (2)设 ,则 , , 故 . 22. 已知函数 且 在 上的最大值与最小值之差为 . (1)求实数 的值; (2) 若 ,当 时,解不等式 . 【答案】见解析; 【解析】(1)当 时, , ,则 ,解得 ; 当 时, , ,则 ,解得 , 综上得 或 ; (2)当 时,由(1)知 , 为奇函 数且在 上是增函数, ∴ 或 ,所以不等式 的解集为 .