河南省三门峡市外国语高级中学2020届高三模拟考试数学试卷1 16页

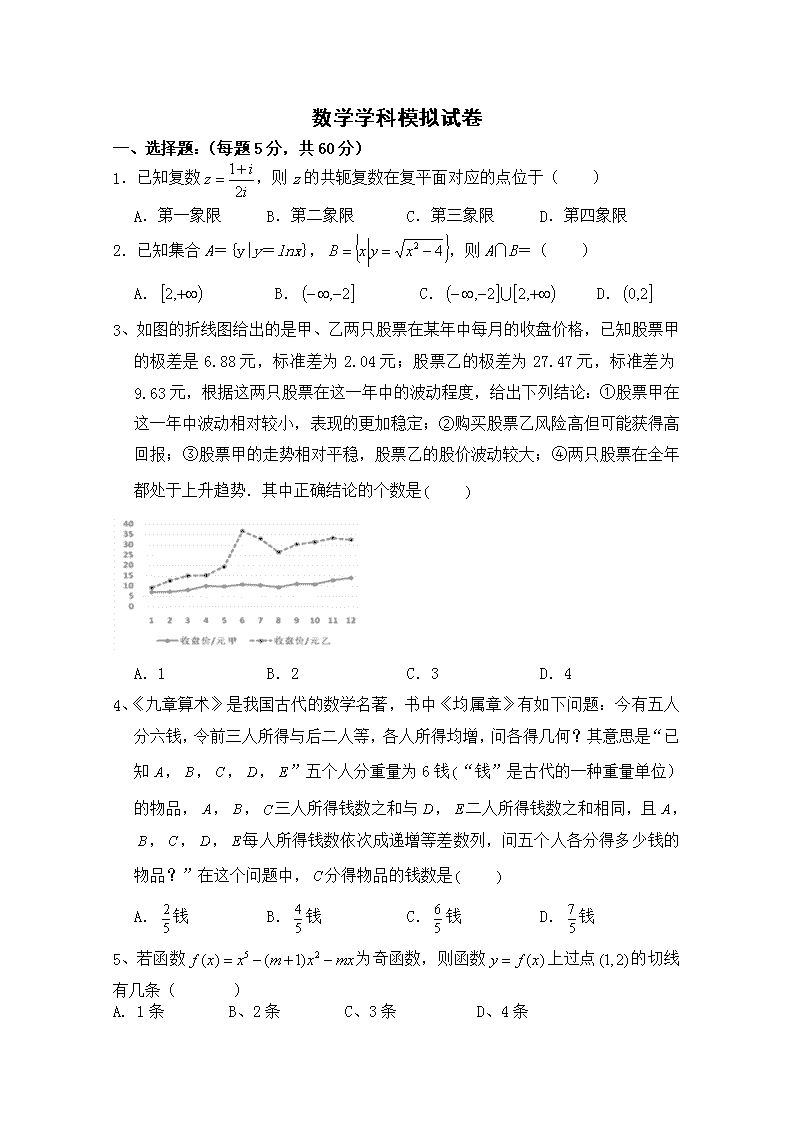
数学学科模拟试卷 一、选择题：（每题5分，共60分）‎ ‎1．已知复数，则z的共轭复数在复平面对应的点位于（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2．已知集合A＝{y|y＝lnx}，，则A∩B＝（　　）‎ A． B． C． D．‎ ‎3、如图的折线图给出的是甲、乙两只股票在某年中每月的收盘价格，已知股票甲的极差是6.88元，标准差为2.04元；股票乙的极差为27.47元，标准差为9.63元，根据这两只股票在这一年中的波动程度，给出下列结论：①股票甲在这一年中波动相对较小，表现的更加稳定；②购买股票乙风险高但可能获得高回报； ③股票甲的走势相对平稳，股票乙的股价波动较大； ④两只股票在全年都处于上升趋势．其中正确结论的个数是　　‎ A．1 B．‎2 ‎C．3 D．4‎ ‎4、《九章算术》是我国古代的数学名著，书中《均属章》有如下问题：今有五人分六钱，令前三人所得与后二人等，各人所得均增，问各得几何？其意思是“已知，，，，”五个人分重量为6钱“钱”是古代的一种重量单位）的物品，，，三人所得钱数之和与，二人所得钱数之和相同，且，，，，每人所得钱数依次成递增等差数列，问五个人各分得多少钱的物品？”在这个问题中，分得物品的钱数是　　‎ A．钱 B．钱 C．钱 D．钱 5、 若函数为奇函数，则函数上过点的切线有几条（ ）‎ A. ‎1条 B、2条 C、3条 D、4条 5、 在三棱锥中，分别为棱上靠近的三等分点，则（ ）‎ A、 ‎ B、 C、 D、 ‎ ‎7、设某几何体的三视图如右图（尺寸的长度单位为m）。 ‎ ‎ 则该几何体的体积为（ ） ‎ A．2 B． ‎3 ‎ C． 4 D．5‎ ‎8、点在直线上，若存在过的直线交抛物线于两点，且 ‎，则称点为“等点”，那么下列结论中正确的是 （ ）‎ ‎ A．直线上的所有点都是“等点”‎ ‎ B．直线上仅有有限个点是“等点”‎ ‎ C．直线上的所有点都不是“等点”‎ ‎ D．直线上有无穷多个点（点不是所有的点）是“等点”‎ ‎9.已知函数，若方程恰有四个不同的实数根，则实数的取值范围是　　‎ A． B． C． D．‎ ‎10．如图，圆、圆、圆内切于正三角形中且彼此相外切，在三角形内随机取一点，则此点取自三角形（阴影部分）的概率是　　‎ A． ‎ B． ‎ C． D．‎ ‎11、已知 , 分别是双曲线 的左右焦点，若 关于渐近线的对称点恰落在以为圆心， OF2长度为半径的圆上，则双曲线C的离心率为（ ）‎ A.3 B. C.2 D.‎ ‎ 12.设数列 的各项都为正数且 =1， 内的点 均满足 与 ‎ 的面积比为2:1,若 ，则 的值为（ ）‎ A.15 B‎.17 C.29 D.32‎ 二、填空题：（每题5分，共20分）‎ ‎14．已知数列{an}满足a1＝，an+1﹣an＝2n+1，则数列的前n项和Sn＝　 　．‎ ‎15．有7名学生，其中有3名会唱歌，3名会跳舞，1名既会唱歌也会跳舞，现从中选出2名会唱歌的，1名会跳舞的去参加文艺演出，则共有选法　 　种．‎ ‎16．设△ABC的内角A，B，C所对的边分别为a，b，c，且，，则tan2B•tan‎3A的最大值为　 　‎ ‎ 三、解答题：(共70分，解答应写出文字说明，证明过程或演算步骤．）‎ ‎17、（本小题满分12分）‎ ‎17．如图在四边形中，，，，，．（1）求长；（2）求．‎ ‎18、如图，平面平面，是以为斜边的等腰直角三角形，分别为，，的中点，，．‎ ‎ （I）设是的中点，证明：平面；‎ ‎ （II）证明：在内存在一点，使平面，并求点到，的距离．‎ ‎19、（本小题满分12分）‎ 设椭圆的上焦点为，过的直线与交于,两点，点的坐标为．‎ ‎(1)当与轴垂直时，求直线的方程；‎ ‎(2)设为坐标原点，证明：．‎ ‎20、（本小题满分12分）‎ 某公司订购了一批树苗，为了检测这批树苗是否合格，从中随机抽测100株树苗的高度，经数据处理得到如图的频率分布直方图，其中最高的16株的茎叶图如图所示．以这100株树苗高度的频率．‎ ‎（1）求这批树苗的高度高于1.60米的概率，并求图中，，的值；‎ ‎（2）若从这批树苗中随机选取3株，记为高度在，的树苗数量，求的分布列和数学期望；‎ ‎（3）若变量满足且，则称变量满足近似于正态分布的概率分布，如果这批树苗的高度满足近似于正态分布 的概率分布，则认为这批树苗是合格的，将顺利获得签收，否则，公司将拒绝签收，试问，该批树苗能否被签收？‎ ‎21、（本小题满分12分）‎ ‎21．已知函数f（x）＝-ax+a+lnx， ．‎ ‎（Ⅰ）讨论f（x）的单调性；‎ ‎（Ⅱ）若f（x）0恒成立，求a的取值范围．‎ ‎（III）在（Ⅱ）的条件下，证明：‎ 选做题 请考生在第22、23、两题中任选一题作答，如果多做，则按所做的第一题记分，答时用2B铅笔在答题卡上把所选题目的题号涂黑 ‎22．（本小题满分10分）选修4-4：坐标系与参数方程 以平面直角坐标系 xOy的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位，已知曲线C：（θ为参数），直线：，直线的极坐标方程为 ‎（Ⅰ）求曲线C和直线的普通方程；‎ ‎（Ⅱ）与C交于不同两点M，N，MN的中点为P，与的交点为Q，恒过点A，求|AP|•|AQ|的值．‎ ‎23. （本小题满分10分）选修4-5：不等式选讲 函数，.‎ ‎（Ⅰ）若求不等式的解集 ‎（Ⅱ）若不等式的解集非空，求的取值范围 参考答案 ‎1．解：根据题意，复数，‎ 则其共轭复数，其对应的点为（﹣1，﹣1），位于第一象限；‎ 故选：A．‎ ‎2．解：由A中的函数y＝lnx，得到A＝；‎ 由B中的不等式变形得：，即B＝‎ 则A∩B＝‎ 故选：C．‎ ‎3、解：①甲的标准差2.04，乙的标准差为9.63，则甲的标准差小，‎ 即股票甲在这一年中波动相对较小，表现的更加稳定，故①正确，‎ ‎②股票甲的极差是6.88元，股票乙的极差为27.47元，‎ 则购买股票乙风险高但可能获得高回报；故②正确，‎ ‎③由图象知股票甲的走势相对平稳，股票乙的股价波动较大，故③正确，‎ ‎④甲股票在6到8月份之间出现下跌，故④错误，‎ 故正确的是①②③． 故选：．‎ ‎4、解：设，，，，五个人所得钱数依次为，，，，，‎ 由题意得，解得，，‎ 分得物品的钱数是（钱．故选：．‎ ‎5：B 6：A ‎7、这是一个三棱锥,高为2,底面三角形一边为4,这边上的高为3, 体积等于×2×4×3＝4‎ ‎ 8、本题采作数形结合法易于求解，如图，‎ 设，‎ 则，‎ ‎∵，‎ ‎∴‎ ‎（第8题解答图）‎ 消去n,整理得关于x的方程 （1）‎ ‎∵恒成立，‎ ‎∴方程（1）恒有实数解，∴应选A.‎ ‎9.解：函数，若方程恰有四个不同的实数根，‎ 即，有4个不同的交点，‎ 分别画出，与的图象，‎ 当时，，‎ ‎，‎ 设直线与相切于点，，‎ ‎，‎ ‎，，‎ ‎，，‎ 当时，，‎ ‎，‎ 设直线与相切于点，，‎ ‎，‎ ‎，，‎ ‎，，‎ 结合图象可知，‎ 故选：．（本题还可以用参变分离）‎ ‎10.解：如图，设一个内切圆的半径为，则，‎ 则，，‎ 因为正三角形与正三角形相似，‎ 则在正三角形内随机取一点，则此点取自三角形（阴影部分）的概率是：‎ ‎．‎ 故选：．‎ ‎11解:由题意 一条渐近线方程为 则到渐近线的距离为 ‎ 设关于渐近线的对称点为M,与渐近线交于A,‎ 则，A为的中点, 又0是的中点,则OA//,为直角, 为直角三角形, 由勾股定理得 ,, ,. 所以C选项是正确的.‎ 12、 A 12、 ‎ ‎ ‎14解：∵an+1﹣an＝2n+1，∴n≥2时，an﹣an﹣1＝2n﹣1．‎ ‎∴an＝（an﹣an﹣1）+（an﹣1﹣an﹣2）+…+（a2﹣a1）+a1‎ ‎＝（2n﹣1）+（2n﹣3）+…+（2×2﹣1）+‎ ‎＝+＝n2﹣．‎ ‎∴＝＝．‎ ‎∴数列{}的前n项和Sn＝2+…+‎ ‎＝2‎ ‎＝．‎ ‎15、解：4名会唱歌的从中选出两个有C42＝6（种），‎ ‎4名会跳舞的选出1名有4种选法，‎ 但其中一名既会唱歌又会跳舞的有一个，‎ 两组不能同时用他，‎ ‎∴共有4x6﹣3＝21种 故答案为：21．‎ ‎16、解：∵acosB﹣bcosA＝c，‎ ‎∴2RsinAcosB﹣2RsinBcosA＝2RsinC，‎ ‎∴sinAcosB﹣sinBcosA＝sinC，‎ ‎∴sinAcosB﹣sinBcosA＝sin（A+B），‎ ‎∴sinAcosB﹣sinBcosA＝（sinAcosB+sinBcosA），‎ ‎∴2sinAcosB＝8sinBcosA，‎ ‎∴tanA＝4tanB，‎ ‎∵，‎ ‎∴tanB＞1，‎ ‎∴tan2B•tan3A＝•tan3A＝，‎ 令x＝tan2B，则t＞1，‎ y＝，则y′＝，‎ 当1＜t＜2时，y′＞0，y＝为增函数，‎ 当t＞2时，y′＜0，y＝为减函数，‎ 故当t＝2时，y＝取最大值﹣512，‎ 故答案为：﹣512．‎ ‎17、解：（1）在中，，，，‎ 又，，为为 等腰三角形，‎ 由余弦定理可得，‎ 中，，，‎ ‎，由正弦定理可得．‎ ‎（2）在中，，，，‎ 根据余弦定理可得．‎ 所以在中，根据余弦定理可得 ‎18、证明：（I）如图，连结OP，以O为坐标原点，分别以OB、OC、OP所在直线为轴，轴，轴，建立空间直角坐标系O，. ‎ 则，由题意得，因，因此平面BOE的法向量为，得，又直线不在平面内，因此有平面 ‎（II）设点M的坐标为，则，因为 平面BOE，所以有，因此有，即点M的坐标为，在平面直角坐标系中，的内部区域满足不等式组，经检验，点M的坐标满足上述不等式组，所以在内存在一点，使平面，由点M的坐标得点到，的距离为．. ‎ ‎19:【解析】(1)由已知得，的方程为．‎ 由已知可得，点的坐标为或．‎ 所以的方程为或．‎ ‎(2)由角平分线定理知，要证只需证。‎ 当与轴垂直时，．‎ 当与轴平行时，为的垂直平分线，所以。‎ 当与轴不重合也不垂直时，设的方程为，，‎ 则，，直线，的斜率之和为．‎ 由，得 ‎．‎ 将代入得 ‎．‎ 所以，，．‎ 则．‎ 从而，故，的倾斜角互补，所以．‎ 综上，，即。‎ ‎20、解：（1）由茎叶图可知，100株样本树苗中高度高于1.60的共有15株，‎ 以样本的频率估计总体的概率，可得这批树苗的高度高于1.60的概率为0.15．‎ 记为树苗的高度，结合频率分布直方图，可得：‎ ‎，‎ ‎，‎ ‎，‎ 又由于组距为0.1，所以，，．‎ ‎（2）以样本的频率估计总体的概率，可得：‎ 从这批树苗中随机选取1株，高度在，的概率：‎ ‎．‎ 因为从这批树苗中随机选取3株，相当于三次重复独立试验，‎ 所以随机变量服从二项分布，‎ 故的分布列为：，1，2，，（8分）‎ 的分布列为：‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎0.027‎ ‎0.189‎ ‎0.441‎ ‎0.343‎ ‎．‎ ‎（3）由，取，，‎ 由（2）可知，，‎ 又结合（1），可得：‎ ‎，‎ 所以这批树苗的高度满足近似于正态分布的概率分布，‎ 应认为这批树苗是合格的，将顺利获得该公司签收．‎ ‎21、解：（Ⅰ）函数的定义域为（0，+∞），‎ 函数的导数f′（x），‎ 若a≤0，则f′（x）0，此时函数在（0，+∞）上递增，‎ 若a＞0，则当，f′（x）>0，此时函数单调递增.‎ ‎ 时，f′（x）<0，此时函数单调递减.‎ ‎（Ⅱ）由（Ⅰ）知a≤0，则f′（x）>0，函数f（x）在（0，+∞）上递增，‎ ‎∵f（1）＝0，∴f（x）>=0不恒成立，‎ 若0＜a＜1，当x∈（1，）时，f（x）单调递增，f（x）>f（1）＝0，不合题意，‎ 若a＞1，当x∈（，1）时，f（x）单调递减，f（x）>f（1）＝0，不合题意，‎ 若a＝1，当x∈（0，1）上单调递增，f（x）在（1，+∞）单调递减，f（x）f（1）＝0，符合题意，‎ 故a＝1时，且lnx≤x﹣1，（当且仅当x＝1时取等号）.‎ ‎（III）‎ 当 当 两式相乘，即得 ‎22．（本小题10分）‎ ‎【解析】‎ ‎（Ⅰ）曲线C：（θ为参数），‎ 化普通方程为；‎ ‎：化普通方程为x﹣2y﹣4=0； --------------4分 ‎（Ⅱ）因为恒过点A，所以可设的参数方程为：‎ ‎（为参数），代入圆C方程，整理得 ‎，---------------6分 因为M，N，P，Q，都在上，所以可设它们对应的参数依次为，，，，‎ 所以 ，‎ 又P为MN的中点，所以 的参数方程代入的方程，可得，‎ 所以 所以 |AP|•|AQ|=10．-------------------------10分 ‎23. （本小题10分）‎ ‎【解析】‎ ‎（Ⅰ）当时，，即 上述不等式可化为：‎ ‎，或，或 解得 ‎ 所以解集为 ---------------4分 ‎（Ⅱ）令，因为，所以 ‎， -------------------6分 所以 ‎ 当时，；‎ 当时，；‎ 当时，，‎ 所以函数的值域为，‎ 因为不等式的解集非空，‎ 所以 ，‎ 所以 .---------------------10分