高考数学专题复习：《空间几何体的表面积与体积》同步测试题 7页

‎《空间几何体的表面积与体积》同步测试题 一、选择题 ‎1、一个球与它的外切圆柱、外切等边圆锥（圆锥的轴截面为正三角形）的体积之比（ ）‎ A．2：3：5 B．2：3：‎4 ‎ C．3：5：8 D．4：6：9‎ ‎2、直径为‎10cm的一个大金属球，熔化后铸成若干个直径为‎2cm的削球，如果不计损耗，可铸成这样的小球的个数为 （ ）‎ A．5 B．‎15 ‎ C．25 D．125‎ ‎3、与正方体各面都相切的球，它的表面积与正方体的表面积之比为 （ ）‎ A． B． C． D．‎ ‎4、直三棱柱各侧棱和底面边长均为a，点D是CC′上任意一点，连结A′B，BD，A′D，AD，则三棱锥A—A′BD的体积 （ ）‎ ‎ A． B． C． D．‎ ‎5、将一个边长为a的正方体，切成27个全等的小正方体，则表面积增加了 （ ）‎ ‎ A． B．‎12a2 ‎C．‎18a2 D．‎24a2‎ ‎6、球的体积与其表面积的数值相等，则球的半径等于 （ ）‎ A． B．‎1 ‎ C．2 D．3‎ ‎7、若正棱锥底面边长与侧棱长相等，则该棱锥一定不是 （ ）‎ ‎ A．三棱锥 B．四棱锥 C．五棱锥 D．六棱锥 ‎ ‎8、过正三棱柱底面一边的截面是 （ ）‎ A．三角形 B．三角形或梯形 C．不是梯形的四边形 D．梯形 ‎9、中心角为135°的扇形，其面积为B，其围成的圆锥的全面积为A，则A：B为（ ）‎ ‎ A．11：8 B．3：‎8 ‎ C．8：3 D．13：8‎ ‎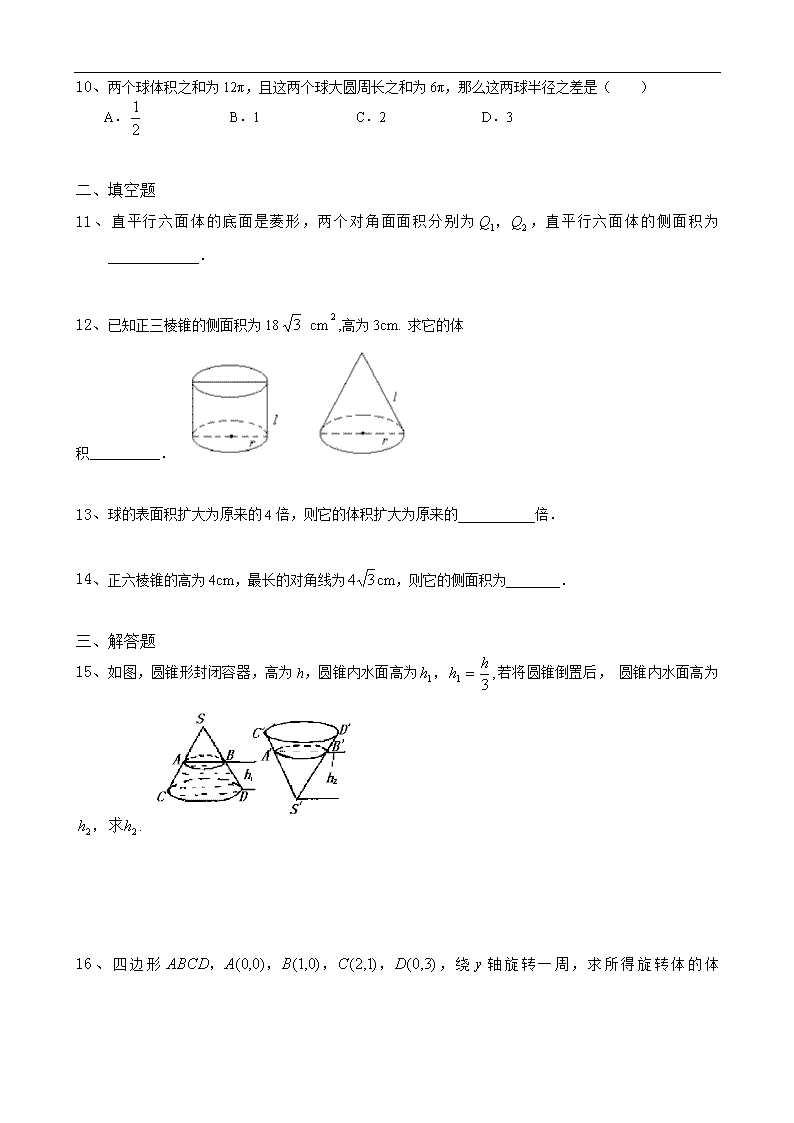10、两个球体积之和为12π，且这两个球大圆周长之和为6π，那么这两球半径之差是（ ）‎ ‎ A． B．‎1 ‎ C．2 D．3‎ 二、填空题 ‎11、直平行六面体的底面是菱形，两个对角面面积分别为，直平行六面体的侧面积为_____________．‎ ‎12、已知正三棱锥的侧面积为‎18 cm,高为3cm. 求它的体积 ．‎‎ ‎ ‎13、球的表面积扩大为原来的4倍，则它的体积扩大为原来的___________倍．‎ ‎14、正六棱锥的高为‎4cm，最长的对角线为cm，则它的侧面积为_________．‎ 三、解答题 ‎15、如图，圆锥形封闭容器，高为h，圆锥内水面高为若将圆锥倒置后， 圆锥内水面高为‎ ‎ ‎16、四边形，绕y 轴旋转一周，求所得旋转体的体积．‎‎ ‎ ‎17、如图，‎ ‎ 三棱柱 上一点，求 ．‎ ‎18、如图，在正四棱台内，以小底为底面。大底面中心为顶点作一内接棱锥. 已知棱台小底面边长为b，大底面边长为a，并且棱台的侧面积与内接棱锥的侧面面积相等，求这个棱锥的高，并指出有解的条件．‎ ‎19、（14分）已知：一个圆锥的底面半径为R，高为H，在其中有一个高为x的内接圆柱．‎ ‎ （1）求圆柱的侧面积；‎ ‎ （2）x为何值时，圆柱的侧面积最大．‎ ‎20、①轴截面是正方形的圆柱叫等边圆柱．已知：等边圆柱的底面半径为r，求：全面积；‎ ‎ ②轴截面是正三角形的圆锥叫等边圆锥.已知：等边圆锥底面半径为r，求：全面积．‎ 四、选择题 ‎21、下列命题正确的是（　　）‎ Ａ．经过三点确定一个平面 Ｂ．经过一条直线和一个点确定一个平面 Ｃ．四边形确定一个平面 Ｄ．两两相交且不共点的三条直线确定一个平面 以下是答案 一、选择题 ‎1、D ‎2、D ‎3、B ‎4、C ‎ ‎5、B ‎6、D ‎7、D ‎8、B ‎9、A ‎10、B 二、填空题 ‎11、； ‎ ‎12、cm3.‎ ‎13、8； ‎ ‎14、 cm； ‎ 三、解答题 ‎15、分析：圆锥正置与倒置时，水的体积不变，另外水面是平行于底面的平面，此平面截得的小圆锥与原圆锥成相似体，它们的体积之比为对应高的立方比.‎ ‎ 解： ‎ ‎ ‎ ‎ 小结：此题若用 计算是比较麻烦的，因为台体的上底面半径还需用导出来，我们用 的体积之间有比例关系，可以直接求出.‎ ‎16、解：‎ ‎ ‎ ‎ ‎ ‎17、解法一：设 的距离为 ‎ ‎ 把三棱柱 为相邻侧面的平行六面体，此平行六面体体积为原三棱柱体积的两倍.‎ ‎ ‎ ‎ 解法二： ‎ ‎ ‎ ‎ ‎ ‎ 小结：把三棱柱接补成平行六面体是重要的变换方法，平行六面体的每一个面都可以当作柱体的底，有利于体积变换.‎ ‎18、分析：这是一个棱台与棱锥的组合体问题，也是立体几何常见的问题，这类问题的图形往往比较复杂，要认真分析各有关量的位置和大小关系，因为它们的各量之间的关系较密切，所以常引入方程、函数的知识去解.‎ ‎ 解：如图，过高的中点E作棱锥和棱台的截面，得棱台的斜高EE1和棱锥的斜高为EO1，设，所以 ‎ ‎ ‎ ①式两边平方，把②代入得：‎ ‎ ‎ ‎ 显然，由于，所以此题当且仅当时才有解.‎ ‎ ‎ 小结：在棱台的问题中，如果与棱台的斜高有关，则常应用通过高和斜高的截面，如果和棱台的侧棱有关，则需要应用通过侧棱和高的截面，要熟悉这些截面中直角梯形的各元素，进而将这些元素归结为直角三角形的各元素间的运算，这是解棱台计算问题的基本技能之一.‎ ‎19、解：（1）设内接圆柱底面半径为r. ‎ ‎ ‎ ‎ ②代入①‎ ‎ ‎ ‎ （2）‎ ‎ ‎ ‎20、①解：‎ ‎ ‎ ‎ ②解：‎ ‎ ‎ 四、选择题 ‎21、答案：Ｄ．‎